
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методические указания по изучению механики грунтовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Учебное пособие для студентов заочной формы обучения строительных специальностей
Санкт-Петербург – 2011 Оглавление
1. Программа дисциплины «Механика грунтов» и рекомендуемая литература
1. Предмет и задачи механики грунтов, связь с другими дисциплинами. 2. Виды грунтов. Характеристики состава и состояния грунтов, классификации по ним. Условное расчетное сопротивление грунта. Структура, текстура, структурные связи в грунтах. Виды воды в грунтах. Закон фильтрации. Структурно-неустойчивые грунты. 3. Напряженно-деформированное состояние (НДС) грунтов. Виды НДС грунта в основаниях. Особенности деформирования грунта, стадии деформирования. Деформативные характеристики. 4. Компрессионное сжатие. Закономерность уплотнения. Определение коэффициента сжимаемости и модуля деформации в условиях компрессионного сжатия. Другие методы определения деформативных характеристик. 5. Прочность грунтов. Закон Кулона. Условие предельного равновесия. Прочностные характеристики, их определение. 6. Определение напряжений в грунтах от различных нагрузок. Напряжения от собственного веса грунта. 7. Деформации грунтов. Методы расчета стабилизированных осадок. 8. Критические давления на основания. Определения первого критического давления, расчетного сопротивления основания и второго критического давления или предельной нагрузки. 9. Устойчивость откосов. Откос, сложенный несвязным грунтом. Предельная высота вертикального откоса. Расчет устойчивости откосов по способу круглоцилиндрических поверхностей скольжения. 10. Давление грунтов на ограждения и подпорные стенки. Виды давления. Определение давления на гладкую вертикальную подпорную стенку с горизонтальной поверхностью засыпки (эпюры, формулы).
Рекомендуемая литература Основная 1. Механика грунтов, основания и фундаменты. Учебное пособие для вузов. Под редакцией С.Б. Ухова. М.: АВС, 1997. 2. Швецов Г.И. Инженерная геология, механика грунтов, основания и фундаменты: Учебник для вузов. - М.: Высш. шк,, 1997. 3. Далматов Б.И. и др. Механика грунтов. Ч. 1. Основы геотехники в строительстве. – М.: Изд-во АСВ; СПб.: СПбГАСУ, 2000.
Дополнительная 1. ГОСТ 25100-95. Грунты. Классификация 2. Далматов Б.И. Механика грунтов, основания и фундаменты: Учебник для вузов. – М.: Стройиздат, 1981. Методические указания по изучению механики грунтов
При самостоятельном изучении дисциплины следует использовать краткий конспект лекций, помещенный в данном учебном пособии, а также разделы по механике грунтов учебников, имеющихся в библиотеке СПбГАУ [1, 2]. По отдельным темам приведенной выше программы полезно учесть следующее. Темы 1, 2. Механика грунтов тесно связана прежде всего с инженерной геологией, изучающей грунты как природные образования. Механика грунтов дает возможность описания механического поведения грунтов, их сжимаемости и прочности. Это возможно только на базе всестороннего учета природы и физических свойств грунтов, изученных ранее в разделе инженерной геологии «Грунтоведение». Темы 3–5 дают основные закономерности сжимаемости и прочности грунтов, установленные экспериментально и обобщением опыта строительства. В них проявляется связь механики грунтов с фундаментальными механическими дисциплинами: теоретической механикой и механикой деформируемого твердого тела. Используются условия равновесия, разложение сил, понятия деформаций и напряжений, круги Мора и др. В дополнение к материалу указанных тем, требуется знание методов определения физико-механических показателей грунтов. Это достигается сознательным выполнением лабораторных работ в учебной лаборатории. В конспекте лекций техника испытаний не рассматривается. Темы 6,7 посвящены определению напряжений в грунтах и расчету осадок. Грунт при этом рассматривается как линейно-деформируемая среда. Поэтому для определения напряжений используются решения теории сплошных тел. Но непосредственное использование этих же решений для расчета осадок оснований фундаментов возможно только в редких случаях. Чаще применяются приближенные инженерные методы – как, например, рассмотренный в конспекте метод послойного суммирования с условным ограничением сжимаемой толщи. Темы 8–10. Теория предельного напряженного состояния грунтов (или теория предельного равновесия) широко используется для определения предельных нагрузок на основания, при анализе устойчивости разнообразных взаимодействующих с грунтом конструкций (анкера, сваи, ограждения и т.д.) и массивов грунта. В прилагаемом конспекте материал по этим темам дан в минимальном для понимания объеме.
Конспект лекций по механике грунтов Основные виды грунтов, их характеристика и физические свойства Состав грунтов. Закон фильтрации. Структура и Структурные связи в грунтах
Наиболее сложными по своим свойствам являются дисперсные (раздробленные) грунты. Обычно они содержат три составные части (фазы) – минеральную (твердые частицы), жидкую (вода) и газообразную (воздух, водяной пар, другие газы). Мерзлые грунты содержат также лед. Полностью водонасыщенный грунт считают двухфазной системой (грунтовая масса). В дисперсных грунтах выделяют прочносвязанную (гигроскопическая), рыхлосвязанную (пленочная) и свободную (гравитационная и капиллярная) воду. Связанная вода существенно влияет на свойства глинистых грунтов и практически отсутствует в песчаных. Перемещение пленочной воды называется миграцией. Гравитационная вода перемещается (фильтрует) во всех грунтах под действием разности напоров. Для большинства грунтов выполняется закон ламинарной фильтрации Дарси в виде
где J = H/ℓ - гидравлический градиент; Кф – коэффициент фильтрации Из (1.1) К ф - это скорость фильтрации при J =1. В плотных глинистых грунтах фильтрация затрудняется оболочками связанной воды; считают, что фильтрация в них начинается лишь по достижении некоторого начального градиента напора J n. Уравнение (1.1) при этом принимает вид: Значения К ф и J n определяются экспериментально. Капиллярная вода удерживается в порах грунта за счет сил поверхностного натяжения. Высота капиллярного поднятия в грунтах растет с дисперсностью, составляя от 3…5 см в крупных песках до нескольких метров в глинистых грунтах. Под структурой понимаются размеры, форма, характер поверхности минеральных частиц грунта и характер связей между ними. Последние называются структурными связями и определяют прочность связных грунтов. В пылевато-глинистых грунтах различают структурные связи: 1) Водно-коллоидные, зависящие от сил электромолекулярного взаимодействия между поверхностями твердых частиц и их водными оболочками. Эти связи пластичны и обратимы. 2) Кристаллизационные связи, возникающие вследствие кристаллизации на поверхности частиц различных соединений из поровых растров. Это связи хрупкого типа и они практически необратимы. И классификации по ним
В механике грунтов используются следующие основные физические характеристики, определяемые опытным путем: – плотность грунта – плотность частиц грунта – влажность где m - масса в некотором объеме грунта V; ms и V s – масса и объем твердых частиц в некотором объеме грунта V; m wи V w – масса и объем воды в некотором объеме грунта V. По эти характеристикам рассчитывают производные показатели: - плотность сухого грунта – пористость где – коэффициент пористости
– степень влажности: где В расчетах часто используются не плотности, а удельные веса, рассчитываемые умножением плотности на ускорение свободного падения. Соответственно имеем удельный вес грунта
Например, если Если принять объем грунта Тогда объем твердых частиц
Грунт, залегающий ниже уровня подземных вод, испытывает взвешивающее действие воды. При этом вес твердых частиц уменьшается на вес вытесненной ими воды, т.е. на величину Для большинства грунтов значение Для глинистых грунтов наряду с влажностью важным является понятие консистенции, характеризующее степень подвижности грунта. Консистенция может быть твердой, пластичной и текучей. Влажности, соответствующие границам между этими состояниями, называются пределами пластичности или раскатывания WP (граница между твердым и пластичным состояниями) и текучести WL (между пластичным и текучим). Разность этих пределов называется числом пластичности Число пластичности тесно связано с содержанием в грунте глинистой фракции и поэтому используется в классификации: JP ≤ 0,07 - супесь, 0,07 < JP ≤ 0,17 - суглинок; JP > 0,17 – глина. Состояние грунта удобно характеризовать показателем текучести
Из (1.4) видно, что при
Для супесей, у которых число пластичности мало, во всем интервале Для песчаных грунтов очень важно состояние по плотности сложения: плотное, средней плотности, рыхлое. В последнем состоянии грунт дает большие деформации, особенно при динамических воздействиях. Имеющиеся опытные данные по отдельным разновидностям песчаных грунтов позволяют установить состояние по плотности с помощью табл. 1.1. Более объективно плотность сложения по значению Таблица 1.1
При 0< Наиболее надежно плотность устанавливается статическим или динамическим зондированием. Для песчаных грунтов, особенно мелких и пылеватых, на строительные свойства влияет коэффициент водонасыщения По характеристикам физического состава и состояния можно определить условное расчетное сопротивление грунта Для песчаных грунтов достаточно знать полное наименование грунта и плотность (табл. 1.2), а для пылевато-глинистых – название, значения Таблица 1.2 Таблица 1.3 Прочностные характеристики
Пусть проведено испытание на трехосное сжатие нескольких образцов одного и того же грунта, и образцы доведены до разрушения. Для каждого образца получена пара значений σ2i, σ1прi. Результаты испытаний можно представить в виде кругов Мора для напряжений (рис. 2.5). Опыты показывают, что в значительном интервале напряжений огибающая касательная к кругам имеет вид прямой с уравнением:
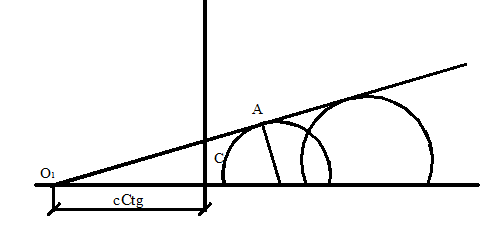
где φ и с – параметры линейной огибающей. Они имеют названия: φ – угол внутреннего трения; с – сцепление грунта. Это прочностные характеристики грунта. Уравнение (2.14) можно записать и через главные напряжения. Продолжим огибающую влево до σ и рассмотрим прямоугольный Δ О1АВ. Имеем АВ/О1В = Sinφ; (2.15)
Подставляя значения АВ и О1В в (2.15), получаем условие прочности в главных напряжениях:
Для несвязных грунтов (пески) с ≈ 0 и условие (2.16) упрощается:
Характер разрушения образца при испытании в стабилометре зависит от вида и состояния грунта. Наиболее четкая картина в виде скола имеет место для песков плотных и средней плотности и прочных глинистых грунтов, причем плоскость скола, на которой действует τmax , наклонена к вертикали под углом α = 45-φ/2 (рис. 2.6, а).
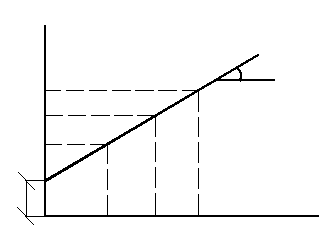
Для рыхлых песков и слабых глинистых грунтов разрушение проявляется в более интенсивном деформировании; образец приобретает бочкообразную форму (рис. 2.6, б). Первоначально зависимость (2.14) в механике грунтов была установлена более простыми испытаниями на плоскостных срезных (сдвижных) приборах. Образец грунта помещается в обойму, состоящую из двух половин, и через штамп загружается давлением σ. Затем к верхней половине обоймы прикладывается горизонтальная нагрузка Т и увеличивается, пока не произойдет срез (сдвиг) образца по плоскости разреза обойм. Предполагается, что при сдвиге реализуются максимальные для приложенного давления касательные напряжения Серия испытаний одинаковых образцов при разных давлениях позволяет непосредственно построить предельную прямую с уравнением (2.14), что и показано на рис. 2.7 для трех опытов (глина) и одного (песок). Для песчаного грунта, когда сцепление мало и им можно пренебречь, достаточно даже одного опыта (рис. 2.7, б). Практически проводят серию испытаний для возможности статистической обработки в связи с неоднородностью грунтов и разбросом результатов опытов. Недостатком испытаний на плоскостной сдвиг является некоторая неопределенность создаваемого в зоне сдвига НДС и принудительный характер плоскости сдвига: она предопределена конструкцией прибора, тогда как в стабилометре положение площадки сдвига определяется характером грунта. Тем не менее, испытания на срез широко применяются на практике. Очевидно, максимальное (предельное) касательное напряжение при сдвиге представляет собой сопротивление грунта сдвигу. Поэтому формула (2.14) выражает закон Кулона: сопротивление грунта сдвигу пропорционально давлению (нормальному напряжению σ) на площадке сдвига. В то же время (2.14, 2.16 и 2.17) можно назвать условием прочности Кулона – Мора, или условием предельного равновесия грунта в точке.
Надежное определение прочностных характеристик имеет большое значение, т.к. они используются во всех расчетах, связанных с прочностью и устойчивостью оснований и массивов грунта. Важно иметь ввиду, что показатели φ, с, сопротивление грунта сдвигу в целом зависят от состояния грунта, в особенности от плотности и влажности. Для водонасыщенных пылевато-глинистых грунтов, а также мелких и пылеватых песков важное значение имеет методика испытаний в условиях консолидации, т.е. уплотнения под нагрузкой и дренирования – отжатия воды из грунта. Пусть для одного и того же грунта – пластичной глины испытания на сдвиг проводятся по двум различным методикам: – консолидировано–дренированный (медленный) сдвиг, когда уплотняющее давление σ выдерживается до полного прекращения деформаций, и так же медленно прикладывается сдвигающая нагрузка (происходит отжатие поровой воды); – неконсолидировано–недренированный (быстрый) сдвиг, когда исключено отжатие воды и горизонтальная нагрузка быстро увеличивается до разрушения сразу после приложения уплотняющего давления. Результаты опытов будут совершенно различными (рис. 2.8).
Причина рассмотренного явления состоит в том, что под нагрузкой в малопроницаемом водонасыщенном грунте создается две системы давления:
где U – давление в поровой воде (поровое); σs – давление в скелете (эффективное). Собственно работу уплотнения грунта, реализующую силы трения, проводит только эффективное давление. Поэтому для рассматриваемых условий формулу (2.14) следует записать в виде:
Если испытание проводится по второй методике (прямая 2 на рис. 2.8), то возникшее поровое давление не успевает рассеяться, значение Естественно возникает проблема выбора методики испытаний при проектировании реальных сооружений. Некоторые рекомендации по этому вопросу имеются в стандартах на испытания. Общая же рекомендация состоит в том, что назначаемая методика должна соответствовать условиям работы грунта в основании проектируемого сооружения.
Таблица 3.1
Аналогичный прием можно применить для нагрузки, произвольно распределенной на площадке сложной формы. Площадка разбивается на ряд участков и на каждом распределенная нагрузка заменяется сосредоточенной силой. Далее используется (3.2). На прямоугольной площадке
Пусть нагрузка р распределена на площадке с размерами b, l (рис. 3.2). Тогда напряжения в любой точке основания можно определить аналогично формуле (3.2), приняв элементарную вертикальную нагрузку в виде dF = p·dx·dy и заменив суммирование интегрированием по площади. В итоге напряжение определяется по простой формуле:
где α – коэффициент рассеяния напряжений с глубиной, зависящий от положения рассматриваемой точки и формы загруженной площадки. Например, для точки на вертикали под центром площадки α есть функция двух безразмерных параметров
Напряжения по вертикали, проходящей через угловую точку, легко определить, используя эту же таблицу. Известно, что напряжение под углом в точке на глубине 2z равно одной четвертой осевого вертикального напряжения на глубине z. То есть, определив по табл. 3.2. значение α для Таблица 3.2
Напряжения в любых точках основания, не лежащих на центральной и угловых вертикалях, определяются по способу угловых точек. После определения напряжений в ряде точек напряженное состояние основания можно наглядно охарактеризовать изолиниями равных напряжений (изобарами, рис. 3.3). Все они проходят через угловые точки площадки, которые здесь (как и точка приложения сосредоточенной нагрузки на рис. 3.1) являются особыми точками.
Таблица 3.3
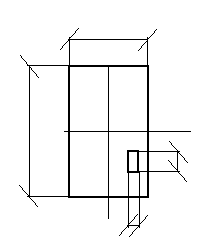
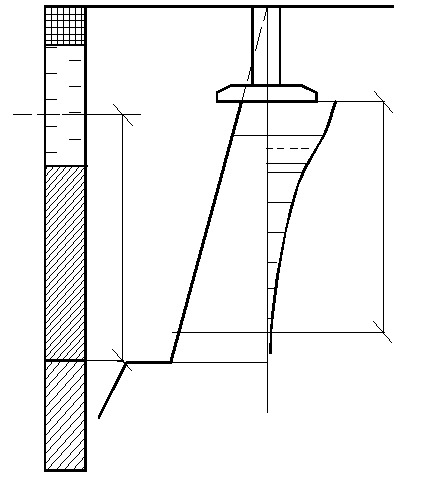
В виде, разрешенном относительно Е, формула (3.8) используется для полевого определения модуля деформации штампом. Значения коэффициента Пуасона ν в (3.8) при отсутствии экспериментальных данных допускается принять по виду грунта в пределах: – глины и суглинки nолутвердые и твердые ν = 0,1…0,15; – то же, тугопластичные - 0,2…0,25; – мягкопластичные и текучепластичные- 0,3…0,4; – текучие - 0,45…0,5; пески и супеси - 0,15…0,30. Реальные основания обычно слоистые, сжимаемость отдельных слоев различная и для расчета осадки чаще всего применяется метод послойного суммирования. Для большей наглядности рассматриваем применение метода в графоаналитической форме. Расчеты и сопровождающие их построения проводятся в следующем порядке: 1) Вычерчивается схема фундамента и геологического строения основания. 2) Строится эпюра природного давления σzg и ее ординаты в масштабе откладываются влево от z. В водоносном слое ниже WL учитывается взвешивание грунта в воде, а на кровле водоупора – скачок давления - γωнω. 3) Толща грунта под подошвой фундамента разбивается на расчетные слои h i =0,4b, где b – ширина подошвы фундамента. 4) По (3.9) определяется начальное уплотняющее давление Р0. 5) Определяется значение уплотняющего давления под центром (средней точкой) подошвы фундамента на границе каждого расчетного слоя: σzpi = αi· P0. (3.10) Значения Эпюра 6) Определяется нижняя граница сжимаемой толщи основания. Критерием ее установления в СНиП принято условие:
То есть в качестве нижней принимается граница того расчетного слоя, на которой уплотняющее давление в пять раз меньше природного. 7) В пределах сжимаемой толщи выделяются и нумеруются однородные расчетные слои грунта и определяется среднее уплотняющее давление в каждом слое. Например, на схеме (рис. 3.8) выделенный сначала второй расчетный слой большей частью попадает в песок, но захватывает и суглинок. Поэтому здесь нумеруются два слоя h2 , h3. Среднее давление равно полусумме значений на границах:
Для границы расчетных слоев 2,3 (рис. 3.8) значение уплотняющего давления можно взять непосредственно по эпюре, или найти по (3.10) для соответствующего значения α. 8) Определяется осадка каждого расчетного слоя в пределах сжимаемой толщи:
9) Определяется общая осадка суммированием осадок всех расчетных слоев:
Если под границей сжимаемой толщи, определенной по (3.11), находится слой сильносжимаемого грунта с модулем деформации Е < 5МПа, его осадка тоже должна быть учтена. В этом случае критерием определения НГСТ принимается: То есть осадку слабого слоя нужно учесть.
Приложения
Сопротивления основания
Рассмотрим ленточный фундамент с глубиной заложения d на однородном основании с характеристиками γ, φ, с. Считаем, что по подошве фундамента действует давление р = Fv/A, а с боков пригрузка γ·d за счет веса грунта в пределах глубины заложения. Используя формулу (3.4) и учитывая напряжения от веса грунта при ξ=1, получим следующие формулы для главных
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.32.115 (0.011 с.) |

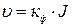 , (1.1)
, (1.1)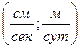 .
.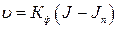 , где J n – начальный градиент.
, где J n – начальный градиент. , т/м3;
, т/м3;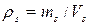 , т/м3;
, т/м3;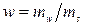 ,
,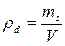 ;
;  ;
;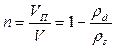 ,
,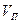 – объем пор в рассматриваемом объеме грунта V;
– объем пор в рассматриваемом объеме грунта V;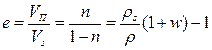 ; (1.2)
; (1.2)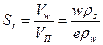 ,
, – плотность воды.
– плотность воды.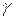 , частиц
, частиц  и сухого грунта
и сухого грунта 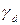 :
: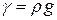 ;
; 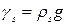 ;
; 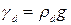 .
.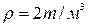 , то
, то 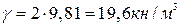 .
.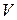 = 1 м3, то для него по смыслу пористости n – объем пор, а 1 – n = m – объем твердых частиц. Разрешая (1.2) относительно n, получаем:
= 1 м3, то для него по смыслу пористости n – объем пор, а 1 – n = m – объем твердых частиц. Разрешая (1.2) относительно n, получаем: 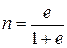 .
.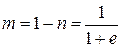 (1.3)
(1.3) . Принимая m по (1.3), получаем:
. Принимая m по (1.3), получаем:  .
.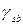 близко к 10 кН/м3.
близко к 10 кН/м3.
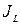 :
: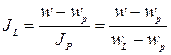 . (1.4)
. (1.4) <
< 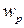
 < 0 и консистенция твердая; при
< 0 и консистенция твердая; при 
 очень существенно и для них в указанном интервале пластичной консистенции состояния детализируются:
очень существенно и для них в указанном интервале пластичной консистенции состояния детализируются: < 0,25 – полутвердое;
< 0,25 – полутвердое; 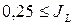 <0,5 – тугопластичное;
<0,5 – тугопластичное; 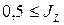 <0,75 – мягкопластичное;
<0,75 – мягкопластичное; 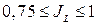 – текучепластичное.
– текучепластичное.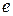 можно установить, если данный грунт подвергнуть максимально рыхлой укладке и максимально плотной, определив соответственно
можно установить, если данный грунт подвергнуть максимально рыхлой укладке и максимально плотной, определив соответственно  и
и 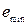 . Тогда, зная
. Тогда, зная 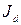
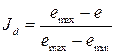 . (1.5)
. (1.5) – песок рыхлый; при 0,67<
– песок рыхлый; при 0,67< 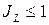 – плотный и при 0,33<
– плотный и при 0,33< 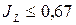 – средней плотности.
– средней плотности. . В зависимости от
. В зависимости от 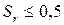 ), средней степени водонасыщения 0,5<
), средней степени водонасыщения 0,5< 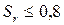 и насыщенные водой
и насыщенные водой 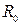 , интегрально характеризующее строительные свойства грунта как основания.
, интегрально характеризующее строительные свойства грунта как основания.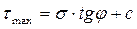 , (2.14)
, (2.14)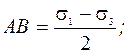 О 1В = О1О+ОК+КВ = с·сtgφ + σ3 +
О 1В = О1О+ОК+КВ = с·сtgφ + σ3 + 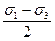 .
.

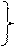
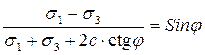 . (2.16)
. (2.16)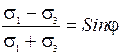 . (2.17)
. (2.17)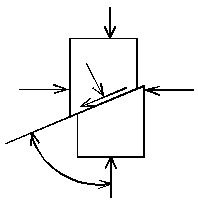
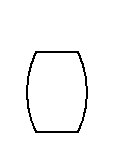
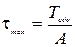 .
.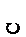


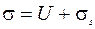 , (2.18)
, (2.18)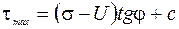 . (2.19)
. (2.19)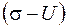 в (2.19) близко к нулю, трение почти не проявляется, что и дает слабо наклонную или даже горизонтальную прямую.
в (2.19) близко к нулю, трение почти не проявляется, что и дает слабо наклонную или даже горизонтальную прямую.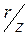
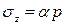 , (3.3)
, (3.3) и
и 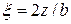 (табл. 3.2). С использованием табл. 3.2, задаваясь глубиной z, легко построить эпюру σz.
(табл. 3.2). С использованием табл. 3.2, задаваясь глубиной z, легко построить эпюру σz.
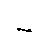




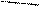
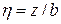 , напряжение в точке под углом на глубине 2z получим по формуле:
, напряжение в точке под углом на глубине 2z получим по формуле: 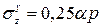 .
.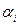 →f
→f 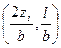 определяются для принятых zi по табл. 3.2;
определяются для принятых zi по табл. 3.2;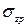 строится справа от оси z в том же масштабе, что и эпюра природного давления
строится справа от оси z в том же масштабе, что и эпюра природного давления 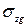 (рис. 3.8).
(рис. 3.8). . (3.11)
. (3.11) . (3.12)
. (3.12)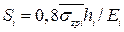 . (3.13)
. (3.13)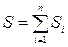 , где n – число однородных слоев (на схеме рис. 3.8 n=9).
, где n – число однородных слоев (на схеме рис. 3.8 n=9).


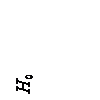

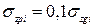 .
.


