
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Давление грунтов на подпорные стенкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Подпорная стенка удерживает массив грунта от обрушения. Различают гравитационные и шпунтовые подпорные стенки (рис. 4.7).
Основной нагрузкой для них является боковое давление грунта. Как подпорные стенки работают также стены подвалов зданий и подземных сооружений. В зависимости от величины и направления возможного смещения стенки на нее может действовать давление покоя, активное (распор) или пассивное давление (отпор). Активное давление возникает даже при небольших смещениях стенки от грунта засыпки; пассивное – при значительных смещениях стенки на засыпку. В обоих случаях грунт приходит в предельное состояние с формированием призмы обрушения (при активном) и призмы выпора при пассивном давлении. График изменения давления в зависимости от перемещения стенки показан на рис. 4.8.
Здесь нужно рассмотреть только давление для состояний предельного равновесия грунта. В состоянии покоя, когда нет боковых смещений, значение коэффициента бокового давления определяется формулой (2.3). Ограничиваемся рассмотрением гладкой вертикальной стенки с горизонтальной засыпкой (рис. 4.9). Пусть стенка имеет высоту h, засыпка представлена песком (φ≠0; с=0). Рассмотрим напряжения в точке задней грани стенки на глубине z. Поскольку стенка гладкая, вертикальное и горизонтальное напряжения в точке – главные, причем большее главное напряжение σz = σ1 = γz, а меньшее горизонтальное является активным давлением и равно: σа=σх=σ3=λаσ1=λаγ z, где
Эпюра изменения σ по высоте приведена на рис. 4.9 а. Равнодействующая активного давления равна площади треугольника и выражается формулой:
Пусть на поверхности засыпки действует равномерно распределенная нагрузка q. В этом случае эпюра активного давления трапецеидальная и равнодействующая или площадь эпюры (рис. 4.9, б) равна:
Рассмотрим учет сцепления грунта при определении активного давления. Ранее было установлено, что на высоту hкр по (4.11) связный грунт держит вертикальный откос. Считаем, что до этой глубины грунт не оказывает давления на стенку. Таким образом, эпюра начнется в точке на глубине hкр от верха стенки (рис. 4.9b). Нижняя ордината эпюры определится из УПР (2.16)
Равнодействующая давления равна:
Таким образом, учет сцепления уменьшает активное давление. В формулах (4.15 – 4.17) Еа измеряется в кН/м, т.е. давление устанавливается на единицу длины стенки. Пассивное давление возникает при смещении стенки на засыпку. При этом напряжение σz = σ3 минимальное, а σx = σ1 = σp максимальное, то есть является пассивным давлением. При этом из УПР (2.16) в точке 0≤ z ≤ h получаем
где
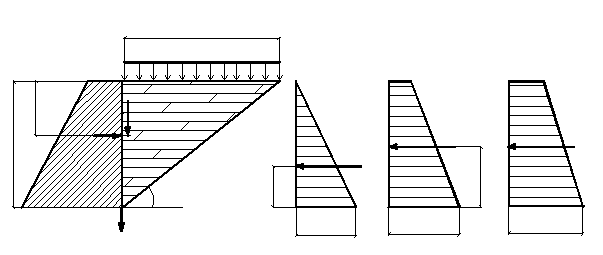
С помощью выражения (4.18) построены эпюры пассивного давления (рис. 4.10): а – при с=0, q=0; б – при с=0, q≠0; b – при q=0, с≠0. Для получения формул равнодействующих пассивного давления достаточно записать площади эпюр. Очевидно, для случаев а и б справедливы формулы (4.15) и (4.16) с заменой λа на λр по (4.19). Для грунта со сцеплением эпюра пассивного давления трапецеидальная, т.е. здесь учет сцепления увеличивает давление:
Следует также отметить различие в размерах призм обрушения и выпора (рис. 4.10 и 4.11):
В обоих случаях угол между направлением большего напряжения σ1 и плоскостью скольжения (обрушения или выпора) равен π/4 – φ/2, как это было указано для стабилометрических испытаний.
4. Задания на контрольную работу, примеры Решения задач
Контрольная работа включает шесть задач. Исходные данные по каждой задаче принимаются в соответствии с шифром, включающим две цифры и вариант (четный, нечетный). Шифр указывается преподавателем при выдаче задания на контрольную работу.
Работа оформляется в соответствии с общими правилами представляемых учебных работ на стандартной бумаге формата А4 в сброшюрованном виде. Обязательно приводится формулировка задачи со всеми исходными данными, затем ее полное решение. Пояснения должны быть краткими и ясными, схемы – четкими. Эпюры напряжений даются в масштабе. При вычислениях вначале приводится формула, затем ее запись в числах и результат с указанием единицы измерения. Задачи сопровождаются указаниями по их выполнению, а более сложные примерами решения.
Задача № 1. Перечислите классификации, используемые для песчаных и пылевато-глинистых грунтов. Рассчитайте производные физические характеристики, установите наименование грунта и определите его условное расчетное сопротивление. Определите вес минеральной части и воды в 1 м3 данного грунта. Укажите значение влажности для состояния полного водонасыщения грунта (полную влагоемкость). Исходные данные – по табл.1 и 2 соответственно для песчаных и глинистых грунтов. Пример выполнения. Пусть задан грунт – мелкий песок с характеристиками: γS = 26,4кH/м3; γ = 19,4кН/м3; ω = 0,25. По известным формулам определяем коэффициент пористости и степень влажности (учитывая, что γ = ρ · g и ρω = 1):
С использованием классификаций по плотности и степени влажности (см. п. 3.1.3 конспекта) устанавливаем полное название: песок мелкий, средней плотности, насыщенный водой. Таблица 1
Таблица 2
По справочным данным (табл. 1.2 конспекта) условное расчетное сопротивление песка как основания здания R0=200кПа. По смыслу физических характеристик имеем два уравнения (см. п. 3.1.3 конспекта): где
Решая систему, получаем Полную влагоемкость находим, приравнивая Sr (см. формулу в п.3.1.3. конспекта) единице и определяя влажность: Аналогично решается задача для глинистого грунта, когда исходные данные берутся из табл. 2.
Задача № 2. Построить эпюру вертикальных сжимающих напряжений. а). От вертикальной сосредоточенной нагрузки Fv – по вертикали, отстоящей от линии действия силы на расстоянии r (табл. 3); б). От нагрузки р, равномерно распределенной на прямоугольной площадке с размерами b x l – под центром площадки(табл. 4).
Таблица 3
Таблица 4
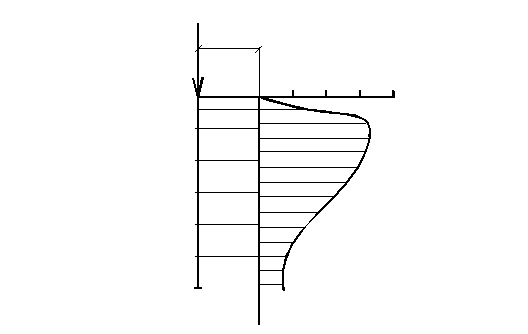
Указание. При построении эпюр использовать формулы (3.1) и (3.3) и данные табл. 3.1, 3.2 конспекта лекций. Пример выполнения. Построить эпюру сжимающих напряжений σz от вертикальной силы Fv=1000кН по вертикали, отстоящей от силы на расстоянии r=1,1м. Напряжение σz в произвольной точке основания определяется по формуле: σz =кFv/z2, где к – коэффициент влияния (табл. 3.1). Задаваясь рядом значений глубины z, для каждого r/z находим табличное к (табл. 5), вычисляем напряжения. При построении эпюры σz следует учитывать, что во всех точках поверхности, кроме точки приложения силы, напряжения отсутствуют (σ z = 0). Эпюра напряжений приведена на рис. 1. Таблица 5
Рис. 1
Указание. Для определения главных напряжений использовать формулу (3.4) конспекта. Эллипсы и эпюру напряжений построить в масштабе. Эпюру σz построить на оси OZ справа, задавшись рядом значений z.
Рис. 2
Таблица 6
Задача № 4. Фундамент с прямоугольной подошвой размерами b x ℓ и глубиной заложения d передает на основание вертикальную нагрузку FvII. Основание представлено мощным слоем грунта с характеристиками γII, Е, ν. Определить стабилизированную осадку по формуле Шлейхера и методом послойного суммирования. Объяснить причины расхождения результатов. Исходные данные – по табл. 7. Указание. Использовать пояснения и порядок расчета осадки, при веденные в п. 3.3.5 конспекта.
Таблица 7
Задача 5. Определить коэффициент устойчивости откоса, сложенного однородным грунтом с характеристиками γ, φ, с при заданном положении кривой скольжения в виде дуги окружности с центром в т. О 1 (рис. 3). Крутизна откоса 1: m, где Пример решения. Откос сложен однородным грунтом с характеристиками: γ=18 кН/м3, φ=300, С=10кПа. Высота откоса Н=5,0 м, крутизна 1:m, где m=1,5; На поверхности откоса приложена равномерно распределенная нагрузка q=20кПа. Определить коэффициент устойчивости откоса для h=10м.
Примем координатную систему XOZ; радиусом R=(h+H), проводим дугу окружности, выделив массив грунта DАВ (рис. 4). Координаты точек: О1 (0;–10); D (0; 5); А (mH,0) или А (7,5; 0). Из ∆ОО1 В имеем Тогда 1. Разделяем массив DАВ на 5 отсеков, нумеруя снизу вверх: 2. Записываем уравнение окружности с центром в т. О1 (0; –10): x 2 + (z +10)2 = R 2 или x 2 + z 2+20 z –125 = 0. Таблица 8
3. Используя последнее уравнение, вычисляем правые высоты отсеков. Например, для отсека №1: h 1 = z 1 – H / m. Значение z1 находим по уравнению (1) при х 1 = 2,5: z 1 = 4, 79м; тогда h 1 = 4,79–5ּ2/3 = 1,46м.
Аналогично: при х 2 = 5,0 z 2 = 4, 14м; и h 2 = 2,48м; при х 3 = 7,5 z 3 = h 3 = 2,99м; при х 4 = 9,5 z 4= h 4 =1,61м; при х 5 = 11,18 z 5= h5 =0. 4. Определяем площади отсеков; отсеки № 1, 5 считаем треугольниками, № 2, 3, 4 – трапециями:
5. Определяем вес отсеков единичной длины (ℓ = 1м); для отсеков 4, 5 учитываем действие нагрузки q = 20 кПа.
Силы Qi считаем приложенными в точках поверхности скольжения под центрами тяжести отсеков, т.е. в точках с абсциссами: x01=1,67 м; x02=3,75 м; x03=6,25 м; x04=8,5 м; x05=10,1 м.
6. Определяем центральные углы αi между вертикалью и радиусом в точку приложения веса отсека: Получаем: 7. Центральный угол, соответствующий дуге DB, равен Длина дуги кривой скольжения определяется из соотношения:
Составляем сводную таблицу для расчета коэффициента устойчивости:
Рассчитываем коэффициент устойчивости для принятого очертания поверхности скольжения:
Таким образом, для заданного положения поверхности скольжения откос устойчив: Таблица 9
В практических расчетах это условие должно выполняться для минимального коэффициента устойчивости, рассчитанного для наиболее опасной возможной поверхности скольжения.
Задача № 6. Охарактеризовать виды давления грунта на подпорную стенку и условия их возникновения. Построить эпюры активного и пассивного давления грунта на стенку с гладкими вертикальными гранями и горизонтальной поверхностью засыпки. Определить равнодействующие давлений, точки их приложения. Указать ширину призм обрушения и выпора. Обозначения по схеме на рис. 5, исходные данные принять по табл. 10.
Таблица 10
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1457; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.0.34 (0.015 с.) |





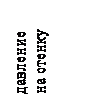

 – коэффициент активного бокового давления. Значение коэффициента λа следует из УПР (2.17):
– коэффициент активного бокового давления. Значение коэффициента λа следует из УПР (2.17): . (4.14)
. (4.14)




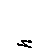

 . (4.15)
. (4.15) . (4.16)
. (4.16) .
. . (4.17)
. (4.17)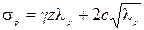 , (4.18)
, (4.18) - коэффициент пассивного бокового давления, равный:
- коэффициент пассивного бокового давления, равный: . (4.19)
. (4.19)


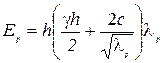 . (4.20)
. (4.20) (4.21)
(4.21) ;
;  .
. ;
; 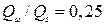 ,
,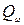 – вес воды в 1м3 грунта;
– вес воды в 1м3 грунта; – то же, вес скелета.
– то же, вес скелета. ;
;  .
. .
.


 ; откос нагружен равномерно распределенной нагрузкой q. Исходные данные – по табл. 8.
; откос нагружен равномерно распределенной нагрузкой q. Исходные данные – по табл. 8.


 ;
; 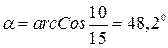 .
. . То есть т.В (11,18; 0)
. То есть т.В (11,18; 0)




 ;
; 
 ;
;  .
.


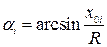 .
.

 .
.
 .
. .
. > 1.
> 1.







