
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Компрессионное сжатие грунта. Закономерность уплотнения. Формула Терцаги-ГерсевановаСодержание книги
Поиск на нашем сайте
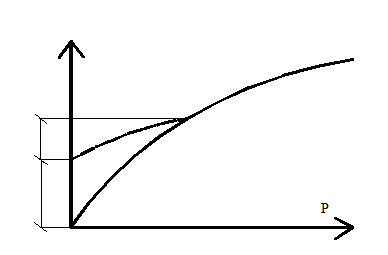
Из указанных ранее испытаний трехосное сжатие достаточно сложно, а одноосное применимо лишь к некоторым грунтам. Поэтому в механике грунтов широко применяется сжатие грунта вертикальным давлением в жесткой обойме, исключающей боковое расширение. Соответствующий прибор называется одометр. При испытании увеличивают вертикальное давление Результаты испытания можно представить зависимостью ε1=f(p) (рис. 2.2), представляющей собою плавную постепенно уполаживающуюся с ростом давления по мере уплотнения грунта кривую. Если при некотором давлении произвести разгрузку грунта, зависимость ε=f(p) будет отличаться от нагрузочной кривой. Таким образом общая деформация при давлении Р будет состоять из большей по величине остаточной или пластической и меньшей упругой или восстанавливающейся составляющих, т.е.
Если произвести повторные нагружения, грунт будет испытывать преимущественно упругие деформации. Такая работа характерна для грунта земляного полотна дорог. Рассмотрим возможность определения деформативных характеристик по результатам компрессии на основе (2.1). С учетом НДС и обозначений (
В обычных компрессионных испытаниях боковой распор q не определяется, поэтому последние два уравнения включают три неизвестных: q, E и v. Поэтому определить модуль деформации при некотором р можно, только если задаться значением коэффициента Пуассона. Тогда из второго уравнения можно найти отношение, называемое коэффициентом бокового давления: Подставим в первое уравнение (2.2), записав его в виде:
Разрешив полученное выражение относительно Е, получаем:
где β – коэффициент стеснения боковых деформаций при компрессии.
На практике результаты компрессии чаще представляют зависимостью коэффициента пористости от давления e = f(p), которую и называют компрессионной кривой (рис. 2.3). Коэффициент пористости при любой деформации где ен – начальное значение коэффициента пористости при р = 0.
В большом интервале изменения давления зависимости ei = f(p) нелинейны и очень разнообразны. На практике особенно важен участок кривой в некотором интервале давлений (рн, рк), где рн – начальное, природное давление в грунте; рк – конечное давление, возникающее после строительства сооружения. Для большинства сооружений этот интервал 0,3…0,4МПа. В указанном интервале кривую с небольшой погрешностью можно заменить секущей, т.е. принять: где m0 = tgφ – коэффициент сжимаемости. Соотношение (2.8) можно записать в более наглядной форме, если принять рн= 0и рк=р. Тогда
Установленную применимость соотношений (2.8; 2.9) можно характеризовать как закономерность уплотнения: «в ограниченном интервале давлений изменение коэффициента пористости прямо пропорционально давлению». Очевидно, это выражение принципа линейной деформируемости для условий компрессионного сжатия, а m 0 – деформативная характеристика грунта для этих условий. Размерность m 0 обратна размерности давления. Совместное рассмотрение формул (2.7) и (2.9) позволяет получить выражение для осадки слоя грунта в натурных условиях – например, при сплошной равномерно-распределенной на большой площади нагрузке (рис.2.4).
Формулу (2.7) для последней ступени нагрузки (i = к) можно записать в виде:
В расчетах часто используют относительный коэффициент сжимаемости Тогда из (2.10) следует простое выражение для осадки слоя грунта в условиях компрессионного сжатия (формула Терцаги-Герсеванова): S = m0 · p · h. (2.12) Поскольку характеристики компрессионного сжатия m0, mv и общие деформативные характеристики Е, v введены на основе общего принципа линейной деформируемости, между ними должна существовать связь. Действительно, сравнивая (2.10) и разрешенное относительно ε1 соотношение (2.5), получаем:
При v ≤ 0,3 значения β близки к единице, и тогда можно считать E и mν взаимно обратными величинами. Современные приборы компрессионного сжатия снабжены датчиками для определения бокового распора q. В этом случае из (2.3) непосредственно определяется коэффициент Пуассона.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 992; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.249.191 (0.006 с.) |

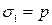 , радиальные напряжения возникают как реакции жестких стенок обоймы
, радиальные напряжения возникают как реакции жестких стенок обоймы 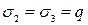 . Боковые деформации
. Боковые деформации 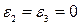 , а вертикальные ε2 = Δh/h определяются с помощью индикаторов. Таким образом, напряженное состояние образца пространственное (трехосное), а деформированное – одноосное.
, а вертикальные ε2 = Δh/h определяются с помощью индикаторов. Таким образом, напряженное состояние образца пространственное (трехосное), а деформированное – одноосное.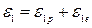 , причем
, причем 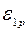 >
> 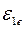 .
.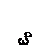



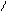

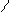

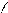
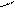
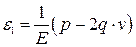 ;
; . (2.2)
. (2.2) . (2.3)
. (2.3)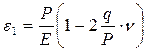 . (2.4)
. (2.4)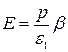 , (2.5)
, (2.5)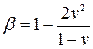 . (2.6)
. (2.6)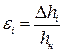 рассчитывается по формуле:
рассчитывается по формуле:  , (2.7)
, (2.7)
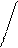
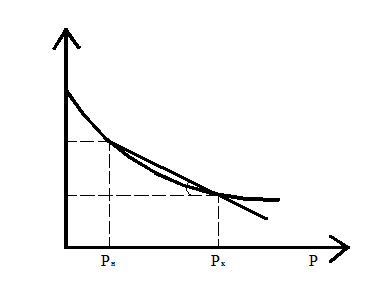
 , (2.8)
, (2.8)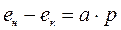 . (2.9)
. (2.9)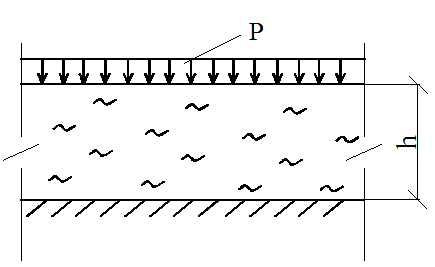
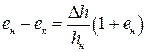 . Сравнивая с (2.9), имеем для деформации
. Сравнивая с (2.9), имеем для деформации . (2.10)
. (2.10)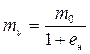 . (2.11)
. (2.11) . (2.13)
. (2.13)


