
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория предельного напряженного состояния грунтов и ееСодержание книги
Поиск на нашем сайте
Приложения
Определение начального критического давления и расчетного Сопротивления основания
Рассмотрим ленточный фундамент с глубиной заложения d на однородном основании с характеристиками γ, φ, с. Считаем, что по подошве фундамента действует давление р = Fv/A, а с боков пригрузка γ·d за счет веса грунта в пределах глубины заложения. Используя формулу (3.4) и учитывая напряжения от веса грунта при ξ=1, получим следующие формулы для главных напряжений в т. М. (рис. 4.1)
Подставив (4.1) в УПР (2.16), получаем выражение, связывающее нагрузку р с координатами рассматриваемой т. М β, z, глубиной заложения d, характеристиками грунта γ, φ, с, т.е.
Если в т. М выполняется УПР, то площадки сдвига совпадут с лучами из точки к краям подошвы и тогда Р1кр = Мq ·γ·d +Mc ·C, (4.3) где Мq и Mc – функции угла внутреннего трения, определяемые соотношениями:
Применение формулы (4.3) приводит к надежным, но не экономичным решениям; практикой доказано, что без ущерба для надежности можно допустить работу основания в начале стадии сдвигов (см. рис. 2.1), когда зависимость s = f(р) еще близка к линейной. Наибольшее применение получила формула, получаемая на основе (4.2), в которой принимается z = 0,25b. При этом (4.3) обобщается на учет ширины подошвы: Рнач. =Мγ ·γ ·d+Mq ·γ ·d+Mc ·C, (4.5) где В нормах проектирования Рнач. называется расчетным сопротивлением основания Рнач.= R. Формула (4.5) обобщена с учетом следующих факторов: – вид грунта и достоверность определения его характеристик; – жесткость сооружения; – возможность разной глубины заложения c двух сторон фундамента; – разброс значений характеристик.
Основы теории предельного напряженного состояния (ТПНС) и определение второй критической (предельной) нагрузки
При значительном развитии областей сдвигов, когда грунт близок к разрушению, использование уравнений ТЛДС (4.1) уже невозможно. Здесь необходимо использовать более общие соотношения – дифференциальные уравнения равновесия грунта в точке. Для условий плоской задачи, используя схему и обозначения на рис. 4.2 и приравнивая нулю суммы проекций на координатные оси, получаем:
К уравнениям (4.6) присоединяется условие предельного равновесия (2.16), которое следует записать, как и (4.6), через компоненты σx, σz, τ:
Уравнения (4.6) и (4.7) составляют систему уравнений ТПНС для условий плоской задачи. Отыскание напряжений, удовлетворяющих уравнениям (4.6, 4.7), позволяет находить предельную нагрузку на основание, устанавливать устойчивость откосов, определять давление грунта на подпорные стены и т.п. Весь этот круг задач составляет область приложения ТПНС. Задачи ТПНС решаются различными методами: аналитически, с помощью приближенных инженерных приемов и численными методами с преобразованием системы (4.6, 4.7) и заменой производных конечными разностями. Соответствующие решения получены Соколовским В.В., Березанцевым В.Г. и др. Формулы для определения второго критического давления приводятся обычно к трехчленной форме, как и (4.5). На основе анализа и обобщения решений ТПНС с учетом опытных данных в нормах проектирования принята следующая формула для предельного давления на основание внецентренно нагруженного фундамента произвольной формы:
где Nγ, Nq, Nc – коэффициенты несущей способности, определяемые по табл. 4.1 в зависимости от расчетного значения φI и угла наклона равнодействующей нагрузки к вертикали δ; γI и γ΄I – расчетные значения удельного веса грунта под подошвой в пределах глубины заложения фундамента d; ξγ, ξq, ξc – коэффициенты формы подошвы фундамента (для ленточного фундамента ξγ=ξq=ξc=1); b΄ – приведенная ширина подошвы фундамента. Таблица 4.1
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 983; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.17.3 (0.007 с.) |

 . (4.1)
. (4.1) (4.2)
(4.2)





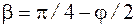 , так что по (4.2) р будет зависеть только от z – максимальной глубины развития областей сдвига. Первое критическое давление получим, если примем z = 0 (области сдвига полностью отсутствуют). Это решение впервые было получено профессором Пузыревским Н.П. Формулу можно представить в виде:
, так что по (4.2) р будет зависеть только от z – максимальной глубины развития областей сдвига. Первое критическое давление получим, если примем z = 0 (области сдвига полностью отсутствуют). Это решение впервые было получено профессором Пузыревским Н.П. Формулу можно представить в виде: (4.4)
(4.4)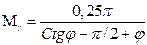 , а коэффициенты Mq, Mc по (4.4).
, а коэффициенты Mq, Mc по (4.4). (4.6)
(4.6) . (4.7)
. (4.7)


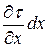

 , (4.8)
, (4.8)


