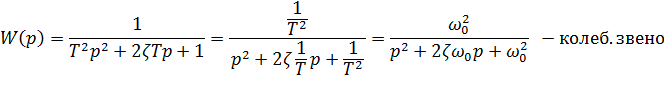Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виды систем автоматического управления (сау)Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
ВИДЫ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ (САУ) Автоматическое управление – это устройство, которое осуществляет управление без человека. САУ – совокупность объекта управления и технических средств автоматизации.
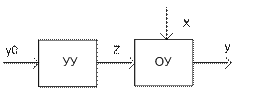
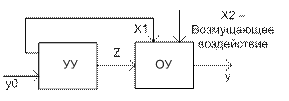
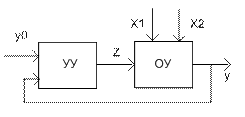
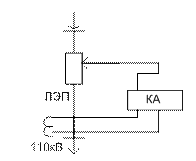
1. Разомкнутое управление: Устройство управления вырабатывает вырабатывающее воздействие Z, которое поступает на объект управления. На входе в устройство управления присутствует сигнал y0, который представляет собой задающее воздействие. 2. Управление по возмущению: Управляющее воздействие компенсирует влияние одного из возмущений на управляемую величину у, обычно компенсирует наиболее существенное возмущение X1 в результате изменения выходного параметра у под влиянием всей совокупности внешних воздействий Х уменьшится, но не может быть полностью устранено. 3. Замкнутое управление: Принцип замкнутого управления позволяет решить задачу управления при любом характере действующих возмущений. АВТОМАТИЧЕСКОЕ УПРАВЛЕНИЕ В ЭНЕРГЕТИКЕ Процесс выработки, передачи и распределения эл. энергии имеет ряд особенностей: - огромное количество вырабатываемой и передаваемой электроэнергии в течении длительного времени. - непрерывность процесса выработки, передачи и распределения - большие скорости протекания процессов. Когда технологическая цепь между вырабатываемой и потребляемой энергией нарушается, в месте повреждения выделяется большое количество энергии в виде тепла, что в свою очередь приводит к повреждениям в оборудовании и недоотпуску энергии. Устройства автоматизации энергосистем по своему назначению и выполняемым функциям разделяют на 2 вида: 1. устройства обеспечивающие надежность работы энергосистемы, бесперебойность электроснабжения при аварийных режимах. А) устройства релейной защиты
Б) устройства противоаварийной автоматики. 2. устройства автоматизации, которые обеспечивают должные качественные показатели электроэнергии, экономичность работы всей энергосистемы, контролируют U, f, P, Q. ФУНКЦИОНАЛЬНАЯ СХЕМА АВТОМАТИЧЕСКОГО РЕГУЛЯТОРА И ЕГО ОСНОВНЫЕ ОРГАНЫ Устройство управления совместно с элементами обратной связи называется автоматическим регулятором. ЭЛЕМЕНТЫ РЕГУЛЯТОРА:
Элементы регулятора выполняют следующие функции: 1 – измерение и преобразование регулируемой величины у. 2 – формулируют заданное значение у0 заданной величины. 3 – выявление отклонения регулируемой величины у от заданного значения. 4 – вырабатывается управляемое воздействие. Наиболее распространенным законом регулирования является
Основной недостаток П-регулятора заключается в невозможности поддержания величины на постоянном уровне при изменении внешних воздействий. Интегральный регулятор (И-регулятор): Дифференциальный регулятор: ПИД-регулятор: СТАТИЧЕСКОЕ И АСТАТИЧЕСКОЕ РЕГУЛИРОВАНИЕ
Если на объект управления действует возмущение Х, то имеет значение статическая характеристика у=f(x) при y0=const. Два вида характеристик:
Статическая характеристика всегда имеет наклон, система называется статической, если при постоянном внешнем воздействии ошибка В случае, когда статическая ошибка недопустима используют астатическое регулирование, основная особенность при постоянном входном воздействии ошибка регулирования стремится к нулю вне зависимости от величины воздействия. Обеспечение требуемой статической точности регулирования является основной задачей при расчёте САР.
ПЕРЕДАТОЧНАЯ ФУНКЦИЯ Передаточная функция – это наиболее общая универсальная форма зависимости между выходным и входным сигналом и представляет собой отношение операторных изображений выходного сигнала к входному сигналу при нулевых начальных условиях.
Зная передаточную функцию звена и операторное изображение входного сигнала можно определить операторное изображение выходного сигнала.
Если изображение входного сигнала неизвестно, то его находят по формуле прямого преобразования Лапласа.
p – оператор Лапласа. Для получения выходного сигнала функции времени применяют обратное преобразование Лапласа:
Оригинал: Изображение:
1(t)
Передаточная функция может быть получена из дифференциального уравнения звена, для чего необходимо выполнить следующую операцию: 1) 2) 3) ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ При подаче на вход линейного звена синусоидального сигнала на его выход устанавливается синусоидальный сигнал той же частоты, но с другой амплитудой фаз.
Зависимость частотного отношения амплитуд выходных и входных синусоидальных сигналов называется амплитудно-частотной характеристикой (АЧХ).
Зависимость от частоты разности фаз между выходным и входным сигналом называется фазовой частотной характеристикой (ФЧХ).
Зависимость от частоты отношения комплексов входного и выходного синусоидального сигнала называется амплитудно-фазовой частотной характеристикой (АФЧХ).
Логарифмическая (АФЧХ): ЛАЧХ:
ЛАЧХ – зависимость логарифма отношения амплитуд выходного сигнала от логарифма частоты.
[Белл] (используется дБ)
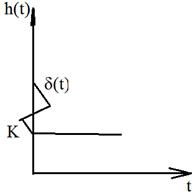
ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО
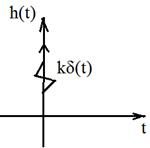
1. Переходная 2. АФЧХ
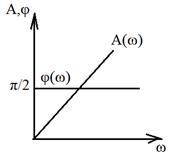
Совпадает с положительной мнимой осью. 3. АЧХ
Для всех частот диф. Звено вносит постоянный фазовый сдвиг на угол 4. ЛАЧХ
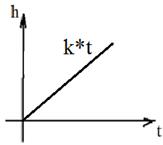
Звено технически не реализуется и используется как удобная математическая абстракция. ИНТЕГРИРУЮЩЕЕ ЗВЕНО Выполняет интегрирование входного сигнала.
1. Переходная
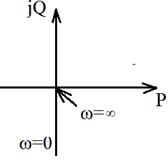
2. АФЧХ
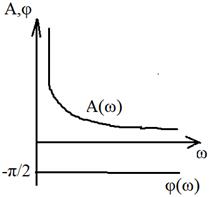
3. АЧХ 4. ФЧХ 5. ЛАЧХ
Колебательное звено
1. Переходный процесс: 2. АФЧХ:
1. 2.
Форсирующее звено
Также как и дифференцирующее, форсирующее звено в идеальном виде не реализуется. Факторы, которые препятствуют физической реализации: 1. выходной сигнал появляется раньше входного 2. нереализуемая частотная характеристика 3. появление на выходе бесконечных значений сигнала в конечные моменты времени.
ЛАЧХ:
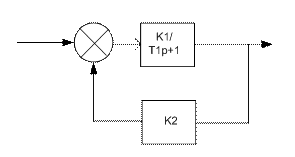
ЗВЕНО С ОБРАТНОЙ СВЯЗЬЮ Звено с обратной связью:
Одновременно с входным сигналом на вход подается выходной сигнал, прошедший через звено обратной связи. И если выходной сигнал суммируется с входным сигналом, то положительная обратная связь. А если от выходного вычитается входной сигнал, то отрицательная обратная связь.
Жёсткая обратная связь:
Гибкая обратная связь:
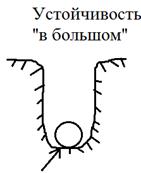
ПОНЯТИЕ УСТОЙЧИВОСТИ И ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ Устойчивость – это способность системы возвращаться в предшествующее установившееся состояние после внезапного изменения внешних воздействий. Различают устойчивость “в малом” (статическая устойчивость); “в большом” (динамическая устойчивость).
Поведение любой системы описывается линейно или линеаризовано к диф. уравнению, решение которого относительно одной из переменных может быть записано следующим образом:
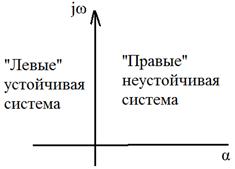
где p – корень характеристического уравнения. САР будет устойчива, если все корни характеристического уравнения будут вещественными отрицательными, либо комплексными, но с отрицательной вещественной частью.
Критерий устойчивости – это правила, которые позволяют судить о знаках корней характеристического уравнения без его решения. - Алгебраические критерии - Частотные критерии (которые используют частотные хар-ки). По виду характеристического уравнения можно сразу сформулировать необходимый признак устойчивости системы: Если все коэффициенты характеристического уравнения положительны, то это является необходимым условием устойчивости системы. Причем для системы 1 и 2-го порядка положительность коэффициентов является достаточным условием.
КРИТЕРИЙ РАУСА К достоинствам метода относятся простая реализация на ЭВМ, а также простота анализа для систем небольшого (до 3) порядка. К недостаткам можно отнести ненаглядность метода, по нему сложно судить о степени устойчивости, о её запасах.
Число строк в таблице Рауса равняется n+1. В первых двух строках записываются коэффициенты характеристического уравнения в соответствии с их индексами. Коэффициентам с отрицательными индексами соответствуют нули.
Формулировка критерия Рауса: Для устойчивости САР необходимо и достаточно, чтобы коэффициенты 1-го столбца были положительными. Если не все коэффициенты 1-го столбца положительны, то число корней уравнения лежащих в правой полуплоскости равно числу переменных знаков в первом столбце таблицы. Если Диагональные миноры критерия Гурвица могут определяться независимо друг от друга и в этом заключается основное достоинство. Для применения критерия Рауса необходимо постепенное заполнение таблицы, однако для систем высокого порядка объем вычислений оказывается гораздо меньше чем для критерия Гурвица.
КРИТЕРИЙ ГУРВИЦА Достоинством метода является простота, недостатком - необходимость выполнения операции вычисления определителя. Критерий Гурвица позволяет судить об отсутствии правых корней характеристического уравнения по знакам диагональных миноров в определителе Гурвица.
По главной диагонали располагаются коэффициенты характеристического уравнения начиная с an-1 по a0 в порядке убывания. Затем столбцы дополняются коэффициентами характеристического уравнения: вверх – в порядке убывания индексов; вниз – в порядке их увеличения. Члены столбцов с индексами больше чем n и меньше 0 принимаются равными нулю.
Необходимым и достаточным условием отсутствия правых корней является положительность всех корней и диагональных миноров.
Важным условием устойчивости является положительность последнего диагонального минора. КРИТЕРИЙ МИХАЙЛОВА В основу критерия Михайлова положен принцип аргумента, известный из теории функции комплексных элементов.
Вектор
Если pi расположено справа, то поворот будет по часовой стрелке с приращением
Если все корни лежат в левой полуплоскости, то
m корней правое; (n-m) левое.
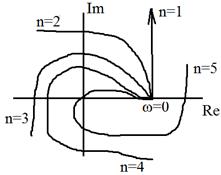
Т. о. правило аргумента формулируется следующим образом: приращение аргумента вектора На основании принципа аргумента Михайлов сформулировал критерий: для устойчивости САР необходимо и достаточно, чтобы годограф характеристического вектора
КРИТЕРИЙ НАЙКВИСТА Позволяет судить об устойчивости замкнутой системы по её АФЧХ:
-характеристическое уравнение разомкнутой САУ.
- характеристическое уравнение замкнутой САУ. Рассмотрим функцию:
-Отношение характеристического уравнения замкнутой системы к характеристическому уравнению разомкнутой системы.
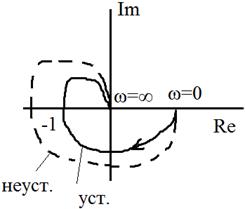
Определяется разностью приращений аргументов замкнутой и разомкнутой системы. Следовательно, имея АФЧХ разомкнутой системы и применяя правило аргумента по вот этому выражению можно определить устойчивость замкнутой системы. 1) Разомкнутая система устойчива. 2) Разомкнутая система неустойчива.
Для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ устойчивой либо нейтральной, находящейся на границе устойчивости разомкнутой САУ не охватывала точку с координатами (-1;j0). Для устойчивости замкнутой системы необходимо, чтобы АФЧХ неустойчивой разомкнутой системы охватывало 0,5m раз точку с координатами (-1;j0) в положительном направлении, где m – число правых корней.
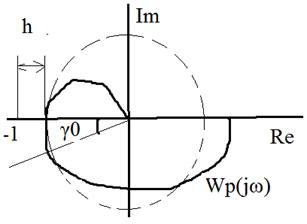
ЗАПАСЫ УСТОЙЧИВОСТИ Частотные запасы устойчивости определяют в соответствии с критерием Найквиста удалением АФЧХ разомкнутой системы от критической точки с координатой (-1;j0).
В условиях эксплуатации параметры системы по тем или иным причинам могут изменяться, что может привести к работе системы вблизи критической точки, либо вообще к потере устойчивости. Запас устойчивости h – характеризует удаление годографа от критической точки по отрицательно действительной оси. Обеспечивается крайней неустойчивостью при изменении коэффициента усиления. Второй запас – это запас устойчивости по фазе, определяется углом
ПОНЯТИЕ О КАЧЕСТВЕ САР Устойчивость системы является необходимым, но не достаточным условием функционирования. Показатели, которые наиболее полно характеризуют систему это: 1. точность поддержания регулируемой величины 2. быстродействие 3. характер изменения регулируемой величины в переходном режиме 4. запасы устойчивости по модулю и по фазе Задача анализа качества регулирования, выяснения, удовлетворяет ли система требованиям качества? Устанавливается, какое влияние протекание переменного процесса оказывают параметры системы. Качество регулирования в установившемся режиме может быть оценено по передаточной функции, либо по частотным характеристикам, а в переходном режиме используются прямые показатели качества, которые основаны на анализе передаточной характеристики, либо косвенно, не требующие получения переходной характеристики.
ОШИБКИ РЕГУЛИРОВАНИЯ Точность работы САР характеризуется степенью приближения регулируемой величины У к задающему воздействию У0.
Регулируемая величина изменяется под влиянием 2 возмущений = внешняя нагрузка (Х), задающее воздействие (У0). Операторное изображение ошибки имеет 2 составляющие:
Можно получить операторное выражение ошибки регулирования. Причем эта ошибка может быть представлена в виде двух составляющих: - установившаяся ошибка (точность поддержания регулируемой величины в установившемся режиме); - переходная ошибка (определяет качество регулирования в переходном режиме). Установившаяся ошибка регулирования:
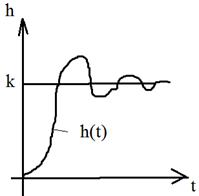
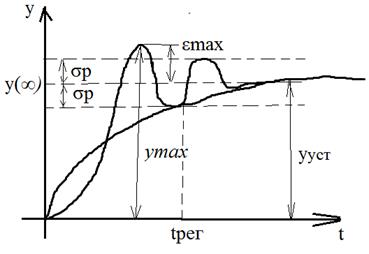
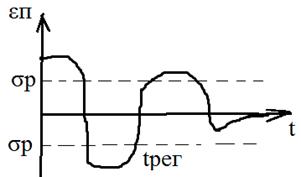
ПРЯМЫЕ ПОКАЗАТЕЛИ КАЧЕСТВА Переходная составляющая ошибки определяется при единичном ступенчатом воздействии:
Колебательный процесс наиболее характерен для большинства быстродействующих систем. При этом регулирующая величина может переходить через новое установившееся значение в сторону противоположную начальному значению величины (перерегулирование). Показатели качества: 1) Максимальное перерегулирование – отношение разности между максимальным и установившимся значением регулируемой величины к её установившемуся значению в процентах.
В системах поддерживающих регулируемую величину при изменении внешних воздействий 2) Время регулирования – промежуток t от момента возникновения возмущений до момента, когда абсолютное значение переходной погрешности становится меньше некоторого заданного значения. 3) Число колебаний регулируемой величины за время переходного процесса. Прямые показатели качества наиболее достоверно характеризуют динамические свойства системы. Недостатки: 1) Сложность получения переходной характеристики 2) Отсутствие явных аналитических зависимостей между показателями качества и показателями системы. Поэтому наряду с прямыми широко используются косвенные методы.
КОРНЕВЫЕ МЕТОДЫ Корневые методы позволяют оценивать характер переходного процесса по отношению корней характеристического уравнения.
Поскольку характер переходного процесса зависит не только от знаменателя передаточной функции, но и от его числителя, то использование корневого метода особенно эффективно для передаточных функций вида:
Область ограничиваемая 2 прямыми параллельна мнимой оси, проходящей на расстояние.
Также используются прямые, проходящие из начала координат под углом:
Абсолютное значение вещественного корня, наиболее близко расположенного к началу координат называется апериодической границей устойчивости. В случае комплексных корней содержащую вещественную часть наиболее близко расположенную к началу координат и называется колебательностью системы.
Чем больше Ближайшему к мнимой оси корню соответствует наиболее медленно затухающая составляющая переходной погрешности, поэтому величина
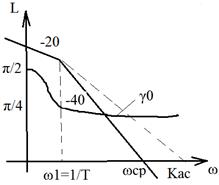
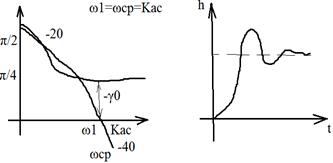
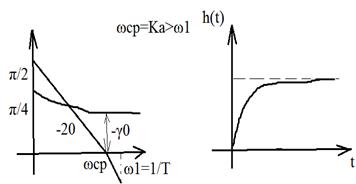
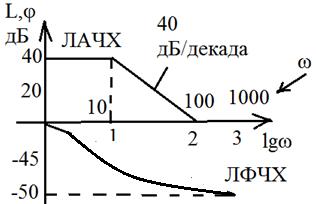
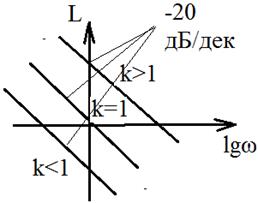
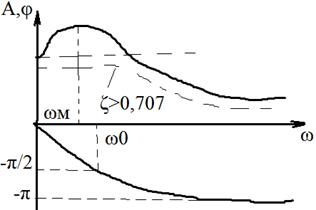
ОЦЕНКА КАЧЕСТВА ПО ЛАЧХ
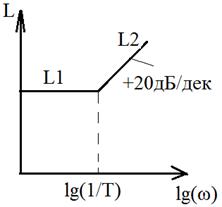
ЛАЧХ:
Приемлемое качество достигается в том случае, когда участок асимптотической ЛАЧХ с наклоном -20 дб/дек пересекает горизонтальную ось. Чем больше длина этого участка тем при прочих равных условиях будет больше запас по фазе.
ВИДЫ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ (САУ) Автоматическое управление – это устройство, которое осуществляет управление без человека. САУ – совокупность объекта управления и технических средств автоматизации.
1. Разомкнутое управление: Устройство управления вырабатывает вырабатывающее воздействие Z, которое поступает на объект управления. На входе в устройство управления присутствует сигнал y0, который представляет собой задающее воздействие. 2. Управление по возмущению: Управляющее воздействие компенсирует влияние одного из возмущений на управляемую величину у, обычно компенсирует наиболее существенное возмущение X1 в результате изменения выходного параметра у под влиянием всей совокупности внешних воздействий Х уменьшится, но не может быть полностью устранено. 3. Замкнутое управление: Принцип замкнутого управления позволяет решить задачу управления при любом характере действующих возмущений.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 4510; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.238.221 (0.017 с.) |



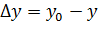

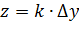
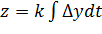

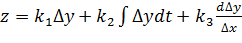
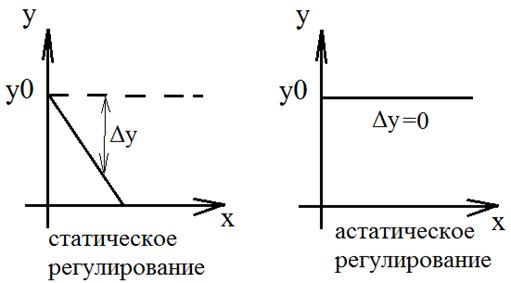
 стремится к постоянному значению зависящему от величины воздействия.
стремится к постоянному значению зависящему от величины воздействия.
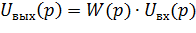

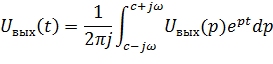
 1
1

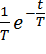
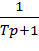
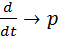
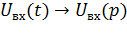
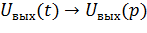
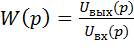
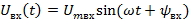

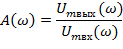
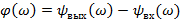
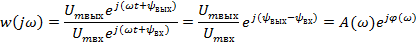
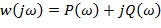
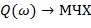


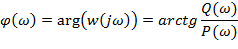

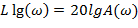
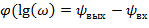
 W(p)=kp
W(p)=kp





 .
.
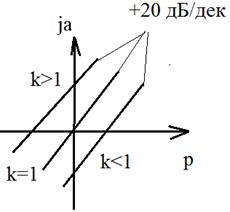





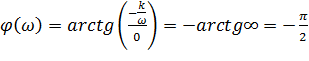

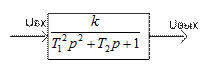
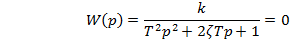
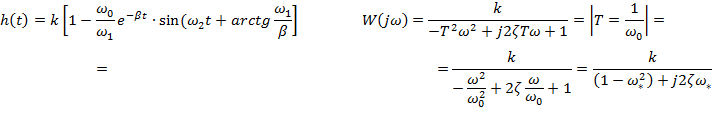

 ЛАЧХ
ЛАЧХ
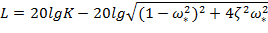
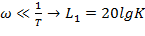
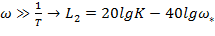


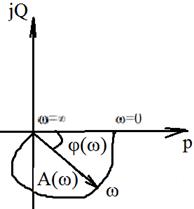
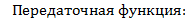 АФЧХ:
АФЧХ: 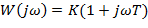
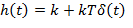

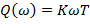
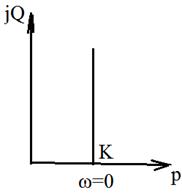

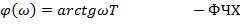

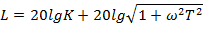
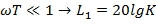 - прямая
- прямая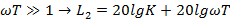

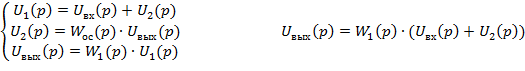
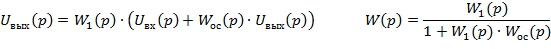
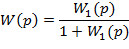
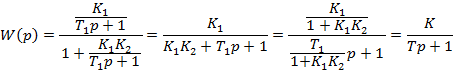

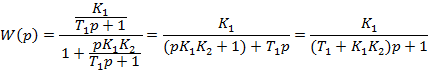

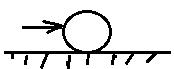 Объект нейтрален, т.к. после внешнего воздействия он приходит в новое равновесное состояние, которое существенно отличается от предыдущего.
Объект нейтрален, т.к. после внешнего воздействия он приходит в новое равновесное состояние, которое существенно отличается от предыдущего. Объект неустойчив.
Объект неустойчив.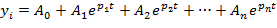
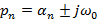
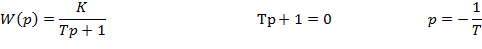

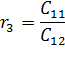


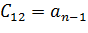

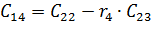

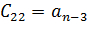
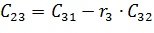
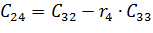

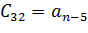
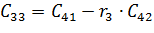 ……………….
……………….

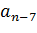 ……
……
……
……
 то это указывает на наличие пары чисто мнимых корней и это будет граница колебательной устойчивости. Если коэффициент a0=0, то в ноль обращается
то это указывает на наличие пары чисто мнимых корней и это будет граница колебательной устойчивости. Если коэффициент a0=0, то в ноль обращается 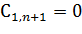 и это будет граница апериодической устойчивости.
и это будет граница апериодической устойчивости.






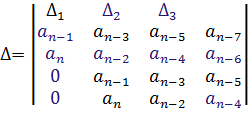





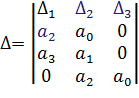
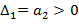
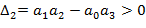
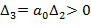
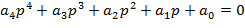






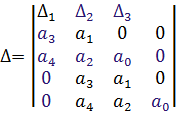

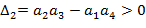
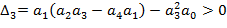
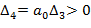
 Если a0=0, то система имен нулевой корень и находится на границе апериодичности устойчивости. Если
Если a0=0, то система имен нулевой корень и находится на границе апериодичности устойчивости. Если 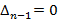 , то система имеет пару мнимых корней и находится на границе колебательной устойчивости.
, то система имеет пару мнимых корней и находится на границе колебательной устойчивости.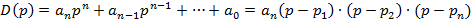

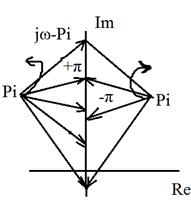
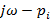 будет перемещаться с положительным направлением (против часовой стрелки) и получим приращение
будет перемещаться с положительным направлением (против часовой стрелки) и получим приращение 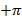 .
.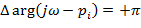
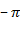 .
.

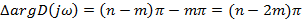
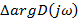 при изменении частоты от
при изменении частоты от  равно разности между чистом (n-m) левых корней и числом m правых корней, умноженных на
равно разности между чистом (n-m) левых корней и числом m правых корней, умноженных на 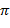 . Т. е. (n-2m)
. Т. е. (n-2m) 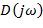 начинаясь при
начинаясь при 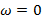 на действительной оси с ростом частоты от 0 до
на действительной оси с ростом частоты от 0 до  обходил последовательно в положительном направлении (против часовой стрелки)
обходил последовательно в положительном направлении (против часовой стрелки) 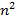 , где n – порядок хар. уравнения.
, где n – порядок хар. уравнения.
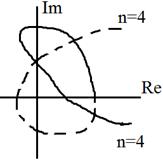 - Годограф для неустойчивой системы:
- Годограф для неустойчивой системы:


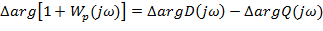



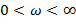
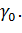 Запас устойчивости по фазе обеспечивает сохранение устойчивости системы при увеличении запаздывания.
Запас устойчивости по фазе обеспечивает сохранение устойчивости системы при увеличении запаздывания.
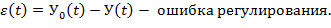
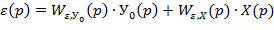


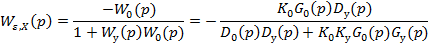
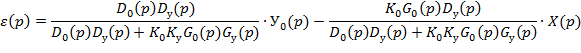
 Установившаяся ошибка при постоянном ступенчатом воздействии называется статической ошибкой и для её определителя используется предельная теорема:
Установившаяся ошибка при постоянном ступенчатом воздействии называется статической ошибкой и для её определителя используется предельная теорема: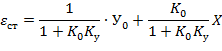
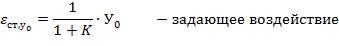
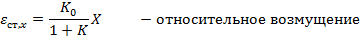
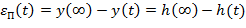
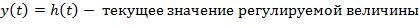
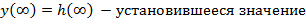
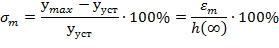
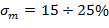
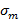 может быть больше.
может быть больше.
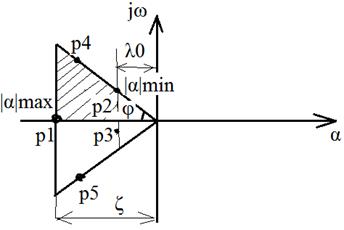

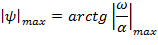

 тем больше максимальное перерегулирование в системе и больше количество колебаний. Чем выше
тем больше максимальное перерегулирование в системе и больше количество колебаний. Чем выше 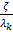 тем меньше влияние малых постоянных времени и тем больше возможность представить систему уравнением низкого порядка.
тем меньше влияние малых постоянных времени и тем больше возможность представить систему уравнением низкого порядка. позволяет определить время регулирования:
позволяет определить время регулирования:
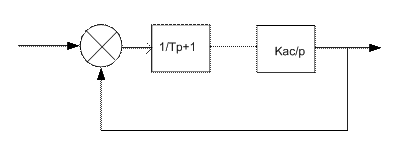
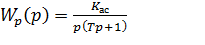 Kас – коэффициент астатизма.
Kас – коэффициент астатизма.