
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение устойчивости по логарифмическим характеристикамСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть известны частотные характеристики двух разомкнутых систем, которые отличаются друг от друга только коэффициентом передач. Пусть первая система будет устойчивая, а вторая – неустойчивая.
АФЧХ:
ЛАЧХ:
Сравнивая АФЧХ и логарифмические характеристики можно установить, что система в замкнутом состоянии будет устойчива, если значение фазовой характеристики
ОБЩАЯ ХАРАКТЕРИСТИКА МЕТОДА D-РАЗБИЕНИЯ
Такому перемещению точки пространства коэффициентов будет соответствовать перемещение корней характеристического уравнения на комплексной плоскости.
Совокупность коэффициентов, при которых хотя бы один корень находится на мнимой оси определяет поверхность в пространстве коэффициентов и эта поверхность делит пространство коэффициентов на области в зависимости от количества правых корней.
Особый интерес представляет область D(0), которой соответствует характеристическое уравнение с отсутствием правых корней. Такая область называется областью устойчивости. Обычно область устойчивости выделяет в пространстве каких-либо варьирующихся параметров.
D-РАЗБИЕНИЯ ПО ОДНОМУ ПАРАМЕТРУ Используется в том случае, когда исследуемое влияние на устойчивость только одного параметра. Часто им является коэффициент усиления.
Кривая построенная в координатах U и V на комплексной плоскости при различных значениях частоты и будет границей для разбиения.
D-РАЗБИЕНИЯ ПО ДВУМ ПАРАМЕТРАМ Пусть 2 параметра K1 и K2 входят в характеристическое уравнение линейно (ни в одном из коэффициентов хар. ур. нет произведения и нет высших степеней K).
Задавая изменение частоты от 0 до
УСТОЙЧИВОСТЬ СИСТЕМЫ СО ЗВЕНЬЯМИ ЗАПАЗДЫВАНИЯ
Условие устойчивости – это отсутствие правых корней характеристического уравнения.
Сначала строят годограф без запаздывания
При возрастании частоты угол поворота увеличивается, а величина вектора А уменьшается, поэтому графический годограф системы с запаздыванием “закручивается” относительно начала координат. Будем увеличивать запаздывание
ПОНЯТИЕ О КАЧЕСТВЕ САР Устойчивость системы является необходимым, но не достаточным условием функционирования. Показатели, которые наиболее полно характеризуют систему это: 1. точность поддержания регулируемой величины 2. быстродействие 3. характер изменения регулируемой величины в переходном режиме 4. запасы устойчивости по модулю и по фазе Задача анализа качества регулирования, выяснения, удовлетворяет ли система требованиям качества? Устанавливается, какое влияние протекание переменного процесса оказывают параметры системы. Качество регулирования в установившемся режиме может быть оценено по передаточной функции, либо по частотным характеристикам, а в переходном режиме используются прямые показатели качества, которые основаны на анализе передаточной характеристики, либо косвенно, не требующие получения переходной характеристики.
ОШИБКИ РЕГУЛИРОВАНИЯ Точность работы САР характеризуется степенью приближения регулируемой величины У к задающему воздействию У0.
Регулируемая величина изменяется под влиянием 2 возмущений = внешняя нагрузка (Х), задающее воздействие (У0). Операторное изображение ошибки имеет 2 составляющие:
Можно получить операторное выражение ошибки регулирования. Причем эта ошибка может быть представлена в виде двух составляющих: - установившаяся ошибка (точность поддержания регулируемой величины в установившемся режиме); - переходная ошибка (определяет качество регулирования в переходном режиме). Установившаяся ошибка регулирования:
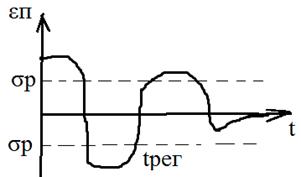
ПРЯМЫЕ ПОКАЗАТЕЛИ КАЧЕСТВА Переходная составляющая ошибки определяется при единичном ступенчатом воздействии:
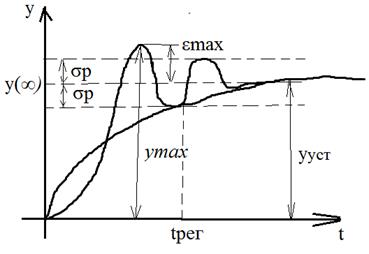
Колебательный процесс наиболее характерен для большинства быстродействующих систем. При этом регулирующая величина может переходить через новое установившееся значение в сторону противоположную начальному значению величины (перерегулирование). Показатели качества: 1) Максимальное перерегулирование – отношение разности между максимальным и установившимся значением регулируемой величины к её установившемуся значению в процентах.
В системах поддерживающих регулируемую величину при изменении внешних воздействий 2) Время регулирования – промежуток t от момента возникновения возмущений до момента, когда абсолютное значение переходной погрешности становится меньше некоторого заданного значения. 3) Число колебаний регулируемой величины за время переходного процесса. Прямые показатели качества наиболее достоверно характеризуют динамические свойства системы. Недостатки: 1) Сложность получения переходной характеристики 2) Отсутствие явных аналитических зависимостей между показателями качества и показателями системы. Поэтому наряду с прямыми широко используются косвенные методы.
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 440; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.108.47 (0.011 с.) |





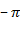 соответствует отрицательное значение ЛАЧХ и соответственно наоборот.
соответствует отрицательное значение ЛАЧХ и соответственно наоборот. - соответственно расстояние от оси абсцисс до ЛАЧХ, но в логарифмическом масштабе. Особыми точками являются точки пересечения АФЧХ с окружностью единичного радиуса. Частоты при которых это происходит называют частотами среза
- соответственно расстояние от оси абсцисс до ЛАЧХ, но в логарифмическом масштабе. Особыми точками являются точки пересечения АФЧХ с окружностью единичного радиуса. Частоты при которых это происходит называют частотами среза 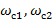 .
.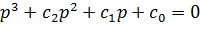






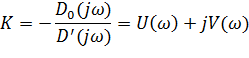








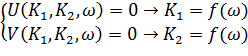
 получили численные значения K1 и K2 и строят в этих координатах границу D-разбиения.
получили численные значения K1 и K2 и строят в этих координатах границу D-разбиения.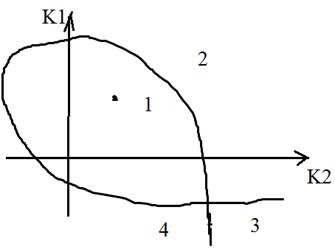








 , а потом поворачивают каждую его точку по часовой стрелке на угол
, а потом поворачивают каждую его точку по часовой стрелке на угол  .
.
 , пока годограф разомкнутой системы не пройдет через критическую точку пока
, пока годограф разомкнутой системы не пройдет через критическую точку пока  и система не окажется на границе устойчивости. При больших запаздываниях устойчивость теряется.
и система не окажется на границе устойчивости. При больших запаздываниях устойчивость теряется.

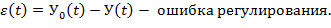
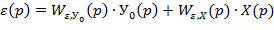


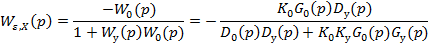
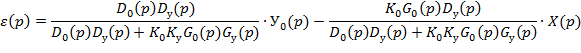
 Установившаяся ошибка при постоянном ступенчатом воздействии называется статической ошибкой и для её определителя используется предельная теорема:
Установившаяся ошибка при постоянном ступенчатом воздействии называется статической ошибкой и для её определителя используется предельная теорема: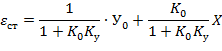
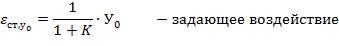
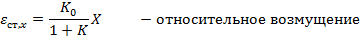
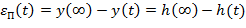
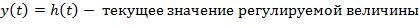
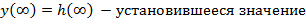
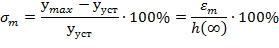
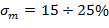
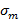 может быть больше.
может быть больше.


