
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Структурная схема САУ напряжения синхронного генератораСодержание книги
Поиск на нашем сайте
1) Синхронный генератор представляется инерционным звеном
Передаточная функция отражает диф. уравнение, которое связывает приращение ЭДС генератора и приращение ЭДС на обмотке возбуждения. 2) Возбудитель
3) Усилитель Уровень выходного напряжения усилителя пропорционален с некоторой задержкой уровню входного сигнала.
4) Измерительный орган
ПОНЯТИЕ УСТОЙЧИВОСТИ И ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ Устойчивость – это способность системы возвращаться в предшествующее установившееся состояние после внезапного изменения внешних воздействий. Различают устойчивость “в малом” (статическая устойчивость); “в большом” (динамическая устойчивость).
Поведение любой системы описывается линейно или линеаризовано к диф. уравнению, решение которого относительно одной из переменных может быть записано следующим образом:
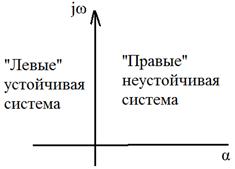
где p – корень характеристического уравнения. САР будет устойчива, если все корни характеристического уравнения будут вещественными отрицательными, либо комплексными, но с отрицательной вещественной частью.
Критерий устойчивости – это правила, которые позволяют судить о знаках корней характеристического уравнения без его решения. - Алгебраические критерии - Частотные критерии (которые используют частотные хар-ки). По виду характеристического уравнения можно сразу сформулировать необходимый признак устойчивости системы: Если все коэффициенты характеристического уравнения положительны, то это является необходимым условием устойчивости системы. Причем для системы 1 и 2-го порядка положительность коэффициентов является достаточным условием.
КРИТЕРИЙ РАУСА К достоинствам метода относятся простая реализация на ЭВМ, а также простота анализа для систем небольшого (до 3) порядка. К недостаткам можно отнести ненаглядность метода, по нему сложно судить о степени устойчивости, о её запасах.
Число строк в таблице Рауса равняется n+1. В первых двух строках записываются коэффициенты характеристического уравнения в соответствии с их индексами. Коэффициентам с отрицательными индексами соответствуют нули.
Формулировка критерия Рауса: Для устойчивости САР необходимо и достаточно, чтобы коэффициенты 1-го столбца были положительными. Если не все коэффициенты 1-го столбца положительны, то число корней уравнения лежащих в правой полуплоскости равно числу переменных знаков в первом столбце таблицы. Если Диагональные миноры критерия Гурвица могут определяться независимо друг от друга и в этом заключается основное достоинство. Для применения критерия Рауса необходимо постепенное заполнение таблицы, однако для систем высокого порядка объем вычислений оказывается гораздо меньше чем для критерия Гурвица.
КРИТЕРИЙ ГУРВИЦА Достоинством метода является простота, недостатком - необходимость выполнения операции вычисления определителя. Критерий Гурвица позволяет судить об отсутствии правых корней характеристического уравнения по знакам диагональных миноров в определителе Гурвица.
По главной диагонали располагаются коэффициенты характеристического уравнения начиная с an-1 по a0 в порядке убывания. Затем столбцы дополняются коэффициентами характеристического уравнения: вверх – в порядке убывания индексов; вниз – в порядке их увеличения. Члены столбцов с индексами больше чем n и меньше 0 принимаются равными нулю.
Необходимым и достаточным условием отсутствия правых корней является положительность всех корней и диагональных миноров.
Важным условием устойчивости является положительность последнего диагонального минора. КРИТЕРИЙ МИХАЙЛОВА В основу критерия Михайлова положен принцип аргумента, известный из теории функции комплексных элементов.
Вектор
Если pi расположено справа, то поворот будет по часовой стрелке с приращением
Если все корни лежат в левой полуплоскости, то
m корней правое; (n-m) левое.
Т. о. правило аргумента формулируется следующим образом: приращение аргумента вектора На основании принципа аргумента Михайлов сформулировал критерий: для устойчивости САР необходимо и достаточно, чтобы годограф характеристического вектора
КРИТЕРИЙ НАЙКВИСТА Позволяет судить об устойчивости замкнутой системы по её АФЧХ:
-характеристическое уравнение разомкнутой САУ.
- характеристическое уравнение замкнутой САУ. Рассмотрим функцию:
-Отношение характеристического уравнения замкнутой системы к характеристическому уравнению разомкнутой системы.
Определяется разностью приращений аргументов замкнутой и разомкнутой системы. Следовательно, имея АФЧХ разомкнутой системы и применяя правило аргумента по вот этому выражению можно определить устойчивость замкнутой системы. 1) Разомкнутая система устойчива. 2) Разомкнутая система неустойчива.
Для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ устойчивой либо нейтральной, находящейся на границе устойчивости разомкнутой САУ не охватывала точку с координатами (-1;j0). Для устойчивости замкнутой системы необходимо, чтобы АФЧХ неустойчивой разомкнутой системы охватывало 0,5m раз точку с координатами (-1;j0) в положительном направлении, где m – число правых корней.
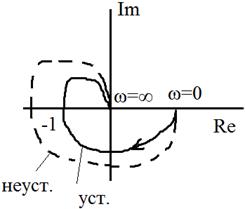
ЗАПАСЫ УСТОЙЧИВОСТИ Частотные запасы устойчивости определяют в соответствии с критерием Найквиста удалением АФЧХ разомкнутой системы от критической точки с координатой (-1;j0).
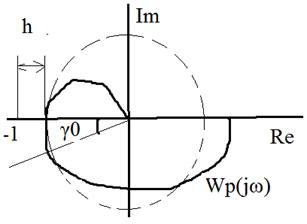
В условиях эксплуатации параметры системы по тем или иным причинам могут изменяться, что может привести к работе системы вблизи критической точки, либо вообще к потере устойчивости. Запас устойчивости h – характеризует удаление годографа от критической точки по отрицательно действительной оси. Обеспечивается крайней неустойчивостью при изменении коэффициента усиления. Второй запас – это запас устойчивости по фазе, определяется углом
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 576; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.76.12 (0.011 с.) |










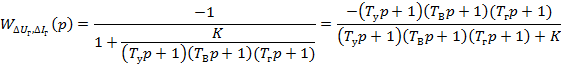

 Объект нейтрален, т.к. после внешнего воздействия он приходит в новое равновесное состояние, которое существенно отличается от предыдущего.
Объект нейтрален, т.к. после внешнего воздействия он приходит в новое равновесное состояние, которое существенно отличается от предыдущего. Объект неустойчив.
Объект неустойчив.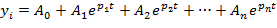
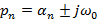
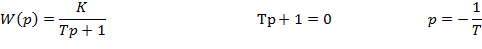



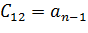

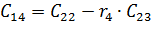

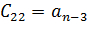
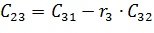
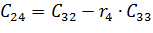

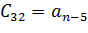
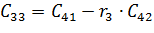 ……………….
……………….

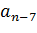 ……
……
……
……
 то это указывает на наличие пары чисто мнимых корней и это будет граница колебательной устойчивости. Если коэффициент a0=0, то в ноль обращается
то это указывает на наличие пары чисто мнимых корней и это будет граница колебательной устойчивости. Если коэффициент a0=0, то в ноль обращается 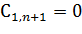 и это будет граница апериодической устойчивости.
и это будет граница апериодической устойчивости.






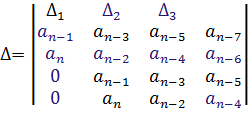





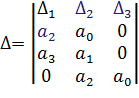
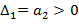
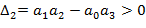
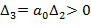
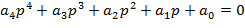






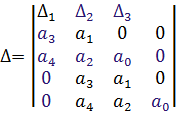

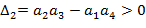
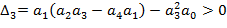
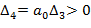
 Если a0=0, то система имен нулевой корень и находится на границе апериодичности устойчивости. Если
Если a0=0, то система имен нулевой корень и находится на границе апериодичности устойчивости. Если 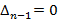 , то система имеет пару мнимых корней и находится на границе колебательной устойчивости.
, то система имеет пару мнимых корней и находится на границе колебательной устойчивости.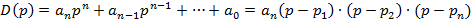

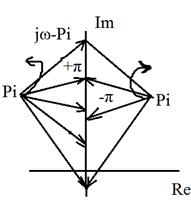
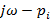 будет перемещаться с положительным направлением (против часовой стрелки) и получим приращение
будет перемещаться с положительным направлением (против часовой стрелки) и получим приращение 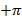 .
.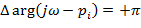
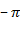 .
.

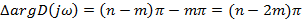
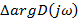 при изменении частоты от
при изменении частоты от  равно разности между чистом (n-m) левых корней и числом m правых корней, умноженных на
равно разности между чистом (n-m) левых корней и числом m правых корней, умноженных на 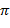 . Т. е. (n-2m)
. Т. е. (n-2m) 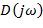 начинаясь при
начинаясь при 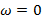 на действительной оси с ростом частоты от 0 до
на действительной оси с ростом частоты от 0 до  обходил последовательно в положительном направлении (против часовой стрелки)
обходил последовательно в положительном направлении (против часовой стрелки) 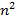 , где n – порядок хар. уравнения.
, где n – порядок хар. уравнения.
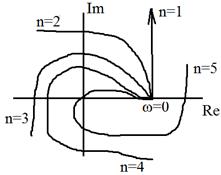
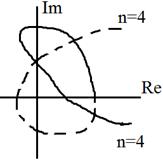 - Годограф для неустойчивой системы:
- Годограф для неустойчивой системы: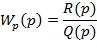


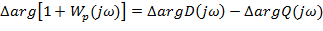



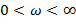
 Запас устойчивости по фазе обеспечивает сохранение устойчивости системы при увеличении запаздывания.
Запас устойчивости по фазе обеспечивает сохранение устойчивости системы при увеличении запаздывания.


