
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятия об управлении и системах управления.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ УПРАВЛЕНИЯ. ПРИНЦИПЫ УПРАВЛЕНИЯ Понятия об управлении и системах управления. Составляющие процесса управления Под управлением будем понимать совокупность мероприятий по организации процесса для достижения поставленной цели.
Необходимые составляющие процесса управления рассмотрим на примере движения судна - см. рис. 1.1. Рис. 1.1 Целью процесса управления в данном случае является поддержание объектом управления (ОУ) заданного курса y з. При движении ОУ (судно) подвергается возмущающему воздействию fв (волны, порывы ветра), в результате чего текущий курс y в некоторый момент времени будет отличаться от заданного y з. Информация о цели и о текущем состоянии процесса управления поступает на управляющее устройство (УУ). В УУ сравниваются цель и текущее состояние, оценивается их рассогласовани е Dy и вырабатывается управляющее воздействие m на регулирующий орган ОУ. В данном случае регулирующий орган ОУ – руль; управляющее воздействие m – угол поворота руля. УУ “принимает решение”, то есть вырабатывает управляющее воздействие на основе величины рассогласования и в соответствии с некоторым алгоритмом управления – законом управления. Это управляющее воздействие должно минимизировать рассогласование между целью и состоянием процесса управления с заданной точностью и за требуемое время. Рассмотренный пример содержит все необходимые аспекты, то есть все перечисленные ниже составляющие процесса управления любым объектом. 1. Наличие четко формализованной цели управления. В данном случае это - требуемый курс судна y з, 2. Контроль за текущим состоянием процесса управления. В данном случае это - истиный курс судна y, 3. Сопоставление цели и состояния процесса, оценка рассогласования и принятие решения, то есть выработка управляющего воздействия, 4. Исполнение решения – непосредственное действие на регулирующий орган ОУ. Отсутствие хотя бы одной из перечисленных составляющих или их неправильная организация делают невозможным осуществление процесса управления либо вообще, либо - с достаточно высоким качеством. Для организации процесса управления конкретным объектом помимо УУ необходимы измерительные устройства для получения информации о текущем состоянии, а также усилительно-преобразовательные устройства и исполнительные механизмы, назначением которых является согласование сигналов по физической природе, по мощности и динамическому диапазону. Все эти взаимосвязанные и взаимодействующие функциональные устройства в совокупности с ОУ и образуют систему управления (СУ).
Принципы управления Несмотря на многообразие ОУ, можно сформулировать лишь несколько основополагающих принципов управления. Реализация того или иного принципа управления определяет вид общей структуры СУ.
Независимо от того, как организован процесс управления, в любой СУ должен присутствовать прямой канал передачи управляющего воздействия fу к той выходной координате y, которая должна это управляющее воздействие “воспроизводить” – рис. 1.2. Рис. 1.2 Здесь изображена укрупненная структура; ОУ может содержать усилительные, преобразовательные и другие функциональные звенья. Принципы управления разделяются по способу контроля за текущим состоянием процесса управления. Принцип разомкнутого управления Структура на рис. 1.2 собственно и реализует принцип разомкнутого управления. По-существу, здесь не производится учет текущей информации о состоянии процесса управления. Этот принцип может быть использован только в тех случаях, когда сигнальное возмущающее воздействие fв незначительно, вариации параметров (параметрические возмущения) всех функциональных устройств также малы, математическое описание СУ известно и достоверно, а требования к качеству процесса управления не слишком высоки. Таким образом, использование принципа разомкнутого управления весьма ограничено. Принцип компенсации
При реализации принципа компенсации учет информации о текущем состоянии процесса управления производится путем непосредственного измерения возмущающего воздействия – см. рис. 1.3. Рис. 1.3 Структурной особенностью СУ, реализующих принцип компенсации, является наличие дополнительного пути прохождения возмущающего воздействия на структурной схеме модели системы. Принцип компенсации возмущения используется в тех случаях, когда имеется глобальное (по сравнению с другими) и поддающееся измерению сигнальное возмущение.
Очевидно, что влияние параметрических возмущений и неопределенность параметров операторов функциональных звеньев в данном случае не учитываются, не ослабляются и непосредственно ухудшают качество процесса управления. Поведение систем управления Каждый объект при функционировании должен иметь требуемое поведение. Для нейтрального и, тем более, неустойчивого объекта следует добиться устойчивого поведения. Кроме этого, необходимо обеспечить инвариантность (независимость) или малую чувствительность управляемых координат к сигнальным и параметрическим возмущениям. Например, для рассмотренного в п. 1.4.1 примера электродвигателя может быть сформулировано требование уменьшить до малой величины (быть может, до нуля) отклонение между nхх и n 1 – см. рис. 1.9. Переходный процесс как реакция на изменение входных воздействий также должен заканчиваться за требуемое время и быть достаточно плавным. Для обеспечения требуемого поведения объекта его объединяют с рядом других функциональных звеньев в систему в соответствии с выбранным приципом управления. Такое множество взаимосвязанных звеньев и объекта проявляется при их взаимодействии новым качеством, не присущим отдельно взятому объекту управления – см. подразд. 1.1, 1.2. Реакция любой СУ на входное воздействие определяется двумя составляющими: характеристиками входного воздействия и свойствами собственно самой СУ. На рис. 1.10 представлена реакция некоторой устойчивой СУ на входное управляющее воздействие, которое в момент времени t = 0 изменяется скачком от нуля до величины fу = Const. Можно выделить две составляющие реакции СУ на входной сигнал: переходный режим (переходный процесс) и установившийся режим. Время окончания переходного процесса – время регулирования t Р– определяют как момент последнего вхождения в некоторую зону. Обычно ее определяют как
Рис. 1.10 Установившаяся ошибка eуст = fy - yуст характеризует точность СУ в установившемся режиме. Динамика СУ (переходный режим) характеризуется быстродействием системы и склонностью процесса к колебательности. Склонность к колебательности оценивается перерегулированием
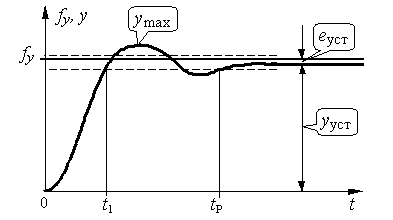
Если под быстродействием понимать скорость изменения выходной координаты при реакции на входное воздействие, то может быть также использован показатель качества время первого согласования t 1, то есть время первого вхождения в зону 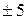 % от установившегося значения yуст. Очевидно, что для процессов с перерегулированием s < 5%, выполняется t P= t 1. Для s ³ 5% имеем t P> t 1. % от установившегося значения yуст. Очевидно, что для процессов с перерегулированием s < 5%, выполняется t P= t 1. Для s ³ 5% имеем t P> t 1.
Рис. 1.11 Рис. 1.12 При значительной колебательности переходного процесса показатели динамики t 1 и t Pнаходятся в противоречии, то есть для достаточно быстродействующей системы время окончания процесса может быть значительным по сравнению с временем первого согласования – см. рис. 1.11. Для процессов в СУ, находящихся на границе устойчивости, время регулирования (то есть время окончания процесса) t P=µ. Для процессов в неустойчивых СУ рассмотренные показатели качества динамики смысла вообще не имеют. Если переходный процесс не имеет перерегулирования, то есть s = 0, то процесс называется апериодическим – см. рис. 1.12.
Задачи теории управления Основные задачи теории управления – анализ и синтез. Анализ направлен на выявление свойств поведения СУ и оценку этих свойств с использованием различных критериев – показателей качества. Кроме констатации свойств СУ анализ должен также объяснять зависимость свойств и характеристик от организации системы (ее внутренней структуры) и от операторов и параметров отдельных звеньев. Синтез направлен на формирование структуры системы для реализации выбранного принципа управления, формирование алгоритма управляющего устройства и определение и расчет операторов звеньев для обеспечения требуемого поведения СУ. СИСТЕМ УПРАВЛЕНИЯ В разделе рассматриваются различные формы представления конечномерных линейных непрерывных стационарных детерминированных моделей СУ. В зависимости от информативности о внутренней организации СУ (о ее структуре), выделяют два типа моделей.
Модели первого типа – со “свернутой” внутренней организацией или модели “ вход-выход ” – см. рис. 2.1. Рис. 2.1 В таких моделях отсутствует информация о внутренней структуре СУ, то есть о составе функциональных звеньев и переменных и о взаимосвязях между ними. Модель представляет собой заданный в некоторой форме математический оператор преобразования входного сигнала f (управляющего или возмущения) в выходной сигнал y. На таких моделях и рассматриваются в данном разделе формы представления оператора перобразования w. Модели второго типа – с раскрытой внутренней организацией – несут информацию о структуре системы – см. подразд. 2.5, 2.6. Дифференциальные уравнения Дифференциальное уравнение (ДУ) “ n -го порядка” связывает между собой во временной области входную переменную f (t), выходную переменную y (t) и их производные:
Порядок n определяется по наибольшему номеру производной левой части уравнения. ДУ дополняется начальными условиями Часто используется компактная запись ДУ, для чего вводится символьный оператор дифференцирования по времени p º d / dt: A (p) y (t) = B (p) f (t), (2.2) где Передаточные функции По определению передаточная функция (ПФ) представляет собой оператор, равный отношению изображения выходной координаты к изображению входной координаты при нулевых начальных условиях. Таким образом, для представленной на рис. 1.1 СУ, ПФ
Здесь и в дальнейшем будем обозначать изображения функций прописными буквами. ПФ может быть легко получена из ДУ (2.1). Для этого преобразуем по Лапласу левую и правую части (2.1); при этом воспользуемся свойством линейности преобразования Лапласа и тем его свойством, что дифференцированию оригинала соответствует умножение изображения на комплексный аргумент s (справледливо при нулевых начальных условиях).
Таким образом, если В результате получим:
С учетом (2.3)
Таким образом, ПФ является дробно-рациональной функцией (отношением двух полиномов). Полиномы числителя и знаменателя образуются из соответствующих коэффициентов правой и левой частей исходного ДУ (2.1) или (2.2). Полином An (s) знаменателя ПФ системы (или отдельного звена) называется характеристическим полиномом системы (звена). Как видно из (2.1) и (2.5), по ДУ можно сразу записать ПФ, и - наоборот. Форма представления ПФ (2.5) называется полиномиальной. Можно представить ПФ также в факторизованной форме, то есть коэффициентом, множеством нулей (корней полинома числителя) zj: j =1,…, m, и множеством полюсов (корней полинома знаменателя) pi: i =1,…, n:
Здесь k = bm / an – отношение старших коэффициентов полиномов (2.5). Временные характеристики Реакция любой динамической системы на входной сигнал – временная характеристика – определяется двумя составляющими: параметрами сигнала и свойствами собственно самой системы. Для рассматриваемых здесь СУ, описываемых линейными дифференциальными уравнениями (2.1), это обстоятельство проявляется в форме решения ДУ, использующей операторный метод на основе преобразования Лапласа. Как следует из (2.3), изображение выходной координаты Y (s)= F (s) W (s). Тогда оригинал – решение ДУ – может быть получен применением обратного преобразования Лапласа: y (t) = L -1{ Y (s)}. (2.7) Решение ДУ может быть сведено у сумме двух составляющих: y (t) = yсв (t) + yвын (t). (2.8) Свободная составляющая yсв (t) характеризует динамику собственно самой системы и определяется решением однородного уравнения, образующегося из (2.1) приравниванием нулю правой части. При этом решение определяется корнями si: i =1,…, n характеристического полинома (или, что тоже самое, полюсами ПФ) системы:
Вынужденная составляющая определяется уже с учетом входного сигнала. В подразд.1.4 введено понятие устойчивости ОУ и СУ с позиции их поведения. Теперь можно записать, что для устойчивости СУ должно выполняться
Если все n корней характеристического полинома действительные, то yсв (t) представляет собой сумму n экспонент - см. (2.9). Если среди корней имеются пары комплексно-сопряженных корней то каждой такой паре si,i+ 1=a±jw в переходном процессе соответствует составляющая Cie a t Cos(w t). Если расположить все корни характеристического полинома на комплексной плоскости, то с учетом (2.10) можно сформулировать следующее утверждение. Частотные характеристики Частотные характеристики (ЧХ) представляют собой зависимости установившихся реакций системы (объекта) на гармонические сигналы всех частот. Если на вход некоторой линейной устойчивой СУ подать сигнал Af Sin(w it), то на ее выходе после окончания переходного процесса установятся вынужденные движения, которые также будут представлять собой гармонический сигнал Ay (w i)Sin(w it+ j(w i)) той же частоты, но измененной амплитуды и сдвинутый по фазе. Отношение Ay (w i)/ Af представляет собой коэффициент передачи по амплитуде на данной частоте R (w i), который называется модулем ЧХ.
В ЧХ, используемых для расетов СУ, частота w - круговая; имеет размерность рад/с (иногда условно обозначается “с-1”). ЧХ может быть описана оператором W (j w) – комплексной функцией вещественного аргумента w. В соответствии с различными формами представления комплексных чисел используют различные типы ЧХ: W (j w)=Re(w)+ j Im(w)= R (w) ej j(w). (2.14) Амплитудно-фазовая характеристика (АФХ) W (j w)=Re(w)+ j Im(w) есть сумма вещественной и мнимой частей ЧХ и строится на комплексной плоскости. При изменении частоты w от нуля до µ конец вектора описывает на комплексной плоскости траекторию, называемую годографом Найквиста. Отдельной оси частот АФХ не имеет и каждая точка характеристики может быть оцифрована соответствующим значением частоты. Амплитудно-частотная характеристика (АЧХ) R (w), где
представляет собой зависимость модуля ЧХ от частоты. Часто используются логарифмические амплитудно-частотные характеристики (ЛАЧХ) L (w) = 20 lg R (w), (2.16) где L (w) – логарифмический модуль, измеряемый в децибеллах (дБ). При делении оси частот на декады (интервалы десятикратного изменения частоты) и распределении w внутри интервалов в логарифмическом масштабе, ЛАЧХ преобретают ряд специфических особенностей, облегчающих их построение и позволяющих более наглядно отображать свойства СУ. Фазо-частотная характеристика (ФЧХ) j(w), где
Как правило, ФЧХ строится одновременно с АЧХ или ЛАЧХ на единой шкале частот; именно соотношение амплитудной и фазовой характеристик позволяет выявить ряд важных свойств СУ. Если известна ПФ W (s) отдельного звена или всей СУ, то частотный оператор получается простой заменой переменной
Так как ПФ является отношением двух полиномов комплексного аргумента s, то при подстановке конкретного значения частоты четные степени полиномов дают вешественные части, а нечетные степени – мнимые части ЧХ. Путем избавления от иррациональности в знаменателе ПФ, могут быть выделены вешественная и мнимая части ЧХ, а затем отдельно модуль и фаза. ПФ по управлению ПФ Ф(s) = Y (s) / F (s). Для получения этого оператора по модели, изображенной на рис. 2.3, необходимо исключить координату E (s): Y (s) = E (s) W Р(s) = (F (s)- Y (s)) W Р(s). (2.20) Из (2.20) получаем
Выразим теперь ПФ замкнутой системы по управлению через полином числителя и знаменателя ПФ разомкнутой системы. Подставляя в (2.21) W Р(s) = B Р(s) / A Р(s), получим
Таким образом, числители ПФ разомкнутой и ПФ по управлению замкнутой систем совпадают. Знаменатель ПФ замкнутой системы A (s), он же - характеристический полином замкнутой системы, равен сумме полиномов знаменателя и числителя ПФ разомкнутой системы. ПФ по ошибке ПФ Фe(s) = E (s) / F (s). Для получения этого оператора по модели, изображенной на рис. 2.3, необходимо исключить координату Y (s): E (s) = F (s) -Y(s) = F (s) - E (s) W Р(s). (2.23) Из этого соотношения получаем
Выразим теперь ПФ замкнутой системы по ошибке через полином числителя и знаменателя ПФ разомкнутой системы. Подставляя в (2.24) W Р(s) = B Р(s) / A Р(s), получим
Таким образом, числитель ПФ замкнутой системы по ошибке совпал со знаменателем ПФ разомкнутой системы. Знаменатель ПФ замкнутой системы A (s), он же - характеристический полином замкнутой системы, также равен сумме полиномов знаменателя и числителя ПФ разомкнутой системы. Сразу обобщим важную особенность. У некоторой СУ - один характеристический полином; он не зависит от назначенных входа и выхода при получени конкретной ПФ. Соотношения (2.21), (2.22) и (2.24), (2.25) справедливы для рассматриваемой здесь типовой СУ, то есть для одноконтурной системы с единичной отрицательной обратной связью.
Пропорциональное звено Уравнение имеет следующий вид y = Kx. (3.1) Передаточная функция W (s) = K /1= K. (3.2) Описывающее это звено алгебраическое уравнение (3.1) можно рассматривать как вырожденное дифференциальное уравнение нулевого порядка. Во временной области это звено воспроизводит любой входной сигнал, изменяя его величину в K раз. В связи с этим такое звено наывается также безынерционным. Единственный параметр K называется “коэффициентом передачи”. Получим частотный оператор звена:
AЧХ пропорционального звена
Модуль логарифмической ЧХ - ЛАЧХ
ФЧХ определяется выражением
Рассмотрим АФХ, которая определяется выражением (3.3) – см. рис. 3.1.
ЛЧХ определяются выражениями (3.5), (3.6) и приведены на рис. 3.2. ЛАЧХ (часто также используют аббревиатуру “ЛАХ”) представляет собой прямую, параллельную оси частот и проходящую от этой оси на расстоянии 20lg K. Очевидно, что приведенная на рис. 3.2 характеристика построена при значении K =10. ФЧХ от параметра K не зависит и совпадает с осью частот. При K = 0, ЛАХ совпадает с осью частот (20lg(1) = 0 дБ); для K < 1 ЛАХ будет проходить под осью частот.
Рис. 3.2 При изменении коэффициента передачи ЛАХ будет подниматься при увеличении K или опускаться при его уменьшении. Величина D L смещения ЛАХ при изменениии K в D K раз будет составлять D L = 20lgD K (дБ). Например, при увеличении коэффициента передачи в 2 раза ЛАХ звена поднимется на 6 дБ, а при уменьшении в 2 раза опуститься на эту же величину. СИСТЕМ УПРАВЛЕНИЯ
Для анализа и синтеза СУ широко используются частотные характеристики. Частотная область обладает высокой информативностью в плане выявления зависимости свойств и показателей качества СУ от операторов отдельных звеньев и значений их параметров. В подразд. 2.5 приведена типовая структура одноконтурной СУ с единичной отрицательной обратной связью. Будем считать, что прямой канал передачи управляющего воздействия образован последовательным соединением типовых звеньев, рассмотренных в разд. 3. Ряд важных свойств замкнутых СУ может быть выявлен при анализе и сформирован при синтезе по частотным характеристикам разомкнутых систем, то есть по оператору прямого канала без обратной связи. Целью данного раздела является описание процесса построения ЧХ СУ без использования компьютера, так как это позволяет установить влияние оператора каждого звена на вид ЧХ и, в конечном счете, на свойства всей СУ. Построение ЛАХ На рис. 4.2. построены асимптотческие ЛАХ Li (w), i =1, 2, 3, 4 отдельно каждого звена, а также ЛАХ L P(w)последовательного соединения.
Рис. 4.2 ЛАХ пропорционального звена L 1(w) проходит параллельно оси частот на расстоянии 20lg K 1= 20lg40 = 20lg(10*2*2) = 20дБ + 6дБ + 6дБ = = 32дБ. ЛАХ интегратора L 2(w) представляет собой прямую с наклоном -20дБ/дек, которая пересекает ось частот при w = 0.2 рад/с. Асимптотическая ЛАХ L 3(w) апериодического звена с ПФ W 3(s) слева от частоты сопряжения 1/ T 1=1 рад/с проходит параллельно оси частот на расстоянии 20lg K 3= 20lg5 = 20lg(10/2) = 20lg(10) - 20lg(2) = 20 дБ - 6 дБ = 14 дБ; справа от линии сопряжения имеет наклон -20дБ/дек. Асимптотическая ЛАХ L 4(w) апериодического звена с ПФ W 4(s) слева от частоты сопряжения 1/ T 2=1 рад/с проходит параллельно оси частот на расстоянии 20lg K 4= 20lg(0.25) = 20lg((1/2)*(1/2)) = (- 6 дБ) + (- 6 дБ) = -12 дБ; справа от линии сопряжения имеет наклон -20дБ/дек. Сумма этих четырех асимптотических ЛАХ L P(w) представляет собой асимптотическую ЛАХ разомкнутой системы, то есть ЛАХ последовательного соединения всех звеньев прмого канала. На рис. 4.2 приведена и уточненная ЛАХ L P(w) (тонкая линия). Максимальное значение поправки d L (wс) = 2*(-3 дБ) = -6 дБ. Построение ЛФХ ФЧХ пропорционального звена j1(w) = 0 во всем диапазоне частот. ФЧХ интегрирующего звена j2(w) = -p/2 также во всем диапазоне частот. ФЧХ обоих апериодических звеньев совпадают и имеют значение -p/4 на частоте сопряжения wc= 1/ T 1= 1/ T 2=1 рад/с. Результирующая ФЧХ jP(w) для рассматриваемого примера представляет собой смещенную на -p/2 удвоенную характеристику апериодического звена с wc= 1 рад/с. На частоте сопряжения в данном случае имеем фазовый сдвиг jP(wc) = (-p/2) + 2*(-p/4) = -p. Пример построения ЛЧХ астатической системы управления Рассмотрим подробно процесс построения ЛЧХ по предложенному в подразд. 4.2 алгоритму для СУ, имеющей ПФ
Рис. 4.4 Проводим линии сопряжения на частотах wc1=1/ T 1= 0.002 рад/с, wc2=1/t1= 0.05 рад/с, wc3=1/ T 2=1/ T 3= 5 рад/с и помечаем их. На шкале частот эти значения отмечены треугольными метками – острием вверх на частоте, равной значению нуля 1/t1, и острием вниз на частотах, равных значениям полюсов 1/ Ti. Направления этих треугольных меток показывают, в какую сторону будет происходить “излом” асимптотической ЛАХ. Для диапазона частот w £ wc,min= wc1=1/ T 1= 0.002 рад/с строим участок ЛАХ, соответствующий сомножителю 10/ s. Слева от wc1сразу проводим сплошную линию; ее продолжение штриховой линией до w =10 рад/с используется только для построения ЛАХ интегратора. Частота wc1“помечена полюсом”, поэтому справа от нее (то есть в сторону увеличения частоты) наклон измениться на -20 дБ/дек и будет составлять -40 дБ/дек. Прямую с таким наклоном следует провести до wc2. Частота wc2“помечена нулем”, поэтому справа от нее наклон измениться на +20 дБ/дек и будет составлять -20 дБ/дек. Этот наклон следует сохранить до wc3. Частота wc3помечена сразу двумя полюсами; справа от нее наклон измениться на 2*(-20 дБ/дек) и будет составлять -60 дБ/дек. Этот наклон останется неизменным при w®µ. На рис. 4.4 показаны ЛАХ звеньев 1/(Tis +1) и 1/(t js +1). Видно, что каждое такое звено имеет модуль 0 дБ слева от своей частоты сопряжения; прибавление его характеристики на w £ wcне изменяет ранее сформированного участка ЛАХ соединения. Справа от своей частоты сопряжения такое звено “срабатывает”, изменяя наклон асимптотической ЛАХ соединения. ФЧХ j P(w) формируется путем построения ФЧХ отдельных звеньев и последующего их суммирования – см. рис. 4.4. Пример построения ЛЧХ статической системы управления Проведем построение ЛЧХ для статической СУ, имеющей ПФ
Построение ЧХ отображено на рис. 4.5. После оцифровки оси частот и нанесения на сетку ЛАХ вертикальных штриховых линий сопряжения начинается построение собственно ЛАХ L P(w). Слева от минимаьной частоты сопряжения wc,min= wc1=1/ T 1= 0.01 рад/с, определяемой самой большой постоянной времени в СУ, формируем низкочастотный участок ЛАХ. В данном случае это прямая, параллельная оси частот и проходящая на расстоянии 20lg(200) = 20lg(10*10*2) = 20lg(10) + 20lg(10) + 20lg(2) = = 20дБ + 20дБ + 6дБ = 46дБ.
Рис. 4.5 Линия сопряжения wc1соответствует полюсу 1/ T 1. Поэтому переход через нее асимптотической ЛАХ в стороу увеличения частоты сопровождается изменением наклона на –20 дБ/дек. Прямую с таким наклоном проводим до следующей частоты сопряжения wc2= 0.2 рад/с, которая соответствует нулю 1/t1, и переход через нее асимптотической ЛАХ в стороу увеличения частоты сопровождается изменением наклона на +20 дБ/дек. В результате суммарный наклон следующего участка ЛАХ будет составлять 0 дБ/дек; параллельный оси частот участок ЛАХ следует продолжить до частоты сопряжения wc3= 4 рад/с. На линии сопряжения этой частоты “срабатывают” два полюса, так как “включаются” два апериодических звена с одинаковыми постоянными времени. Переход через эту линию сопровождается изменением наклона на 2*(-20 дБ/дек) = -40 дБ/дек. В результате окончательный наклон ЛАХ справа от wc3= 4 рад/с равен -40 дБ/дек. ФЧХ j P(w) формируется путем построения ФЧХ отдельных звеньев и последующего их суммирования – см. рис. 4.5. Пример построения ЛЧХ реального дифференцирующего звена Идеальное дифференцирующее звено (см. подразд. 3.3) имеет равномерно возрастающий модуль R (w) во всем диапазоне частот w Î [0,µ); при w ® µ, модуль R (w) ® µ. Такая идеальная модель звена может соответствовать реальности только в ограниченном диапазоне частот. В связи с этим часто используют так называемое реальное дифференцирующее звено, у которого, начиная с некоторой частоты, рост модуля R (w) ограничивается. ПФ такого звена
можно рассматривать как ПФ последовательного соединения двух ранее рассмотренных типовых звеньев – идеального дифференцирующего и апериодического первого порядка (4.5).
На рис. 4.6 представлено построение ЛАХ реального дифференцирующего звена с K = 0.1 и T = 0.25 с. Рис. 4.6 Единственная частота сопряжения wc=1/ T = 4 рад/с определяется апериодическим звеном 1/(T s+1) = 1/(0.25s+1). До частоты сопряжения wc=1/ T наклон ЛАХ определяется наличием дифференциатора и составляет +20 дБ/дек; этот участок ЛАХ (в данном случае – его продолжение за wc) пересечет ось частот при w =1/ K =10 рад/с. На частоте сопряжения wc“включается” асимптотическая ЛАХ апериодического звена, изменяя имеющийся слева от wcнаклон на -20 дБ/дек. В результате получаем суммарный наклон ЛАХ справа от частоты сопряжения, равный 0 дБ/дек и при w Î [wc,µ) ЛАХ будет параллелен оси частот. Результирующая ФЧХ j(w) представляет собой ФЧХ апериодического звена, смещенную на +p/2, так как такой фазовый сдвиг вносит идеальное дифференцирующее звено во всем диапазоне частот – см. рис. 4.6. Систем управления Продолжим рассмотрение примера из подразд. 5.1. Переходная характеристика апериодического звена является экспонентой со временем окончания процесса t р= 3 T (см. п. 1.4.2 и подразд. 3.4). В этом случае:
В выражении (5.3) коэффициент d связывает быстродействие системы с ее частотной полосой пропускания; в данном случае d = 3. Экспонента является апериодическим процессом; время первого согласования t 1, характеризующее быстродействие, и время регулирования t р, т. е. время окончания процесса, совпадают (см. подразд. 1.4). Таким образом, полоса пропускания wпи быстродействие системы находятся в обратно-пропорциональной зависимости – см. рис. 5.3.
Рис. 5.3 На рис. 5.3, а показана АЧХ замкнутой системы при K = 1 – кривая 1. Эта ЧХ соответствует апериодическому звену Ф(s) = 1/(T s+1), T = 1c). В отличие от рассмотренных ранее ЧХ, в данном случае построены не логарифмические АЧХ R (w). При K = 1 имеем wп= 1рад/с. На рис. 5.3, б, построена переходная характеристика замкнутой системы при K = 1 - кривая 1. Время процесса t р1= 3/wп1= 3с. Увеличим в два раза усиление в прямом канале системы, то есть положим K = 2. При этом ЛАХ L Р(w) (прямая с наклоном –20 дБ/дек) поднимется на 6 дБ, в результате чего получим wср= wc= wп= 2 рад/с. Этому будет соответствовать кривая 2 на АЧХ (рис. 5.3, а) с увеличенной в два раза полосой пропускания. Время переходного процесса наоборот уменьшится в два раза: t р2= 3/wп2= 1.5 с – кривая 2 на рис. 5.3, б. Уменьшим в два раза усиление в прямом канале системы, то есть положим K = 0.5. При этом ЛАХ L Р(w) опустится на 6 дБ (относительно исходной ситуации при K = 1) и wср= wc= wп= 0.5 рад/с. Этому соответствует кривая 3 на АЧХ (рис. 5.3, а) с уменьшенной в два раза полосой пропускания. Время переходного процесса наоборот увеличится в два раза: t р3= 3/wп3= 6с. Заметим, что быстродействие системы мы изменяли не за счет варьирования какой-либо инерционности (постоянной времени). В исходной системе – рис. 5.1, W Р(s) = K / s - такого параметра вообще не присутствует. Полоса пропускания, а следовательно, и быстродействие, обеспечивались усилением в прямом канале системы. Так как рассматриваем СУ с единичной обратной связью, то это усиление совпадает с контурным усилением, то есть коэффициентом передачи контура обратной связи. Примеры сопоставления частотных и временных Система управления Модель СУ приведена в подразд. 4.3. Оператор W Р(s) задан выражением (4.3). На рис. 4.4 подробно отображены ЛЧХ и процесс их построения. На рис. 5.4 показаны ЛЧХ разомкнутой и замкнутой СУ. Видно, что в диапазоне частот, где усиления в разомкнутом контуре большие, ЧХ разомкнутой и замкнутой систем существенно различаются; модуль ЧХ замкнутой системы R (w)»1 (L (w)» 0 дБ). На частотах, где L Р(w) < 0, ЧХ разомкнутой и замкнутой систем совпадают – обратная связь здесь “не работает”.
wср= 0.74 wп. (5.4) Переходная характеристика СУ приведена на рис. 5.5. Заметим, что время окончания процесса t рпревосходит время первого согласования t 1почти в пять раз. Оценим коэффициент, связывающий быстродействие и полосу пропускания для этой системы:
Некоторое отклонение значения коэффициента d = 2.6 от приведенного в (5.3) объясняется отличием вида переходного процесса от экспоненты – см. рис. 5.5.
Модель СУ приведена в подразд. 4.4. Оператор W Р(s) задан выражением (4.4). На рис. 4.5 подробно отображены ЛЧХ и процесс их построения. На рис. 5.6 показаны ЛЧХ разомкнутой и замкнутой СУ. Видно, что в диапазоне частот, где усиления в разомкнутом контуре большие, ЧХ разомкнутой и замкнутой систем существенно различаются; модуль ЧХ замкнутой системы R (w)»1 (L (w)» 0 дБ). На частотах, где L Р(w) < 0, ЧХ разомкнутой и замкнутой систем совпадают – обратная связь здесь “не работает”. Частота среза разомкнутой системы wср= 12 рад/с. Полоса пропускания замкнутой системы wп= 18.5 рад/с. Переходная характеристика СУ приведена на рис. 5.7. Заметим, что время окончания процесса t рпревосходит время первого согласования t 1почти в 17 раз! Это связано со значи-тельной колебательностью (перерегулирование s = 27%), а также с “затягиванием” приближения координаты к установившемуся значению.
В данном случае значение d = 2.8. Несмотря на значительное отличие процесса от экспоненты, снова получили выражение, близкое к (5.3). Таким образом, с достаточной достоверностью можно оценить быстродействие СУ по ее ЧХ, воспользовшись соотношением
где d» (2.6¸3). 5.4. Синтез систем управления по требованиям К быстродействию | ||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |




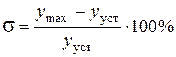 . (1.5)
. (1.5)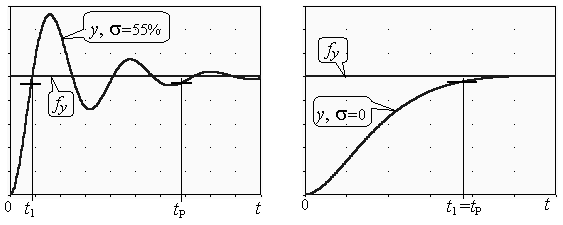

 . (2.1)
. (2.1) .
. - оператор-ные полиномы.
- оператор-ные полиномы. . (2.3)
. (2.3)
 . (2.4)
. (2.4) . (2.5)
. (2.5)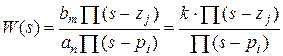 . (2.6)
. (2.6) . (2.9)
. (2.9) . (2.10)
. (2.10) , (2.15)
, (2.15) . (2.17)
. (2.17)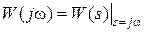 . (2.18)
. (2.18)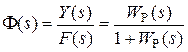 . (2.21)
. (2.21) . (2.22)
. (2.22)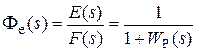 . (2.24)
. (2.24) . (2.25)
. (2.25)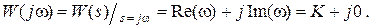 (3.3)
(3.3)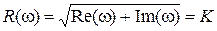 . (3.4)
. (3.4)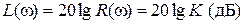 . (3.5)
. (3.5)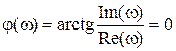 О. (3.6)
О. (3.6) Мнимая составляющая ЧХ равна нулю, а вещественная часть равна K и не зависит от частоты. Поэтому траектория конца вектора ЧХ при изменении частоты от нуля до µ вырождается в точку.
Мнимая составляющая ЧХ равна нулю, а вещественная часть равна K и не зависит от частоты. Поэтому траектория конца вектора ЧХ при изменении частоты от нуля до µ вырождается в точку.

 . (4.3)
. (4.3)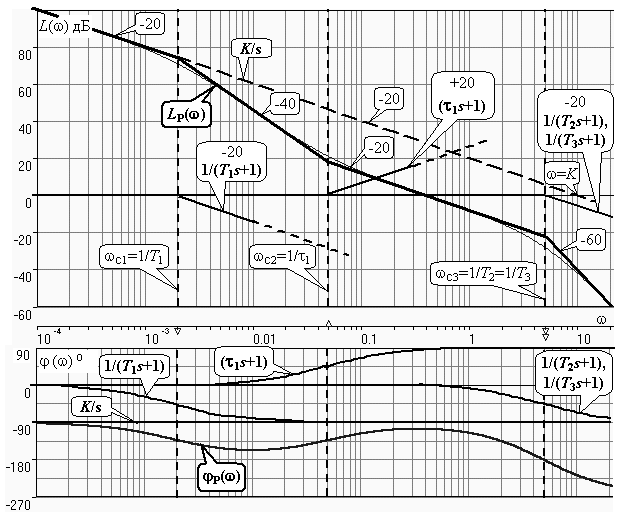
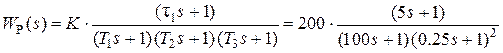 . (4.4)
. (4.4)
 (4.5)
(4.5)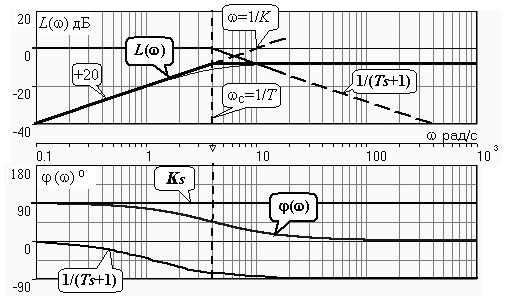
 (с). (5.3)
(с). (5.3)
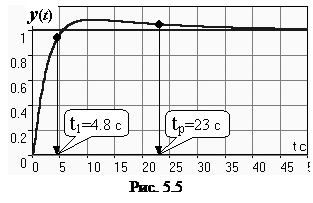 Частота среза разомкнутой системы wср= 0.4 рад/с. Полоса пропускания замкнутой системы wп= 0.54 рад/с. Отметим, что для рассматриваемой системы частоты wсри wпсвязаны соотношением:
Частота среза разомкнутой системы wср= 0.4 рад/с. Полоса пропускания замкнутой системы wп= 0.54 рад/с. Отметим, что для рассматриваемой системы частоты wсри wпсвязаны соотношением: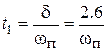 (с). (5.5)
(с). (5.5)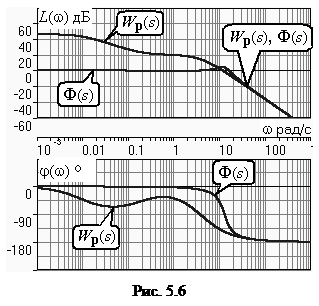 5.3.2. Статическая система управления
5.3.2. Статическая система управления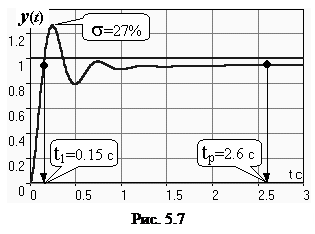 Оценим коэффициент d для этого процесса:
Оценим коэффициент d для этого процесса: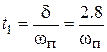 (с). (5.6)
(с). (5.6)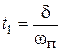 (с), (5.7)
(с), (5.7)


