
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типовое поведение систем управленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Несмотря на многообразие объектов различного функционального назначения и систем управления этими объектами, можно описать типовое поведение некоторой “хорошей” СУ. Переходнвй процесс в такой системе должен быть плавным и либо апериодическим, либо слабоколебательным – см. рис. 1.13. Ограничение на допустимое перерегулирование зависит от требований к конкретной СУ; обычно s < 10 ¸15%. Для некоторых систем перерегулирование вообще недопустимо, то есть СУ должна иметь апериодический переходный процесс.
Задачи теории управления Основные задачи теории управления – анализ и синтез. Анализ направлен на выявление свойств поведения СУ и оценку этих свойств с использованием различных критериев – показателей качества. Кроме констатации свойств СУ анализ должен также объяснять зависимость свойств и характеристик от организации системы (ее внутренней структуры) и от операторов и параметров отдельных звеньев. Синтез направлен на формирование структуры системы для реализации выбранного принципа управления, формирование алгоритма управляющего устройства и определение и расчет операторов звеньев для обеспечения требуемого поведения СУ. ЛИНЕЙНЫЕ МОДЕЛИ И ХАРАКТЕРИСТИКИ СИСТЕМ УПРАВЛЕНИЯ В разделе рассматриваются различные формы представления конечномерных линейных непрерывных стационарных детерминированных моделей СУ. В зависимости от информативности о внутренней организации СУ (о ее структуре), выделяют два типа моделей.
Модели первого типа – со “свернутой” внутренней организацией или модели “ вход-выход ” – см. рис. 2.1. Рис. 2.1 В таких моделях отсутствует информация о внутренней структуре СУ, то есть о составе функциональных звеньев и переменных и о взаимосвязях между ними. Модель представляет собой заданный в некоторой форме математический оператор преобразования входного сигнала f (управляющего или возмущения) в выходной сигнал y. На таких моделях и рассматриваются в данном разделе формы представления оператора перобразования w. Модели второго типа – с раскрытой внутренней организацией – несут информацию о структуре системы – см. подразд. 2.5, 2.6. Дифференциальные уравнения Дифференциальное уравнение (ДУ) “ n -го порядка” связывает между собой во временной области входную переменную f (t), выходную переменную y (t) и их производные:
Порядок n определяется по наибольшему номеру производной левой части уравнения. ДУ дополняется начальными условиями Часто используется компактная запись ДУ, для чего вводится символьный оператор дифференцирования по времени p º d / dt: A (p) y (t) = B (p) f (t), (2.2) где Передаточные функции По определению передаточная функция (ПФ) представляет собой оператор, равный отношению изображения выходной координаты к изображению входной координаты при нулевых начальных условиях. Таким образом, для представленной на рис. 1.1 СУ, ПФ
Здесь и в дальнейшем будем обозначать изображения функций прописными буквами. ПФ может быть легко получена из ДУ (2.1). Для этого преобразуем по Лапласу левую и правую части (2.1); при этом воспользуемся свойством линейности преобразования Лапласа и тем его свойством, что дифференцированию оригинала соответствует умножение изображения на комплексный аргумент s (справледливо при нулевых начальных условиях). Таким образом, если В результате получим:
С учетом (2.3)
Таким образом, ПФ является дробно-рациональной функцией (отношением двух полиномов). Полиномы числителя и знаменателя образуются из соответствующих коэффициентов правой и левой частей исходного ДУ (2.1) или (2.2). Полином An (s) знаменателя ПФ системы (или отдельного звена) называется характеристическим полиномом системы (звена). Как видно из (2.1) и (2.5), по ДУ можно сразу записать ПФ, и - наоборот. Форма представления ПФ (2.5) называется полиномиальной. Можно представить ПФ также в факторизованной форме, то есть коэффициентом, множеством нулей (корней полинома числителя) zj: j =1,…, m, и множеством полюсов (корней полинома знаменателя) pi: i =1,…, n:
Здесь k = bm / an – отношение старших коэффициентов полиномов (2.5). Временные характеристики Реакция любой динамической системы на входной сигнал – временная характеристика – определяется двумя составляющими: параметрами сигнала и свойствами собственно самой системы. Для рассматриваемых здесь СУ, описываемых линейными дифференциальными уравнениями (2.1), это обстоятельство проявляется в форме решения ДУ, использующей операторный метод на основе преобразования Лапласа. Как следует из (2.3), изображение выходной координаты Y (s)= F (s) W (s). Тогда оригинал – решение ДУ – может быть получен применением обратного преобразования Лапласа: y (t) = L -1{ Y (s)}. (2.7) Решение ДУ может быть сведено у сумме двух составляющих: y (t) = yсв (t) + yвын (t). (2.8) Свободная составляющая yсв (t) характеризует динамику собственно самой системы и определяется решением однородного уравнения, образующегося из (2.1) приравниванием нулю правой части. При этом решение определяется корнями si: i =1,…, n характеристического полинома (или, что тоже самое, полюсами ПФ) системы:
Вынужденная составляющая определяется уже с учетом входного сигнала. В подразд.1.4 введено понятие устойчивости ОУ и СУ с позиции их поведения. Теперь можно записать, что для устойчивости СУ должно выполняться
Если все n корней характеристического полинома действительные, то yсв (t) представляет собой сумму n экспонент - см. (2.9). Если среди корней имеются пары комплексно-сопряженных корней то каждой такой паре si,i+ 1=a±jw в переходном процессе соответствует составляющая Cie a t Cos(w t). Если расположить все корни характеристического полинома на комплексной плоскости, то с учетом (2.10) можно сформулировать следующее утверждение.
|
|||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 501; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.57 (0.01 с.) |

 Показанные на рис. 1.13 кривые могут быть решением линейного дифференциального уравнения второго порядка, характеристический полином которого имеет пару либо действительных корней (апериодичес-кий процесс), либо – пару слабо-колебательных комплексно-сопря-женных корней (процесс с не большим перерегулированием). Отсюда следует, что при проектированиии даже сложной СУ, содержащей различные динамические звенья и описываемой дифференциальным уравнением достаточно высокого порядка, следует обеспечивать типовое, “простое” поведение, соответствующее поведению системы низкого порядка.
Показанные на рис. 1.13 кривые могут быть решением линейного дифференциального уравнения второго порядка, характеристический полином которого имеет пару либо действительных корней (апериодичес-кий процесс), либо – пару слабо-колебательных комплексно-сопря-женных корней (процесс с не большим перерегулированием). Отсюда следует, что при проектированиии даже сложной СУ, содержащей различные динамические звенья и описываемой дифференциальным уравнением достаточно высокого порядка, следует обеспечивать типовое, “простое” поведение, соответствующее поведению системы низкого порядка.
 . (2.1)
. (2.1) .
. - оператор-ные полиномы.
- оператор-ные полиномы. . (2.3)
. (2.3)
 . (2.4)
. (2.4) . (2.5)
. (2.5)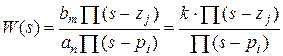 . (2.6)
. (2.6) . (2.9)
. (2.9) . (2.10)
. (2.10)


