Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм построения ЛАХ последовательного соединения типовых звеньевСодержание книги
Поиск на нашем сайте
Как следует из разд. 3 и подразд. 4.1, построение асимптотической ЛАХ последовательного соединения типовых звеньев сводится к суммированию на графике отрезков прямых линий с наклонами, кратными 20 дБ/дек. Используем более эффективный способ построения ЛАХ последовательного соединения звеньев, который не требует построения ЛАХ отдельно каждого звена и последующего суммирования этих ЛАХ. Для рассмотренного в подразд. 4.1. примера представим ПФ W P(s) = W 1(s) W 2(s) W 3(s) W 4(s) в следующем виде
Основным в данном случае является то обстоятельство, что коэффициенты передач всех звеньев сосредоточены в одном (первом) сомножителе 10/ s; оба апериодических звена имеют единичный коэффициент передачи. Очевидно, что результирующая ЛАХ от такого перераспределения параметров должна остаться без изменений. Построим ЛАХ звеньев-сомножителей, представленных в (4.1) – см. рис. 4.3.
Рис. 4.3 Проведем вертикальную штриховую линию сопряжения на частоте wc=1/ T 1= 1/ T 2=1рад/с. Заметим, что нахождение частот сопряжения позволяет оцифровать ось частот. Построим ЛАХ первого сомножителя в (4.1). Для рассматриваемого примера первый сомножитель соответствует интегрирующему звену с коэффициентом передачи K = 10; его ЛАХ представляет собой прямую с наклоном -20дБ/дек, пересекающую ось частот при w =10. От левой границы частотного диапазона до частоты сопряжения wcэтот участок ЛАХ проведем сплошной линией, а справа от wcдо w = K =10 наметим ее штрихами – см. рис. 4.3. Теперь построим ЛАХ звеньев 1/(s+1). Слева от wcасимптотическая ЛАХ этих звеньев проходит по оси частот, так как 20lg(1) = 0 дБ. Очевидно, что характеристики апериодических звеньев с K =1 не изменят при суммировании построенную ранее характеристику интегратора на диапазоне w < wc. На диапазоне частот w > wcсформировавшийся наклон -20дБ/дек будет изменен на 2*(-20) дБ/дек. Продолжение вправо от wcпрямой с наклоном -60дБ/дек образует результирующую асимптотическую ЛАХ всего соединения звеньев – см. рис. 4.3.
Сформируем алгоритм построения ЛАХ последовательного соединения любых типовых звеньев, позволяющий получить характеристику без предварительного построения и суммирования ЛАХ отдельных звеньев. 1. Оператор последовательного соединения звеньев приводится к следующему виду.
n =…-2, -1, 0, 1, 2,…. Первый сомножитель в (4.2) определит наклон низкочастотного участка ЛАХ (слева от крайней левой линии сопряжения). При n = 0 имеем “статическую систему”; наклон низкочастотного участка ЛАХ будет равен 0 дБ/дек, то есть ЛАХ пройдет параллельно оси частот. При n = 1 имеем “систему с астатизмом первого порядка”; наклон низкочастотного участка ЛАХ (будет равен -20 дБ/дек. При n = 2 имеем “систему с астатизмом второго порядка”; наклон низкочастотного участка ЛАХ будет равен -40 дБ/дек. Значениz n = -1 или n = -2 соответствуют наличию в соединении одного или двух идеальных дифференцирующих звеньев; наклон низкочастотного участка ЛАХ будет равен +20 дБ/дек или +40 дБ/дек. 2. На частотной оси помечаются частоты сопряжения; при этом оцифровывается вся шкала частот. Проводятся вертикальные штриховые линии сопряжения. Каждая линия помечается в соответствии со своей постоянной времени 1/ Ti или 1/t j. Важным фактором является четкое разграничение, принадлежит линия сопряжения постоянной времени Ti знаменателя, или постоянной времени t j числителя ПФ. 3. Для диапазона частот w £ wc,min, то есть левее самой левой линии сопряжения, строится ЛАХ сомножителя (K / s n). 4. Далее построение результирующей ЛАХ производится от wc,min вправо, то есть в сторону увеличения частоты. Пересечение ранее сформированного участка ЛАХ с очередной линией сопряжения изменяет наклон ЛАХ на -20 дБ/дек, если линия сопряжения помечена 1/ Ti, или на +20 дБ/дек, если линия сопряжения помечена 1/t j. При этом необходимо иметь ввиду, что постоянные времени некоторых звеньев могут совпадать, как это имеет место в рассмотренном примере подразд. 4.1 и 4.2. В этом случае изменение наклона асимптотической ЛАХ будет иметь величину, кратную 20 дБ/дек. Описанный способ в значительно меньшей степени подвержен возникновению ошибок при построении ЛАХ по сравнению со способом, основанном на построении ЛАХ отдельно каждого звена с последующим суммированием характеристик. Единственным требованием для получения достоверной результирующей ЛАХ является точное соблюдение кратным 20 дБ/дек величин наклонов отрезков асимптотической характеристики. Пример построения ЛЧХ астатической системы управления Рассмотрим подробно процесс построения ЛЧХ по предложенному в подразд. 4.2 алгоритму для СУ, имеющей ПФ
Рис. 4.4 Проводим линии сопряжения на частотах wc1=1/ T 1= 0.002 рад/с, wc2=1/t1= 0.05 рад/с, wc3=1/ T 2=1/ T 3= 5 рад/с и помечаем их. На шкале частот эти значения отмечены треугольными метками – острием вверх на частоте, равной значению нуля 1/t1, и острием вниз на частотах, равных значениям полюсов 1/ Ti. Направления этих треугольных меток показывают, в какую сторону будет происходить “излом” асимптотической ЛАХ. Для диапазона частот w £ wc,min= wc1=1/ T 1= 0.002 рад/с строим участок ЛАХ, соответствующий сомножителю 10/ s. Слева от wc1сразу проводим сплошную линию; ее продолжение штриховой линией до w =10 рад/с используется только для построения ЛАХ интегратора. Частота wc1“помечена полюсом”, поэтому справа от нее (то есть в сторону увеличения частоты) наклон измениться на -20 дБ/дек и будет составлять -40 дБ/дек. Прямую с таким наклоном следует провести до wc2. Частота wc2“помечена нулем”, поэтому справа от нее наклон измениться на +20 дБ/дек и будет составлять -20 дБ/дек. Этот наклон следует сохранить до wc3. Частота wc3помечена сразу двумя полюсами; справа от нее наклон измениться на 2*(-20 дБ/дек) и будет составлять -60 дБ/дек. Этот наклон останется неизменным при w®µ. На рис. 4.4 показаны ЛАХ звеньев 1/(Tis +1) и 1/(t js +1). Видно, что каждое такое звено имеет модуль 0 дБ слева от своей частоты сопряжения; прибавление его характеристики на w £ wcне изменяет ранее сформированного участка ЛАХ соединения. Справа от своей частоты сопряжения такое звено “срабатывает”, изменяя наклон асимптотической ЛАХ соединения. ФЧХ j P(w) формируется путем построения ФЧХ отдельных звеньев и последующего их суммирования – см. рис. 4.4. Пример построения ЛЧХ статической системы управления Проведем построение ЛЧХ для статической СУ, имеющей ПФ
Построение ЧХ отображено на рис. 4.5. После оцифровки оси частот и нанесения на сетку ЛАХ вертикальных штриховых линий сопряжения начинается построение собственно ЛАХ L P(w). Слева от минимаьной частоты сопряжения wc,min= wc1=1/ T 1= 0.01 рад/с, определяемой самой большой постоянной времени в СУ, формируем низкочастотный участок ЛАХ. В данном случае это прямая, параллельная оси частот и проходящая на расстоянии 20lg(200) = 20lg(10*10*2) = 20lg(10) + 20lg(10) + 20lg(2) = = 20дБ + 20дБ + 6дБ = 46дБ.
Рис. 4.5 Линия сопряжения wc1соответствует полюсу 1/ T 1. Поэтому переход через нее асимптотической ЛАХ в стороу увеличения частоты сопровождается изменением наклона на –20 дБ/дек. Прямую с таким наклоном проводим до следующей частоты сопряжения wc2= 0.2 рад/с, которая соответствует нулю 1/t1, и переход через нее асимптотической ЛАХ в стороу увеличения частоты сопровождается изменением наклона на +20 дБ/дек. В результате суммарный наклон следующего участка ЛАХ будет составлять 0 дБ/дек; параллельный оси частот участок ЛАХ следует продолжить до частоты сопряжения wc3= 4 рад/с. На линии сопряжения этой частоты “срабатывают” два полюса, так как “включаются” два апериодических звена с одинаковыми постоянными времени. Переход через эту линию сопровождается изменением наклона на 2*(-20 дБ/дек) = -40 дБ/дек. В результате окончательный наклон ЛАХ справа от wc3= 4 рад/с равен -40 дБ/дек. ФЧХ j P(w) формируется путем построения ФЧХ отдельных звеньев и последующего их суммирования – см. рис. 4.5. Пример построения ЛЧХ реального дифференцирующего звена Идеальное дифференцирующее звено (см. подразд. 3.3) имеет равномерно возрастающий модуль R (w) во всем диапазоне частот w Î [0,µ); при w ® µ, модуль R (w) ® µ. Такая идеальная модель звена может соответствовать реальности только в ограниченном диапазоне частот. В связи с этим часто используют так называемое реальное дифференцирующее звено, у которого, начиная с некоторой частоты, рост модуля R (w) ограничивается. ПФ такого звена
можно рассматривать как ПФ последовательного соединения двух ранее рассмотренных типовых звеньев – идеального дифференцирующего и апериодического первого порядка (4.5).
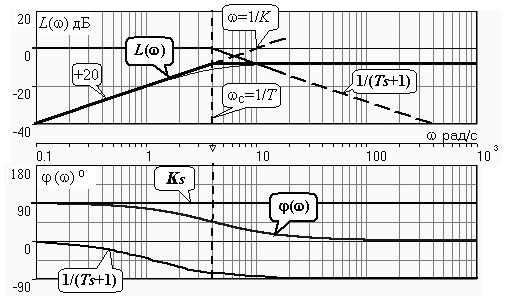
На рис. 4.6 представлено построение ЛАХ реального дифференцирующего звена с K = 0.1 и T = 0.25 с. Рис. 4.6 Единственная частота сопряжения wc=1/ T = 4 рад/с определяется апериодическим звеном 1/(T s+1) = 1/(0.25s+1). До частоты сопряжения wc=1/ T наклон ЛАХ определяется наличием дифференциатора и составляет +20 дБ/дек; этот участок ЛАХ (в данном случае – его продолжение за wc) пересечет ось частот при w =1/ K =10 рад/с. На частоте сопряжения wc“включается” асимптотическая ЛАХ апериодического звена, изменяя имеющийся слева от wcнаклон на -20 дБ/дек. В результате получаем суммарный наклон ЛАХ справа от частоты сопряжения, равный 0 дБ/дек и при w Î [wc,µ) ЛАХ будет параллелен оси частот. Результирующая ФЧХ j(w) представляет собой ФЧХ апериодического звена, смещенную на +p/2, так как такой фазовый сдвиг вносит идеальное дифференцирующее звено во всем диапазоне частот – см. рис. 4.6.
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 817; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.5.179 (0.009 с.) |

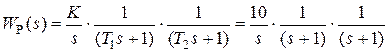 . (4.1)
. (4.1)
 , (4.2)
, (4.2) . (4.3)
. (4.3)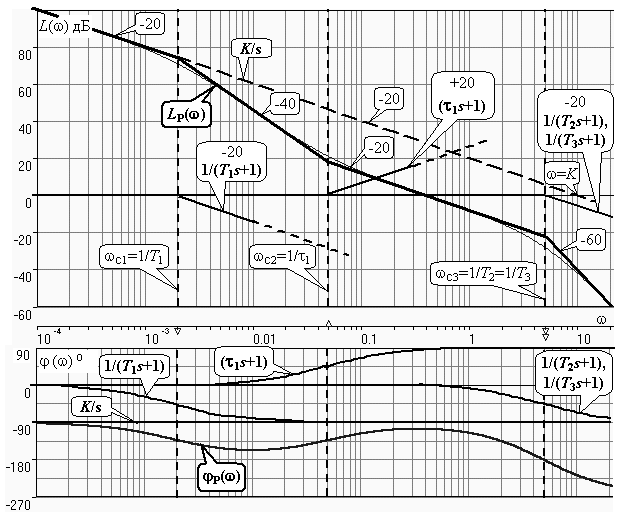
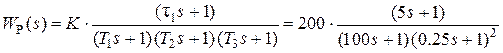 . (4.4)
. (4.4)
 (4.5)
(4.5)