
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Апериодическое звено первого порядкаСодержание книги
Поиск на нашем сайте
Диффенециальное уравнение имеет следующий вид
Передаточная функция
Параметр K называется коэффициентом передачи, T (с) - постоянная времени. Изображение сигнала на выходе звена при подаче на вход единичного ступенчатого воздействия
Обратное преобразование Лапласа дает переходный процесс:
Частотный оператор апериодичес-кого звена:
Для получения AФХ выделим вещественную и мнимую части этой комлексной функции, для чего дробь в (3.23) домножим и разделим на комплексно-сопряженное знаменателю выражение. Выполнив соответствующие преобразования, получим:
Можно показать, что на комплексной плоскости это выражение представляет собой уравнение окружности с центром в точке (Re = K /2, Im = 0).
Используя (3.24), получим выражение для модуля и фазы ЧХ звена:
и
Из этих выражений видно, что на нулевой частоте R (0) = K, j(0) = 0o, то есть апериодическое звено ведет себя как пропорциональное звено. При увеличении частоты модуль монотонно убывает и стремится к нулю, а фазовый сдвиг стремится к –p/2. Модуль ЛАЧХ
ЛЧХ для апериодического звена с параметрами K = 10, T = 1c приведены на рис. 3.10.
Рис. 3.10 Рассмотрим подробно способ построения ЛАЧХ без вычисления множества точек этой характеристики. Определим так называемую частоту сопряжения wс=1/ T. На ЛЧХ проведем вертикальную штриховую линию при значении частоты w = wс(для рассматриваемого примера wс=1 рад/с – см. рис. 3.10). Будем отдельно строить участки ЛАХ для w < wси w > wс. Рассмотрим диапазон низких частот, который для апериодического звена определим как w << wс. При этом, с учетом (3.25) имеем w2 T 2<< 1 и из (3.27) получаем L (w) @ 20lg K – см. рис. 3.10. Проведем прямую линию - асимптоту - параллельно оси частот на расстоянии 20lg K от оси частот влево от штриховой вертикальной линии wс= 1/ T. Теперь рассмотрим диапазон высоких частот w >> wс. При этом имеем w2 T 2>> 1 и из (3.27) получаем L (w) @ 20lg(K/T w) = 20lg((K/T)/w). Последнее выражение соответствует зависимости модуля ЧХ для интегрирующего звена с коэффициентом передачи (K/T) – см. (3.10), (3.11). Его ЛАХ представляет собой прямую линию с наклоном –20 дБ/дек; частота среза для такой характеристики wср= (K/T). На частоте сопряжения имеем L (wс) = 20lg K. В соответствии со сказанным из точки L (wс) = 20lg K в сторону высоких частот проведем прямую линию с наклоном –20 дБ/дек. Полученная ЛАХ, состоящая из двух отрезков прямой линии, которые сопрягаются на частоте wс, называется асимтотической ЛАХ – см. рис. 3.10. Существенные с позиции расчетов отличия точной ЛАХ от асимтотической ЛАХ будут проявляться в окрестности wс, где значения составляющей w2 T 2будут соизмеримы с единицей (см. выражение (3.27)). На рис. 3.10 изображены асимптотическая ЛАХ (тонкие прямые линии) и точная ЛАХ (жирная кривая). Разница d L (w) между точной и асимптотической ЛАХ называется поправкой, которая также изображена на этом рисунке. Максимальное отличие имеет место на частоте сопряжения и составляет d L (wс) @ –3 дБ. На логарифмической ЧХ поправка симметрична относительно линии сопряжения. С достаточной для практических целей точностью можно считать, что d L (w) @ 0 для диапазонов частот w < (wс/3) и w > 3wс. При построении ЛАХ без вычисления точных значений L (w) в этом диапазоне достаточно наметить две точки на асимптотических ЛАХ при w @ (wс/3) и при w @ 3wс, а также смещенную на –3 дБ точку сопряжения асимптот, и соединить эти три точки плавной симметричной линией – см. рис. 3.10. Полученная таким образом уточненная ЛАХ будет иметь достаточную для практических расчетов точность построения. ФЧХ на частоте сопряжения wс=1/ T, как следует из (3.26), имеет значение j(wс) = -45o. Как видно из рис. 3.10, при логарифмическом масштабе оси частот ФЧХ апериодического звена симметрична относительно точки j(wс) = -45o. При смещении на декаду влево от wс=1/ T, имеем j(0.1wс) @ -6o, при смещении на декаду вправо j(10wс) @ -84o. Таким образом, на частотный диапазон [0.1wс, 10wс] приходится основное изменение фазы ЧХ апериодическогог звена. В выражение (3.26) не входит параметр K. При построении ЛАХ в одном и том же масштабе, для любого апериодического звена ЛФЧХ представляет собой одну и ту же кривую, точка j(wс) = -45oкоторой устанавливается под частотной осью на значении wс=1/ T. В операторе звена (3.20) зафиксируем постоянную времени T и будем варьировать коэффициент передачи K. В ЛЧХ не изменится местоположение частоты сопряжения; ФЧХ также останется без изменений. ЛАХ будет смещаться параллельно самой себе: подниматься при увеличении K или опускаться при уменьшении K. Величина смещения ЛАХ D L при изменениии K в D K раз будет составлять D L = 20lg(D K) дБ. Например, при увеличении K в 5 раз ЛАХ поднимется на 14 дБ, а при уменьшении K в 10 раз опуститься на 20 дБ. В операторе звена (3.20) зафиксируем коэффициент передачи K и будем варьировать постоянную времени T, определяющую инерционность апериодического звена. Это вызовет смещение линии сопряжения, проходящей на wс=1/ T. Увеличение T приводит к уменьшению частоты сопряжения и, как следствие, полосы пропускания звена. Переходный процесс будет затягиваться – см. (3.22). Уменьшение T вызывает обратную картину. Параллельный оси частот низкочастотный участок асимптотической ЛАХ (слева от частоты сопряжения) остается без изменений при варьировании постоянной времени T. ФЧХ при изменении постоянной времени T будет смещаться влево при увеличении T, или вправо при его уменьшении, следуя точкой j(wс) = -45oза линией сопряжения на wс=1/ T. Отдельно заметим, что при K = 1 низкочастотный участок асимптотической ЛАХ проходит по оси частот, так как 20lg(1) = 0 дБ. Эта особенность будет использована при построении ЛАХ последовательного соединения типовых звеньев СУ.
|
|||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 348; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.186.233 (0.007 с.) |


 . (3.19)
. (3.19) . (3.20)
. (3.20) . (3.21)
. (3.21) . (3.22)
. (3.22) Таким образом, при реакции на единичное ступенчатое воздействие выходная координата стремится к установившемуся значению K по экспоненциальной зависимости – см. рис. 3.8. За t = 3 T выходной сигнал достигает 95% от своего установившегося значения и переходный процесс принято считать законченным.
Таким образом, при реакции на единичное ступенчатое воздействие выходная координата стремится к установившемуся значению K по экспоненциальной зависимости – см. рис. 3.8. За t = 3 T выходной сигнал достигает 95% от своего установившегося значения и переходный процесс принято считать законченным. . (3.23)
. (3.23) (3.24)
(3.24) При изменении частоты w от 0 до µ конец вектора R (w) описывает полуокружность в первом квадранте комплексной плоскости – см. рис. 3.9.
При изменении частоты w от 0 до µ конец вектора R (w) описывает полуокружность в первом квадранте комплексной плоскости – см. рис. 3.9.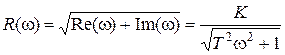 (3.25)
(3.25) . (3.26)
. (3.26) . (3.27)
. (3.27)



