
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристический полином замкнутой СУ. Алгебраические критерии устойчивостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В подразд. 1.4 вводится понятие устойчивых объектов и СУ с позиции их поведения. Показано, что устойчивость является необходимым условием функционирования СУ. В подразд. 2.3 понятие устойчивости связывается в решением ДУ, которое описывает поведение СУ. Там же сформулированы необходимое и достаточное условие устойчивости, а именно: для устойчивости СУ необходимо и достаточно, чтобы корни характеристического полинома принадлежали левой полуплоскости плоскости корней. Для СУ, построенных по принципу обратной связи, устойчивость определяет характеристический полином замкнутой СУ. Если модель типовой СУ задана структурной схемой (подразд. 2.5, рис. 2.2), то по ПФ звеньев прямого канала легко определяется оператор W Р(s) и структура СУ приводится к виду, изображенному на рис. 2.3. В подразд. 2.6 определяются ПФ по управлению и по ощибке замкнутой СУ через оператор W Р(s) разомкнутой системы. В обоих случаях ПФ замкнутой системы имеют одинаковый знаменатель – характеристический полином. С учетом обозначений W Р(s) = B Р(s) / A Р(s), характеристический полином A (s) замкнутой системы определяется выражением:
Таким образом, характеристический полином замкнутой системы равен сумме полиномов знаменателя и числителя ПФ разомкнутой системы. Принадлежность корней характеристического полинома левой части комплексной плоскости можно определить непосредственным вычислением корней. Также могут быть использованы критерии устойчивости. Алгебраические критерии устойчивости позволяют установить факт принадлежности корней полинома левой полуплоскости по соотношениям коэффициентов ai полинома Необходимым (но не достаточным) условием устойчивости является требование, чтобы все коэффициенты ai, i = 0,…, n, были одного знака (например, положительные). Если хотя бы один коэффициент полинома имеет противоположный знак относительно других коэффициентов, то это уже является достаточным условием принадлежности одного или нескольких корней правой полуплоскости. Для полинома первого порядка A 1(s)= a 1 s + a 0приведенное условие устойчивочти является не только необходимым, но и достаточным, так как единственный действительный корень s 1= - a 0/ a 1. Для полинома второго порядка A 2(s)= a 2 s 2+ a 1 s + a 0приведенное условие устойчивочти также является не только необходимым, но и достаточным, что следует из анализа формулы решения квадратного уравнения:
Для полиномов выше второго порядка это необходимое условие уже не является достаточным. Здесь ограничимся рассмотрением критерия устойчивости для полинома 3-го порядка – “ критерий Гурвица ”. Для полинома A 3(s) = a 3 s 3+ a 2 s 2+ a 1 s + a 0имеют место следующие соотношения, получаемые из сравнения произведений “средних” коэффициентов a 2 a 1и “крайних” коэффициентов a 3 a 0. При a 2 a 1> a 3 a 0 все три корня – левые (система устойчива); при a 2 a 1< a 3 a 0 пара комплексно-сопряженных корней – правые (система неустойчива); при a 2 a 1= a 3 a 0 пара сопряженных корней – чисто мнимые, то есть корни располагаются на оси мнимых (система находится на колебательной границе устойчивости). Проведем анализ устойчивости СУ, модель которой показана на рис. 4.1 (подразд. 4.1). В общем виде оператор W Р(s) записан в выражении (4.1) – см. подразд. 4.2. Приведем его к одной дробно-рациональной функции
Запишем теперь в общем виде характеристический полином замкнутой СУ
В результате имеем a 3= T 1 T 2, a 2= T 1 + T 2, a 1= 1, a 0= K. (7.5) Определим устойчивость этой СУ при K =10, T 1 = T 2= 1 с. При таких значениях параметров имеем a 2 a 1< a 3 a 0– система неустойчива. Проанализируем влияние на устойчивость рассматриваемой СУ усиления в контуре. Зафиксируем значения постоянных времени и будем варьировать параметр K. Из (7.5) видно, что этот параметр входит только в младший коэффициент характеристического полинома (a 0= K). При достаточном уменьшении коэффициента усиления неравенство a 2 a 1< a 3 a 0поменяет знак: a 2 a 1> a 3 a 0. Коэффициент усиления контура обратной связи, при котором система оказывается на границе устойчивости, называется критическим коэффициентом усиления. Для данной СУ, с учетом (7.5), получим
Для установленных параметров (T 1 = T 2= 1 с) получаем K кр= 2. Для всех K < K кримеем устойчивую СУ.
На рис. 7.1 изображены переходные процессы в рассматриваемой системе при различных коэффициентах усиления. Рис. 7.1 На рис. 7.1, а приведен процесс при K = 0.5 K кр= 1, на рис. 7.1, б приведен процесс при K = K кр= 2, и на рис. 7.1, в - процесс при K = 1.5 K кр= 3.
|
||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 1520; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.219.203 (0.01 с.) |

 . (7.1)
. (7.1)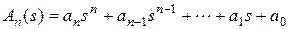 .
.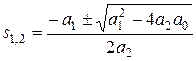 . (7.2)
. (7.2)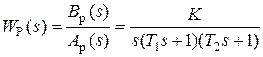 . (7.3)
. (7.3) (7.4)
(7.4) . (7.6)
. (7.6)



