
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нахождение характеристического уравнения замкнутой системыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Представим передаточную функцию разомкнутой системы в виде:
где В результате преобразований передаточной функции разомкнутой системы получаем:
Характеристическое уравнение замкнутой системы записывается как сумма числителя и знаменателя передаточной функции разомкнутой системы.
4. Выделение области устойчивости замкнутой системы в плоскости параметров Первое качество, по которому оценивают свойства системы автоматического управления (САУ), это ее устойчивость. Система устойчива, если с течением времени выходная величина системы будет стремиться к вынужденной составляющей ( При изменении какого–либо параметра системы может возникнуть неустойчивость, что влияет на качество регулирования системы, на конкурентоспособность. Поэтому значения коэффициента передачи и постоянной времени должны выбираться с точки зрения обеспечения устойчивости системы регулирования скорости. Весьма часто возникает необходимость исследовать влияние на устойчивость системы тех или иных ее параметров. Обычно рассматривают влияние таких параметров, которые могут быть изменены, например коэффициентов передачи и постоянных времени усилительно-преобразовательных элементов. Устойчивость – необходимое, но не достаточное условие работоспособности системы. Произведем исследование устойчивости системы в пространстве параметров D - разбиения. Интересующие нас параметры, tQ(s) + mP(s) – R(s) = 0, (4) где t – постоянная времени тахогенератора II; m – неизвестный коэффициент электромеханического преобразователя. Обозначим заданные неизвестные: Тогда уравнение (3) будет представлено в виде:
Приведем последнее выражение к виду (4):
Далее, воспользуемся критерием устойчивости Михайлова. Этот критерий основан на построении годографа Михайлова – кривой, которую описывает конец вектора D (j w)на комплексной плоскости при изменении w от 0 до ¥. Вектор D (j w)получается из характеристического уравнения замкнутой системы при подстановке s=jw, где
Формулировка критерия устойчивости Михайлова: Для устойчивости системы n -го порядка необходимо и достаточно, чтобы при изменении w от 0 до ¥ результирующий угол поворота вектора Михайлова Свойства годографа Михайлова говорят о том, что: ü если годограф Михайлова имеет плавную спиралевидную форму, последовательно обходит в положительном направлении (против часовой стрелки) n квадрантов, нигде не обращаясь в ноль и уходит в ¥ в n-м квадранте параллельно соответствующей оси, то система устойчива (рис. 3, а) ü если система находится на границе колебательной устойчивости, то годограф Михайлова проходит через начало координат (рис.3, б). ü
Рис. 3. Годографы Михайлова систем шестого порядка а) устойчивая система; б) система на границе колебательной устойчивости Ориентируясь на нахождение границы колебательной устойчивости с использованием частотного критерия устойчивости Михайлова, в предыдущем уравнении вместо оператора S подставляем S=jw и представляем вещественную и мнимую части характеристического уравнения в виде
где w – круговая частота гармонического входного сигнала. Эти два уравнения соответственно вещественная и мнимая части преобразованного характеристического уравнения. Решаем их относительно t и m с использованием определителей:
Где Подставляя численные значения известных параметров имеем:
Равенства (5) и (6) определяют τ и μ как функции от ω. Следовательно, при каждом значении ω=ωi можно вычислить значения τi и μi и нанести соответствующую точку на плоскость параметров τ и μ. Геометрическое место этих точек при изменении ω от -
Студент Obodnikova, 5/5 Порядок системы 5 Коэффициенты полиномов p1 p2 q1 q2 r1 r2 0 9.21E+0001 0.00E+0000 0.00E+0000 0.00E+0000 0.00E+0000 0.00E+0000 1 0.00E+0000 2.55E+0001 0.00E+0000 0.00E+0000 0.00E+0000 -1.00E+0000 2 -3.00E+0002 0.00E+0000 -1.00E+0000 0.00E+0000 1.15E+0000 0.00E+0000 3 0.00E+0000 -3.44E+0002 0.00E+0000 -1.15E+0000 0.00E+0000 4.95E-0002 4 1.49E+0001 0.00E+0000 4.95E-0002 0.00E+0000 -4.58E-0006 0.00E+0000 5 0.00E+0000 0.00E+0000 0.00E+0000 0.00E+0000 0.00E+0000 -1.98E-0007 Коэффициенты полиномов определителей степень D D1 D2 0 0.000000E+0000 0.000000E+0000 0.000000E+0000 1 0.000000E+0000 9.213750E+0001 0.000000E+0000 2 0.000000E+0000 0.000000E+0000 0.000000E+0000 3 7.998244E+0001 -2.753465E+0002 1.000000E+0000 4 0.000000E+0000 0.000000E+0000 0.000000E+0000 5 1.262992E+0000 -3.636064E+0002 1.212021E+0000 6 0.000000E+0000 0.000000E+0000 0.000000E+0000 7 5.179857E-0012 -7.336206E-0001 2.445402E-0003 8 0.000000E+0000 0.000000E+0000 0.000000E+0000 9 0.000000E+0000 2.940300E-0006 -9.801000E-0009 10 0.000000E+0000 0.000000E+0000 0.000000E+0000 Положительных корней в заданном диапазоне частот нет. W T M D -------------------------------------------------------- 1.0E-0004 1.151972E+0008 1.250274E-0002 7.998244E-0011 5.0E-0001 2.580717E-0002 1.623047E-0002 1.004331E+0001 1.0E+0000 -6.740548E+0000 2.725942E-0002 8.127006E+0001 1.5E+0000 -1.275395E+0001 4.515321E-0002 2.795888E+0002 2.0E+0000 -2.021082E+0001 6.923865E-0002 6.803813E+0002 2.5E+0000 -2.915433E+0001 9.867538E-0002 1.373239E+0003 3.0E+0000 -3.937832E+0001 1.325342E-0001 2.466700E+0003 3.5E+0000 -5.062444E+0001 1.698716E-0001 4.092983E+0003 4.0E+0000 -6.263411E+0001 2.097921E-0001 6.412726E+0003 4.5E+0000 -7.517098E+0001 2.514920E-0001 9.619721E+0003 5.0E+0000 -8.803172E+0001 2.942858E-0001 1.394565E+0004 5.5E+0000 -1.010503E+0002 3.376155E-0001 1.966483E+0004 6.0E+0000 -1.140977E+0002 3.810487E-0001 2.709892E+0004 6.5E+0000 -1.270791E+0002 4.242677E-0001 3.662170E+0004 7.0E+0000 -1.399292E+0002 4.670538E-0001 4.866378E+0004 7.5E+0000 -1.526074E+0002 5.092714E-0001 6.371734E+0004 8.0E+0000 -1.650930E+0002 5.508506E-0001 8.234087E+0004 8.5E+0000 -1.773804E+0002 5.917725E-0001 1.051639E+0005 9.0E+0000 -1.894754E+0002 6.320561E-0001 1.328917E+0005 9.5E+0000 -2.013919E+0002 6.717474E-0001 1.663102E+0005 1.0E+0001 -2.131494E+0002 7.109110E-0001 2.062904E+0005 2.6E+0002 -2.888831E+0004 9.629438E+0001 1.502018E+0012 5.1E+0002 6.125988E+0003 -2.041996E+0001 4.358713E+0013 7.6E+0002 4.408445E+0005 -1.469482E+0003 3.202710E+0014 1.0E+0003 1.829628E+0006 -6.098759E+0003 1.327506E+0015 1.3E+0003 4.945082E+0006 -1.648361E+0004 4.011195E+0015 1.5E+0003 1.077806E+0007 -3.592685E+0004 9.915207E+0015 1.8E+0003 2.053763E+0007 -6.845875E+0004 2.132940E+0016 2.0E+0003 3.565110E+0007 -1.188370E+0005 4.143765E+0016 2.3E+0003 5.776399E+0007 -1.925466E+0005 7.446592E+0016 2.5E+0003 8.874001E+0007 -2.958000E+0005 1.258302E+0017 2.8E+0003 1.306611E+0008 -4.355369E+0005 2.022849E+0017 3.0E+0003 1.858272E+0008 -6.194240E+0005 3.120703E+0017 3.3E+0003 2.567567E+0008 -8.558556E+0005 4.650615E+0017 3.5E+0003 3.461858E+0008 -1.153953E+0006 6.729156E+0017 3.8E+0003 4.570691E+0008 -1.523564E+0006 9.492207E+0017 4.0E+0003 5.925791E+0008 -1.975264E+0006 1.309643E+0018 4.3E+0003 7.561064E+0008 -2.520355E+0006 1.772077E+0018 4.5E+0003 9.512597E+0008 -3.170866E+0006 2.356791E+0018 4.8E+0003 1.181866E+0009 -3.939552E+0006 3.086577E+0018 5.0E+0003 1.451969E+0009 -4.839896E+0006 3.986899E+0018 5.3E+0003 1.765832E+0009 -5.886106E+0006 5.086040E+0018 5.5E+0003 2.127935E+0009 -7.093117E+0006 6.415253E+0018 5.8E+0003 2.542977E+0009 -8.476591E+0006 8.008905E+0018 6.0E+0003 3.015875E+0009 -1.005292E+0007 9.904630E+0018 6.3E+0003 3.551761E+0009 -1.183920E+0007 1.214347E+0019 6.5E+0003 4.155988E+0009 -1.385329E+0007 1.477005E+0019 6.8E+0003 4.834126E+0009 -1.611375E+0007 1.783267E+0019 7.0E+0003 5.591961E+0009 -1.863987E+0007 2.138351E+0019 7.3E+0003 6.435499E+0009 -2.145166E+0007 2.547876E+0019 7.5E+0003 7.370962E+0009 -2.456987E+0007 3.017876E+0019 7.8E+0003 8.404790E+0009 -2.801597E+0007 3.554816E+0019 8.0E+0003 9.543641E+0009 -3.181214E+0007 4.165605E+0019 8.3E+0003 1.079439E+0010 -3.598130E+0007 4.857613E+0019 8.5E+0003 1.216413E+0010 -4.054709E+0007 5.638686E+0019 8.8E+0003 1.366016E+0010 -4.553388E+0007 6.517159E+0019 9.0E+0003 1.529003E+0010 -5.096676E+0007 7.501872E+0019 9.3E+0003 1.706146E+0010 -5.687154E+0007 8.602184E+0019 9.5E+0003 1.898243E+0010 -6.327477E+0007 9.827991E+0019 9.8E+0003 2.106111E+0010 -7.020369E+0007 1.118974E+0020
По полученным значениям строим кривую D – разбиения в плоскости параметров τ и μ (рис. 4). Подставляя в характеристическое уравнение S = jw, мы подразумевали, что это соответствует границе колебательной устойчивости, т.е. при выборе параметров, значения которых лежат на это кривой, будут наблюдаться незатухающие колебания выходных величин. Чтобы выделить область устойчивости в плоскости t – m, штрихуют кривую Д–разбиения. Для этого на кривой указывают направление возрастания частоты w. При движении в этом направлении при D(w) > 0 кривая штрихуется двойной штриховкой слева, а при D(w) < 0 кривая штрихуется двойной штриховкой справа (см. рис.4).
Нахождение особых прямых При некоторой частоте w получаем
Приравнивая an к нулю, получаем:
Приравнивая свободный член характеристического уравнения a0 к нулю, получаем:
Таким образом, имеем только одну особую прямую
Рис. 4. Кривая D – разбиения в плоскости параметров τ и μ Из области подозрительной на устойчивость для дальнейшего рассмотрения выбираем точку с координатами:
|
|||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 702; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.50.1 (0.008 с.) |

 , (1)
, (1)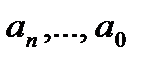 и bm…b0 - коэффициенты, выраженные через параметры (коэффициенты передач и постоянные времени) динамических звеньев исходной системы n > m.
и bm…b0 - коэффициенты, выраженные через параметры (коэффициенты передач и постоянные времени) динамических звеньев исходной системы n > m. (2)
(2) (3)
(3) (постоянная времени тахогенератора II),
(постоянная времени тахогенератора II),  (коэффициент электромеханического преобразователя) (Д–разбиение по двум параметрам)
(коэффициент электромеханического преобразователя) (Д–разбиение по двум параметрам) ), т.е. будет условно управляемый сигнал.
), т.е. будет условно управляемый сигнал. , входят в характеристическое уравнение линейно. Поэтому уравнение (3) может быть представлено в виде:
, входят в характеристическое уравнение линейно. Поэтому уравнение (3) может быть представлено в виде: ;
;  .
.

 , w - круговая частота гармонического выходного сигнала.
, w - круговая частота гармонического выходного сигнала. , где n -порядок дифференциального уравнения, которым описывается система управления.
, где n -порядок дифференциального уравнения, которым описывается система управления.

 ;
; ; (5)
; (5) , (6)
, (6)

 до +
до +  или
или  . Тогда система уравнений вырождается в одно уравнение особой прямой. Также эти особые прямые можно найти, приравняв коэффициент an к нулю (an = 0) и свободный член характеристического уравнения a0 (a0 = 0).
. Тогда система уравнений вырождается в одно уравнение особой прямой. Также эти особые прямые можно найти, приравняв коэффициент an к нулю (an = 0) и свободный член характеристического уравнения a0 (a0 = 0).
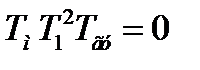 . Это выражение не содержит параметры τ и μ, а значит и не дает выражение для особой прямой.
. Это выражение не содержит параметры τ и μ, а значит и не дает выражение для особой прямой. Отсюда следует, что
Отсюда следует, что  .
.




