
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение лах, жлах, лфх разомкнутой системы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В соответствии с передаточной функцией разомкнутой системы ЛАХ имеет вид:
20lgKV = 20lg175=44,86; T1 = 0,25 (c); w1 = 3,57(c-1); T2 = 0,012 (c); w2 = 83,3(c-1); Tук = 0,024(c); wук = 42(c-1);
j(w) = - 90°- arctgwT1- arctgwT2 +
Для построения ЛФХ результаты расчётов сводим в таблицу Таблица 3.1 Результаты вычисления углов.
j(w) изобразим на рисунке 4.
Для построения ЛАХ некорректированной системы в соответствии с вышеприведенными аналитическими выражениями откладываем значение 20lgКV на w=1, через эту точку проводим прямую с наклоном –20дБ/декаду до первой наибольшей сопрягающей частоты w1=3,57 с-1 и далее в соответствии с выражением (3.36).
3.5 Определение устойчивости замкнутой системы.
Из всего многообразия способов, воспользуемся логарифмическим критерием устойчивости и корнями характеристического уравнения.
3.5.1 Определим устойчивость по логарифмическому критерию.
Замкнутая система будет неустойчива, если при j(wp) = - 180°, LН(wp)>0.
3.5.2 По корням характеристического уравнения замкнутой системы: С(р) = С4р4 + С3р3 + С2р2 + С1р + С0 =0
Корни этого уравнения определим с помощью ЭВМ и результат сведём в таблицу. Таблица 3.2 Корни системы
Т.к. корни р3 и р4 имеют положительную вещественную часть, то замкнутая система не устойчива.
Построение ЖЛАХ [LЖ(w)]
Методика синтеза. 1) По заданным значениям s и tрег, и графика h(w0t) выбираем подходящий переходный процесс, откуда получаем w0× t = 4,5 M=1,4. w0 = w0 откладываем на оси частот. Из w0 восстанавливаем отрезок прямой с наклоном – 40дБ/дек., до пересечения с LН(w) в точке w5. 2) Определение значения Т3:
w3 = 1/Т3 = 1,61; Откладываем w3 по оси частот, восстанавливаем из неё перпендикуляр до пересечения с отрезком прямой w0. Из полученной точки вправо проводим отрезок прямой с наклоном – 20дБ/дек. 3) Определить значение Т6 можно из соотношения:
w4 = 1/Т4 = 31,6 (с-1); С целью упрощения корректирующего устройства и улучшения качества и запаса устойчивости системы выбираем: w4 = 31,6 (с-1);
В точке пересечения LЖ(w) с наклоном – 20 дБ/дек. с LН(w) с наклоном -40 дБ/дек., после которой LЖ(w) совпадает с LН(w). При этом предварительно для увеличения w4 необходимо осуществить увеличение спрягающих частот wу и wк, что достигается с помощью охвата ЭМУ дополнительной жёсткой ООС. Для этого выходной сигнал ЭМУ подаётся на третью обмотку управления ЭМУ через рассчитанное дополнительное сопротивление обратной связи. Соотношения отражают нижепреведеные формулы:
Синтез корректирующих устройств. 4.1 Построение ЛАХ последовательного корректирующего звена. Осуществляем путем вычитания LПС(w)=LЖ(w)-LН(w) (4.1) По виду LПС(w) записываем его передаточную функцию и составляем принципиальную схему последовательного корректирующего устройства (рисунок 4.1). Передаточная функция последовательного корректирующего устройства:
T3=R1C1; T1=R2C2
Зададимся С1. С1 = 10 (мкФ)
R2×a = R1 + R2; Þ
4.2 Передаточную функцию параллельного корректирующего устройства получим через передаточную функцию последовательного корректирующего устройства и передаточную функцию звеньев, охваченных обратной связью.
Охватим ООС звенья, которые ухудшают устойчивость системы, т.е. двигатель и усилитель:
ВПС(р) = (1+ Т3р)(1+ Т1р); АПС(р) = (1+ Т6р)(1+ Т5р);
Выбираем тахогенератор ТГ – 2:

Рисунок 4.2 Т3 = (R1 + R5,6)×C1;
Зададимся С1:
Анализ динамики скорректированной системы.
5.1 Определение устойчивости замкнутой скорректированной системы по корням характеристического уравнения с помощью ЭВМ. Передаточная функция скорректированной системы в разомкнутом виде имеет вид:
Передаточная функция замкнутой скорректированной системы:
Корни характеристического уравнения ССК(р)=0 сведём в таблицу 5.1 Таблица 5.1
5.2 Построение кривой переходного процесса замкнутой скорректированной системы. Расчёт кривой замкнутой скорректированной системы ведём на ЭВМ, результаты приведены в приложении. Переходная функция изображена на рисунке 5.1 Показатели качества переходного процесса равны:
Nпер = 1; tрег = 1,5;
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 563; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.188.241 (0.007 с.) |

 (3.36)
(3.36)

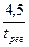 =
=  (c-1);
(c-1); (с);
(с); (с);
(с); Ä
Ä


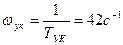 ;
; (4.2)
(4.2) ; (4.3)
; (4.3) ; (4.4)
; (4.4) (c);
(c); (4.5)
(4.5) ; (4.6)
; (4.6)

 ; (4.7)
; (4.7)
 Þ
Þ  ; (4.8)
; (4.8)
 (4.9)
(4.9)
 ; (4.10)
; (4.10) (4.11)
(4.11) ;
;

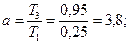
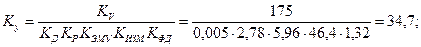



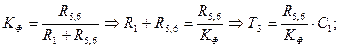


 (5.1)
(5.1)
 (5.2)
(5.2) %
%  =21%;
=21%;


