
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение топологической сортировки графа по топологическим сортировкам подграфов его разбиенияСодержание книги
Поиск на нашем сайте
Как правило, чем сложнее устроен граф, чем больше его размерность, тем труднее построить его топологическую сортировку, тем больше времени занимает процесс его предобработки. Предлагается алгоритм построения топологической сортировки графа алгоритма по сортировкам подграфов его разбиения; приводятся результаты вычислительного эксперимента, дающие возможность сравнить предлагаемый алгоритм с используемым ранее непосредственным построением топологической сортировки графа большой размерности [Воев]. Пусть граф Возникновение подобных ситуаций делает принципиально невозможным получение топологической сортировки графа Определение 1. Множество
называется множеством теряемых ребер графа
Во избежание потери ребер при разбиении графа
но пересечение этих подграфов не обязательно равно Ø. Например, для графа При построении сортировки произвольного графа Предлагаемый алгоритм содержит следующие основные этапы: — инициализуются значения корректировочных разностей для подграфов — последовательный просмотр топологической сортировки Пусть Если индекс то
иначе — переход на следующий этап; — последовательный просмотр топологической сортировки Пусть Если индекс то
иначе — М: если то
этап; если то если в пределах рассматриваемого топологического уровня
то вывести вершину с индексом граничных вершин данного топологического уровня; переход на метку М; иначе —
предыдущий этап.
Обобщение предложенного алгоритма на граф с большим числом подграфов не вызывает труда: для присвоения окончательного топологического номера каждой граничной вершине необходимо будет исследовать не два, а более подграфов, что потребует и большего общего количества арифметических операций. Таким образом, можно ожидать, что эффективность предложенного алгоритма будет зависеть от числа подграфов, а наибольший выигрыш во времени по сравнению с непосредственным построением топологической сортировки исходного графа, очевидно, будет наблюдаться, когда количество подграфов минимально (два, три), что и подтверждается результатами проведенного вычислительного эксперимента. В вычислительном эксперименте исследовалась эффективность с точки зрения временных затрат предложенного алгоритма построения топологической сортировки графа по топологическим сортировкам его подграфов по сравнению с непосредственным построением сортировки графа. Эксперимент проводился на графах различных по структуре последовательных алгоритмов. При этом изменялась размерность и количество подграфов, на которые разбивался граф. При проведении эксперимента фиксировалась размерность графа, начиная с которой новый алгоритм работал быстрее. Представлены примеры некоторых графов небольшой размерности (рис.10.4). Из полученных результатов вычислительного эксперимента, проведенного в среде MATLAB (табл.10.1), очевидно, что даже при сравнительно небольшом количестве вершин графа построение его топологической сортировки по топологическим сортировкам его подграфов происходит быстрее, чем непосредственное построение топологической сортировки всего графа. Это количество вершин фиксировалось, как только преимущество во времени достигало порядка
Рис.10.4. Примеры используемых графов При проведении вычислительного эксперимента отмечено, что эффективность построения топологической сортировки графа по топологическим сортировкам его подграфов в значительной степени зависит от способа его разбиения на подграфы. При разбиении следует стремиться к минимальному количеству теряемых ребер, а не равному количеству вершин в подграфах. Таблица 10.1 - Результаты вычислительного эксперимента
Предложенный алгоритм построения топологической сортировки графов позволяет проводить это построение на графах большой размерности быстрее, чем алгоритм, основывающийся на непосредственной обработке графа, поэтому исследование графов реальных последовательных алгоритмов, размерность которых, как правило, велика, с целью их распараллеливания имеет смысл проводить с помощью разработанного алгоритма.
Вопросы 1. Когда возникает семейство «похожих» алгоритмов? 2. Всегда ли можно точно построить граф алгоритма, содержащего условные операции? Почему? 3. Можно ли по имеющейся топологической сортировке графа получить топологические сортировки его подграфов? Как это сделать? Когда возникает такая необходимость? Привести пример. 4. Что назыв ется множеством теряемых ребер графа, когда это множество возникает? Привести примеры. 5. Какие вершины графа называются граничными вершинами? Привести примеры. 6. Написать программу, реализующую алгоритм построения топологической сортировки объединения двух графов по имеющимся топологическим сортировкам этих графов.
Литература 1. Воеводин В.В. Параллельные вычисления / В.В.Воеводин, Вл.В.Воеводин. — СПб.: БХВ-Петербург, 2002. — 608 с. 2. Харари Ф. Теория графов / Ф.Харари; пер.с англ. В.П.Козырева. — М.: Мир, 1973. — 300 с. 3. Уилсон Р. Введение в теорию графов / Р.Уилсон. — М.: Мир, 1977. — 207 с. 4. Кристофидес Н. Теория графов. Алгоритмический подход / Н.Кристофидес. — М.: Мир, 1978. — 432 с. 5. Новиков Ф.А. Дискретная математика для программистов / Ф.А.Новиков. — СПб.: Питер, 2006. — 364 с. 6. Иванов Б.Н. Дискретная математика. Алгоритмы и программы / Б.Н.Иванов. — М.: Лаборатория Базовых Знаний, 2001. — 288с. 7. Кобозева А.А., Нариманова Е.В. Метод построения топологической сортировки объединения графов, используемый при распараллеливании последовательных алгоритмов / Труды Одесского политехнического университета. – 2006. - №2(26). - С. 156-161.
Лекция 11. Использование операций гомоморфизма при построении топологических сортировок графов План
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 875; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.238.67 (0.009 с.) |

 является сложным для исследования и обработки в силу своей размерности или других причин, некоторые из которых уже указаны. Разложим граф на подграфы. Построим разбиение
является сложным для исследования и обработки в силу своей размерности или других причин, некоторые из которых уже указаны. Разложим граф на подграфы. Построим разбиение  множества вершин
множества вершин  :
:  Ø, для
Ø, для  .Каждое подмножество
.Каждое подмножество  , определяет порожденный подграф
, определяет порожденный подграф  графа
графа  . Для любого множества
. Для любого множества  порожденным подграфом называется максимальный подгаф графа
порожденным подграфом называется максимальный подгаф графа  . Построение сортировки графа
. Построение сортировки графа  , поскольку при выделении подграфов
, поскольку при выделении подграфов  (рис.1), т.к. объединение не содержит ребро
(рис.1), т.к. объединение не содержит ребро  , а значит при построении топологической сортировки графа
, а значит при построении топологической сортировки графа  ,
,  не учитывается возможность получения
не учитывается возможность получения 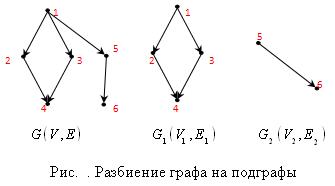 вершинами исходного графа с индексами 5 и 6 топологических номеров по цепочке 1, 5, 6.
вершинами исходного графа с индексами 5 и 6 топологических номеров по цепочке 1, 5, 6.
 множества
множества  Определение 2. Вершины графа
Определение 2. Вершины графа  на другой порожденный подграф
на другой порожденный подграф  , где множество
, где множество  содержит вершины, входящие в
содержит вершины, входящие в 

 . Построим сортировки наименьшей длины для каждого подграфа в отдельности, при этом каким-либо образом пометив граничные вершины. Без ограничения общности рассуждений, принимается, что запись каждого топологического уровня сортировки содержит сначала индексы всех вершин, не являющихся граничными, а если присутствуют граничные вершины, их индексы завершают запись. Такие топологические сортировки будут иметь минимальное количество уровней, равное длине критического пути подграфа плюс единица (следствие 2 утверждения 123).
. Построим сортировки наименьшей длины для каждого подграфа в отдельности, при этом каким-либо образом пометив граничные вершины. Без ограничения общности рассуждений, принимается, что запись каждого топологического уровня сортировки содержит сначала индексы всех вершин, не являющихся граничными, а если присутствуют граничные вершины, их индексы завершают запись. Такие топологические сортировки будут иметь минимальное количество уровней, равное длине критического пути подграфа плюс единица (следствие 2 утверждения 123). ,
,  , а
, а  — их топологические сортировки, представляющие массивы, в которых последовательно выписаны топологические уровни, начиная с первого. Обозначим
— их топологические сортировки, представляющие массивы, в которых последовательно выписаны топологические уровни, начиная с первого. Обозначим  ,
, 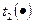 — топологические номера вершины в
— топологические номера вершины в  ,
,  соответственно,
соответственно,  — топологический номер граничной вершины в результирующей сортировке графа
— топологический номер граничной вершины в результирующей сортировке графа  , — корректировочные разности для
, — корректировочные разности для  . Корректировочной разностью подграфа
. Корректировочной разностью подграфа  и ее индексом в сортировке
и ее индексом в сортировке  ,
,  ;
; 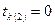 ;
;  ;
; — индекс очередной вершины в сортировке
— индекс очередной вершины в сортировке  =
=  , возврат в начало этапа;
, возврат в начало этапа;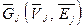 .
.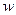 — индекс очередной вершины в сортировке
— индекс очередной вершины в сортировке  =
=  , возврат в начало этапа;
, возврат в начало этапа; ,
, ;обновление корректировочных разностей:
;обновление корректировочных разностей: ;
;  ; переход на предыдущий
; переход на предыдущий ,
, , что
, что  ,
,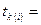 (
( )-
)- 
 ; переход на
; переход на с. С увеличением размерности графа преимущество возрастает. Например, для графа 1, количество вершин которого равно 250, а количество подграфов равно двум, время построения сортировки по предложенному алгоритму уже на 5 с меньше, чем при использовании алгоритма непосредственного построения топологической сортировки всего графа в целом. Кроме того, как следует из результатов эксперимента, чем больше количество подграфов разбиения графа, тем при большей его размерности достигается преимущество во времени по сравнению с построением топологической сортировки целого графа, как и предполагалось ранее.
с. С увеличением размерности графа преимущество возрастает. Например, для графа 1, количество вершин которого равно 250, а количество подграфов равно двум, время построения сортировки по предложенному алгоритму уже на 5 с меньше, чем при использовании алгоритма непосредственного построения топологической сортировки всего графа в целом. Кроме того, как следует из результатов эксперимента, чем больше количество подграфов разбиения графа, тем при большей его размерности достигается преимущество во времени по сравнению с построением топологической сортировки целого графа, как и предполагалось ранее.



