
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства временных разверток при фиксированном векторе задержекСодержание книги
Поиск на нашем сайте
Утверждение 3. При фиксированном векторе задержек множество временных разверток обладает следующими свойствами:
Пусть векторы
Следовательно
Следовательно Для любого
Т.е. вектор При фиксированном ненулевом векторе задержек Утверждение 4. Пусть Действительно:
Таким образом, конус обобщенных временных разверток Надо выяснить, когда множества Утверждение 5. Пусть СЛАУ
совместна и вектор Действительно, Совместимость (3) дает достаточное условие совпадения Какова бы ни была развертка Утверждение 6. Пусть множество Таким образом, координаты развертки
Вопросы 1. Сформулировать критерий того, что вектор 2. Как связана временная развертка для суммы векторов задержек с временными развертками слагаемых? Показать. 3. Как связана временная развертка для для вектора задержек 4. Показать, что множество 5. Показать, что множество 6. Свойства множества временных разверток при фиксированном векторе задержек. Доказать.
Литература 1. Воеводин В.В. Параллельные вычисления / В.В.Воеводин, Вл.В.Воеводин. — СПб.: БХВ-Петербург, 2002. — 608 с. 2. Харари Ф. Теория графов / Ф.Харари; пер.с англ. В.П.Козырева. — М.: Мир, 1973. — 300 с. 3. Уилсон Р. Введение в теорию графов / Р.Уилсон. — М.: Мир, 1977. — 207 с. 4. Кристофидес Н. Теория графов. Алгоритмический подход / Н.Кристофидес. — М.: Мир, 1978. — 432 с. 5. Новиков Ф.А. Дискретная математика для программистов / Ф.А.Новиков. — СПб.: Питер, 2006. — 364 с. 6. Иванов Б.Н. Дискретная математика. Алгоритмы и программы / Б.Н.Иванов. — М.: Лаборатория Базовых Знаний, 2001. — 288с.
Лекция 15. Векторные свойства временных разверток (продолжение) План
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 535; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.86.58 (0.005 с.) |

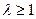 является временной разверткой;
является временной разверткой; ,
,  являются временными развертками для вектора задержек
являются временными развертками для вектора задержек 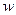 . Тогда:
. Тогда: -
- 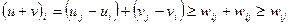 ,
, .
. ,
,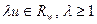 .
. имеем:
имеем: ,
, ,
, 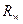 - выпукло.
- выпукло. . Несмотря на то, что множество
. Несмотря на то, что множество  - какая-нибудь фиксированная временная развертка из
- какая-нибудь фиксированная временная развертка из 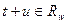 .
. -
-  ,
,  -
- 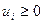 для всех подходящих пар
для всех подходящих пар  . Тогда
. Тогда -
- 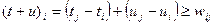 .
. -
-  (3)
(3) является ее решением. Тогда множества
является ее решением. Тогда множества 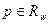 . Тогда в силу утверждения 4, множество
. Тогда в силу утверждения 4, множество 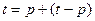 . Рассмотрим вектор
. Рассмотрим вектор  . Имеем
. Имеем  -
- 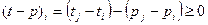 , т.е.
, т.е.  .
.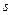 . Чем характерна временная развертка
. Чем характерна временная развертка 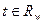 , она получается как сумма развертки из
, она получается как сумма развертки из  является обобщенной временной разверткой. Пусть дуга идет из
является обобщенной временной разверткой. Пусть дуга идет из  в
в  . Т.к.
. Т.к.  достигает в
достигает в 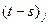 -
- 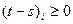 . Отсюда вытекает
. Отсюда вытекает 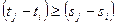 . Это означает, что имеет место
. Это означает, что имеет место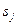 -
-  .
.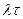 с временной разверткой для вектора задержек
с временной разверткой для вектора задержек  ? Показать.
? Показать.


