
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ориентированная задержка цикла. Уравновешенный циклСодержание книги
Поиск на нашем сайте
Задание вектора реализации Выясним, какие свойства графа алгоритма приводят к совместимости системы (3).
Пример. Пусть
2. Условие совпадения множеств Утверждение 7. СЛАУ (3) совместна тогда и только тогда, когда все циклы графа алгоритма уравновешены, или граф алгоритма не имеет циклов. Доказательство. Предположим, что СЛАУ (3)
На рис 15.2(б): дуге Пусть теперь граф алгоритма либо не имеет циклов, либо все его циклы уравновешены. Покажем, что СЛАУ (3) будет совместной. Не ограничивая общности будем считать граф алгоритма односвязным. Возьмем, например, первую вершину и припишем Пусть вторая вершина также принадлежит подграфу. В силу сделанного предположения об односвязности подграфа это означает, что добавленная дуга образует с некоторыми дугами подграфа какие-то циклы. Выберем любой из таких циклов и установим в нем направление обхода, при котором добавленая дуга проходится в положительном направлении. Пусть начальная вершина добавленной дуги иммет номер
Решение системы (3) в случае односвязности графа однозначно определяется при фиксации значения любой из его координат
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 541; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.252.215 (0.009 с.) |

 порождает некоторый вектор задержек
порождает некоторый вектор задержек  . В этом случае величину невязки
. В этом случае величину невязки  -
-  можно трактовать как время незапланированного простоя в процессе использования в качестве аргумента
можно трактовать как время незапланированного простоя в процессе использования в качестве аргумента  -ой операции результата, полученного
-ой операции результата, полученного  -ой операцией. Аналогичная трактовка имеет смысл и в случае произвольного вектора задержек
-ой операцией. Аналогичная трактовка имеет смысл и в случае произвольного вектора задержек 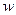 . Если какой-то результат не используется, то его надо где-то хранить, поэтому невязки
. Если какой-то результат не используется, то его надо где-то хранить, поэтому невязки  характеризуют времена дополнительного хранения данных, как входных, так и промежуточных, обусловленные взаимной «несогласованностью» развертки
характеризуют времена дополнительного хранения данных, как входных, так и промежуточных, обусловленные взаимной «несогласованностью» развертки  и вектора задержек
и вектора задержек 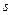 минимизирует каждое из таких времен.
минимизирует каждое из таких времен. Пусть задан вектор задержек
Пусть задан вектор задержек  -ая дуга проходится
-ая дуга проходится  раз в положительном направлении и
раз в положительном направлении и  раз в отрицательном. Сумму величин
раз в отрицательном. Сумму величин  по всем
по всем  , соответствующим дугам цикла, будем называть ориентированной задержкой цикла. Цикл, у которого ориентированная задержка равна 0, будем называть уравновешенным.
, соответствующим дугам цикла, будем называть ориентированной задержкой цикла. Цикл, у которого ориентированная задержка равна 0, будем называть уравновешенным. . На рис.15.1(а) дан пример уравновешенного цикла, а на рис. 15.1(б) – неуравновешенного.
. На рис.15.1(а) дан пример уравновешенного цикла, а на рис. 15.1(б) – неуравновешенного. и
и 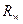 с точностью до параллельного переноса
с точностью до параллельного переноса -
- 
 совместна и вектор
совместна и вектор  задает ее решение. Выберем в графе алгоритма любой цикл, если он в нем имеется, и установим направление обхода. Каждому проходу
задает ее решение. Выберем в графе алгоритма любой цикл, если он в нем имеется, и установим направление обхода. Каждому проходу  -
-  . Просуммируем все равенства согласно обходу дуг цикла. В правой части суммы будет стоять ориентированная задержка цикла. Левая часть суммы будет равна нулю, т.е. цикл уравновешенный. Действительно, при каждом проходе соседних дуг цикла инцидентная им вершина учитывается дважды. Соответствующая этой вершине величина
. Просуммируем все равенства согласно обходу дуг цикла. В правой части суммы будет стоять ориентированная задержка цикла. Левая часть суммы будет равна нулю, т.е. цикл уравновешенный. Действительно, при каждом проходе соседних дуг цикла инцидентная им вершина учитывается дважды. Соответствующая этой вершине величина  :
:  -
-  . При сложении в левой части
. При сложении в левой части  :
:  . Но поскольку эта дуга обходится в отрицательном направлении, то ей ставится в соответствие
. Но поскольку эта дуга обходится в отрицательном направлении, то ей ставится в соответствие  . При сложении в левой части
. При сложении в левой части  какое-нибудь значение. Предположим, что построен односвязный подграф, и его вершинам приписаны такие значения
какое-нибудь значение. Предположим, что построен односвязный подграф, и его вершинам приписаны такие значения  , конечная – номер
, конечная – номер  . Соответствующие значения
. Соответствующие значения  и
и  определены раньше.Обойдем все дуги цикла, начиная с
определены раньше.Обойдем все дуги цикла, начиная с  . Сумма правых частей, принимая во внимание уравновешенность цикла, даст
. Сумма правых частей, принимая во внимание уравновешенность цикла, даст 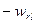 . Следовательно, уравнение (3) для
. Следовательно, уравнение (3) для  -ой дуги уже выполнено. Продолжая процесс присоединения новых дуг, припишем в конце концов всем вершинам графа алгоритма такие значения
-ой дуги уже выполнено. Продолжая процесс присоединения новых дуг, припишем в конце концов всем вершинам графа алгоритма такие значения 


