
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пространственно-временные развертки.Содержание книги
Поиск на нашем сайте До сих пор форма представления временных разверток не имела для нас существенного значения: допускалась произвольная нумерация вершин графовалгоритмов, временные развертки рассматривались как векторы. Это дало возможность выявить наиболее общие свойства.. Представление временных разверток в виде векторов соответствует такому описанию алгоритма, где множество выполняемых операций идентифицируется одним целочисленным параметром. Это в общем случае не очень удобно. Для повышения эффективности исследований необходимо более тесно связывать как граф алгоритма, так и формы представления временных разверток с формами записи алгоритмов. При практической реализации алгоритмов устанавливается по сути дела взаимно-однозначное соответствие между множеством вектор-индексов (параметрами циклов) и множеством операций, выполняемых в процессе реализации алгоритма. Это подсказывает естественный путь размещения вершин графа алгоритма. Будем отождествлять вершины с вектор-индексами и считать их точками конечномерных пространств. Тогда множество вершин будет заполнять некоторую область, которая может быть многосвязной и состоять из подобластей разной размерности. Напомним, что точки-вершины имеют целочисленные координаты, хотя это требование, вообще говоря, не обязательно. Теперь ясно, что и временые развертки нужно рассматривать как функции, заданные на множестве точек-вершин. Будем считать, что вершины графа алгоритма размещены в некоторой области Одна из основных задач исследования структуры алгоритма – изучение множества параллельных форм. Каждая параллельная форма определяет группы одновременно выполняемых операций, называемые ярусами. В целом любая параллельная форма определяет некоторое множество временных разверток. Если же развертки задавать функциями Исследование параллельных форм будет осуществляться тем эффективнее, чем проще устроено множество допустимых функций Предположим, что пространственно-временные развертки каким-то приемлемым образом продолжены на всю область Будем считать, что пространственно-временные развертки
Предположим, что граф алгоритма имеет хотя бы одну подходящую временную развертку. Она определяет систему поверхностей уровней. Эти поверхности могут быть односвязными (рис.15.3(а)), многосвязными (рис.15.3(б)). Здесь цифрами отмечены поверхности уровней, соответствующие последовательным значениям Системам поверхностей уровней одной пространственно-временной развертки определяет некоторую параллельную форму алгоритма.
Вопросы 1. Что характеризует время дополнительного хранения данных? 2. Что называется ориентированной задержкой цикла? 3. Какой цикл называется уравновешенным? 4. Сформулировать и доказать критерий совпадения множеств 5. Какие временные развертки называются пространственно-временными?
Литература 1. Воеводин В.В. Параллельные вычисления / В.В.Воеводин, Вл.В.Воеводин. — СПб.: БХВ-Петербург, 2002. — 608 с. 2. Харари Ф. Теория графов / Ф.Харари; пер.с англ. В.П.Козырева. — М.: Мир, 1973. — 300 с. 3. Уилсон Р. Введение в теорию графов / Р.Уилсон. — М.: Мир, 1977. — 207 с. 4. Кристофидес Н. Теория графов. Алгоритмический подход / Н.Кристофидес. — М.: Мир, 1978. — 432 с. 5. Новиков Ф.А. Дискретная математика для программистов / Ф.А.Новиков. — СПб.: Питер, 2006. — 364 с. 6. Иванов Б.Н. Дискретная математика. Алгоритмы и программы / Б.Н.Иванов. — М.: Лаборатория Базовых Знаний, 2001. — 288с.
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 672; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 . Если задана какая-то временная развертка, то тем самым каждой из точек вершин
. Если задана какая-то временная развертка, то тем самым каждой из точек вершин  приписывается вполне определенное число, совпадающее с времененм выполнения соответствующей операции. Таким образом, временные развертки – это функции
приписывается вполне определенное число, совпадающее с времененм выполнения соответствующей операции. Таким образом, временные развертки – это функции  , определенные на некотором дискретном множестве точек
, определенные на некотором дискретном множестве точек  . Пусть это множество содержит какие-то вершины графа алгоритма. Тогда соответствующие этим вершинам операции выполняются в один и тот же момент, т.е. образуют ярус параллельной формы. Различные ярусы задаются различными поверхностями уровня пространственно-временных разверток.
. Пусть это множество содержит какие-то вершины графа алгоритма. Тогда соответствующие этим вершинам операции выполняются в один и тот же момент, т.е. образуют ярус параллельной формы. Различные ярусы задаются различными поверхностями уровня пространственно-временных разверток.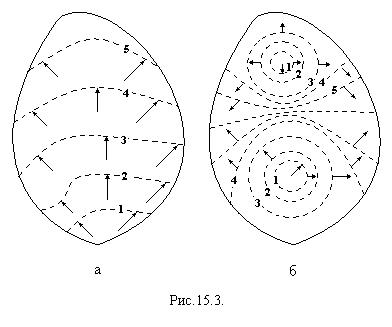 Пусть для простоты область
Пусть для простоты область  пространственно-временные развертки
пространственно-временные развертки  они меняются непрерывно, то по одну их сторону всегда будут находиться вершины, для которых выполнение соответствующих операций происходит до момента
они меняются непрерывно, то по одну их сторону всегда будут находиться вершины, для которых выполнение соответствующих операций происходит до момента  и
и 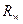 с точностью до параллельного переноса.
с точностью до параллельного переноса.


