
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства топологической сортировки графаСодержание книги
Поиск на нашем сайте
Утверждение 111 показывает, что вершины графа любого алгоритма можно разбить, по крайней мере, на три группы. Первая группа содержит не менее одной входной вершины, третья – не менее одной выходной вершины. Вторая группа – все остальные вершины. Соответствующие группы операций алгоритма могут быть выполнены последовательно друг за другом. Наибольший интерес с точки зрения анализа алгоритма вызывает вторая группа. Утверждение 123. Пусть задан ориентированный ациклический граф, имеющий Доказательство. Выберем в графе любое число входных вершин и пометим их индексом 1. Удалим из графа помеченные вершины и инцидентные им ребра. Оставшийся граф также ориентированный и ациклический. Выберем в нем любое число входных вершин (в соответствии с утверждением 111 хотя бы одна такая вершина есть) и пометим их индексом 2. Снова удалим помеченные вершины и инцидентные им ребра. Продолжим этот процесс, пока не исчерпаем весь граф. Так как при каждом помечивании помечается не менее одной вершины, то число различных индексов не превышает числа вершин. Следствие 1. Никакие две вершины с одинаковыми индексами не являются смежными. Следствие 2. Минимальное число индексов, которыми можно пометить все вершины графа, на 1 больше длины его критического пути. Следствие 3. Для любого натурального числа Разметка вершин графа, проведенная в соответствии с утверждением 123, называется топологической сортировкой, а вершины, помеченные одним индексом, образуют топологический уровень. Если при топологической сортировке графа некоторая вершина помечена индексом Пример. Построить топологическую сортировку графа
Рис.9.1. Исходный граф
Если на каждом шаге построения топологической сортировки помечать все возможные вершины, то количество уровней будет минимальным и равным 7 (рис.9.2) (сравнить с длиной критического пути графа, которая равна 6), при этом разбиение множества вершин графа на топологические уровни будет иметь следующий вид:
Таким образом, каждому графу может соответствовать множество различных топологических сортировок.
рис.9.2. Топологическая сортировка графа, содержащая минимальное количество уровней
Замечание 1000. Утверждение 123 остается в силе, если неравенство Обобщенная топологическая сортировка является удобным промежуточным объектом в процессе отыскания нужной топологической сортировки. Если найдена нетривиальная обобщенная топологическая сортировка, то для нахождения топологической сортировки не обязательно снова рассматривать весь граф. Довольно часто могут быть получены хорошие результаты, если отыскать подходящие топологические сортировки для подграфов, определяемых группами вершин обобщенной топологической сортировки, и из них составить топологическую сортировку исходного графа, используя предложенный ниже алгоритм построения топологической сортировки объединения графов Ниже обязательно привести пример. Топологическая сортировка называется линейной, если индексы любых вершин различны. В этом случае говорят, что граф линейно упорядочен. Если топологическая сортировка (или обощенная топологическая сортировка) не являются линейными, то из нее легко получить другие сортировки с бóльшим числом индексов.
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 894; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.143.150 (0.008 с.) |

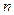 вершин. Существует натуральное число
вершин. Существует натуральное число 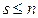 , для которого все вершины графа можно так пометить одним из индексов
, для которого все вершины графа можно так пометить одним из индексов 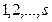 , что если дуга идет из вершины с индексом
, что если дуга идет из вершины с индексом 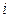 в вершину с индексом
в вершину с индексом  , то
, то  [Воев].
[Воев]. индексов.
индексов. , то длина всех путей, оканчивающихся в этой вершине, меньше
, то длина всех путей, оканчивающихся в этой вершине, меньше  (рис.9.1(а)). На рис.9.1(б-к) отражены последовательные шаги построения сортировки в соответствии с доказательством утверждения 123. В результате получено разбиение множества вершин графа на следующие топологические уровни:
(рис.9.1(а)). На рис.9.1(б-к) отражены последовательные шаги построения сортировки в соответствии с доказательством утверждения 123. В результате получено разбиение множества вершин графа на следующие топологические уровни: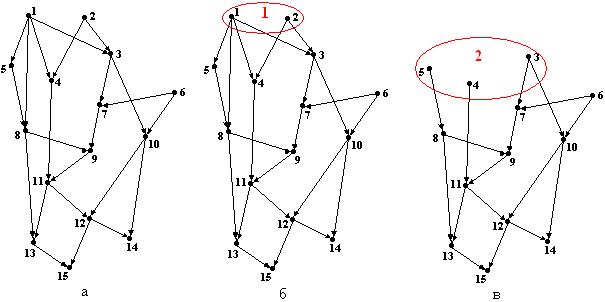



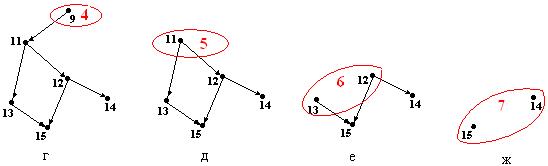
 , однако ни одно из следствий уже выполняться не будет. Такая разметка вершин графа называется обобщенной топологической сортировкой.
, однако ни одно из следствий уже выполняться не будет. Такая разметка вершин графа называется обобщенной топологической сортировкой.


