
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Влияние ошибок округления на алгоритмыСодержание книги
Поиск на нашем сайте Чтобы анализировать ошибки, порождаемые самим алгоритмом, требуется исследовать влияние погрешностей округлений в арифметических операциях. В такого рода исследованиях используется свойство, называемое обратной устойчивостью, определяемое следующим образом. Пусть
Величина Для погрешности вычисленного значения
являющаяся произведением абсолютного числа обусловленности При обратной устойчивости
Программирование численных алгоритмов Как правило, три главных соображения, которыми руководствуются при машинной реализации численных алгоритмов или выборе готовой программы, это · Простота использования, · Надежность, · Временные затраты. Если какая-то из уже существующих программ способна решить конкретную рассматриваемую задачу,то простота ее использования может перевесить все остальные факторы, например, временные затраты. Действительно, если задачу нужно решить лишь один или несколько раз, то, как правило, легче воспользоваться универсальной программой, составленной экспертами, чем писать свою более специализированную программу. Существует три основные формы использования программных продуктов, разработанных другими специалистами. Первая форма – это традиционная библиотека, представляющая собой набор программ для решения фиксированного круга задач, например, решения систем линейных уравнений, вычисления собственных значений и т.д. Примером может служить библиотека LAPACK. Второй формой являются программные среды, значительно «более дружественные к пользователю» по сравнению с библиотеками типа LAPACK. Это достигается ценой утраты производительности. Эту форму представляет коммерческая система Matlab и ряд подобных ей систем. Matlab можно рассматривать как простую интерактивную программную среду, где большинство операций линейной алгебры реализованы как встроенные функции. Однако Matlab принимает ряд алгоритмических решений автоматически, не консультируясь с пользователем, поэтому получаемые этим путем программы могут работать медленнее, чем удачно выбранные библиотечные программы. Третья форма – это шаблоны или, иначе говоря, рецепты для сборки сложных алгоритмов из более простых «строительных блоков». Шаблоны полезны в ситуации, когда алгоритм можно построить многими разными способами, но при этом отсутствует простое правило выбора наилучшей конструкции для конкретной входной задачи. Таким образом, значительная роль в конструировании оставлена пользователю. Примером подобного подхода может служить книга «Шаблоны для решения линейных систем. Строительные блоки для итерационных методов».
Вопросы
Литература
2. Кобозєва А.А., Мачалін І.О., Хорошко В.О. Аналіз захищеності інформаційних систем. - К.: Вид. ДУІКТ, 2010. – 316 с. 3. Кобозева А.А., Хорошко В.А. Анализ информационной безопасности. - К.: Изд.ГУИКТ, 2009. – 251 с. 4. Деммель Дж. Вычислительная линейная алгебра / Дж.Деммель; пер.с англ. Х.Д.Икрамова. — М.: Мир, 2001. — 430 с. 5. Бахвалов Н.С. Численные методы / Н.С.Бахвалов, Н.П.Жидков, Г.М.Кобельков. — М.: БИНОМ. Лаборатория знаний, 2006. — 636 с. 6. Каханер Д. Численные методы и программное обеспечение / Д.Каханер, К.Моулер, С.Нэш; пер. с англ. Х.Д.Икрамова. — М.: Мир, 2001. — 575 с. 7. E.Anderson, Z.Bai, C.Bischof, J.Demmel, J.Dongarra, J.Du Croz, A.Greenbaum, S.Hammarling, A.McKenney, S.Ostrouchov, and D.Sorensen. LAPACK Users’ Guide (2nd edition). SIAM, Philadelphia,PA, 1995.
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 911; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

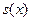 — некоторая вещественная функция. Через
— некоторая вещественная функция. Через  обозначим непосредственно выбранный численный алгоритм для вычисления
обозначим непосредственно выбранный численный алгоритм для вычисления  найдется малое
найдется малое  , такое, что:
, такое, что: .
. - это точный ответ для слабо возмущенной задачи
- это точный ответ для слабо возмущенной задачи  .
.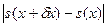 , исходя из соотношения (2.8), становится возможной оценка:
, исходя из соотношения (2.8), становится возможной оценка: ,
, и величины обратной ошибки
и величины обратной ошибки  .
.


