
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложность алгоритма по памятиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте В основном сложность алгоритмов обсуждается по времени, однако в некоторых случаях значимым является и вопрос используемой алгоритмом памяти. Этот вопрос был особенно актуальным на ранних этапах развития компьютеров при ограниченных объемах компьютерной памяти (как внутренней, так и внешней), однако не потерял своей актуальности и на сегодняшний день, поскольку с развитием информационных технологий, проникновением их во все сферы жизни общества, использование вычислительной техники для решения задач из разных областей человеческой деятельности, задач большой и очень большой размерности, этот анализ приобрел принципиальный характер. Все алгоритмы разделяются на такие, которым достаточно ограниченной памяти, и те, которым нужно дополнительное пространство [Макконнелл]. Иногда программистам приходится выбирать более медленный алгоритм лишь потому, что он обходится имеющейся памятью и не требует внешних устройств. Спрос на компьютерную память велик, поэтому и важен вопрос, какие данные необходимо хранить, а также эффективные способы хранения. Проиллюстрируем сказанное на примере. Предположим, что производится запись вещественного числа из сегмента [-10,10], имеющего один десятичный знак после запятой. При записи вещественного числа большинство компьютеров потратит от 4 до 8 байтов памяти. Однако если предварительно умножить число на 10, то для хранения полученного целого числа из сегмента [-100,100] потребуется всего 1 байт. При взгляде на программное обеспечение, предлагаекмое на рынке сегодня, ясно, что необходимый подробный анализ памяти во многих случаях проведен не был. Объем памяти, необходимый даже для сравнительно простых программ, измеряется мегабайтами. Разработчики программ часто не отдают себе отчет в необходимости экономии места, полагая, что если у пользователя недостаточно памяти, то он может ее приобрести и установить дополнительно. Этот подход является крайне неправильным и негативным, в результате его компьютеры приходят «в негодность» задолго до того, как они действительно устаревают. Новую струю внесло распространение в настоящий момент карманных компьютеров, у которых ограниченный объем памяти, что сделало критичным обеспечение возможности компактного хранения данных.
Вопросы 1. Какие основные характеристики алгоритма оцениваются при его анализе? 2. Как целесообразно оценивать «время» выполнения алгоритма? Почему? Что такое вычислительная сложность алгоритма? 3. В каких случаях сравнивается эффективность работы разных алгоритмов? 4. Должен ли анализ алгоритма учитывать особенности компьютера, на котором этот алгоритм реализован? Почему? 5. Влияют ли входные данные задачи на последовательность действий алгоритма? Привести пример. 6. Что представляют из себя классы входных данных? 7. Насколько значимым в настоящее время является вопрос используемой алгоритмом памяти? Литература 1. Дж. Макконнелл. Основы современных алгоритмов. 2-е дополненное издание. – М.: Техносфера, 2004. – 368 с. 2. Гуц А.К. Математическая логика и теория алгоритмов: Учебное пособие. – Омск: Изд-во Наследие. Диалог-Сибирь, 2003. – 108 с. 3. Деммель Дж. Вычислительная линейная алгебра / Дж.Деммель; пер.с англ. Х.Д.Икрамова. — М.: Мир, 2001. — 430 с. 4. Бахвалов Н.С. Численные методы / Н.С.Бахвалов, Н.П.Жидков, Г.М.Кобельков. — М.: БИНОМ. Лаборатория знаний, 2006. — 636 с. 5. Каханер Д. Численные методы и программное обеспечение / Д.Каханер, К.Моулер, С.Нэш; пер. с англ. Х.Д.Икрамова. — М.: Мир, 2001. — 575 с.
Лекция 4. Оценка вычислительной сложности алгоритма План Предварительные шаги для оценки вычислительной сложности алгоритма Скорость роста алгоритма Анализ подходов, связанных с поиском информации Предварительные шаги для оценки вычислительной сложности алгоритма Подсчет вычислительной сложности алгоритма состоит из двух основных шагов: Шаг 1. Выбор значимой операции или группы операций. Шаг 2. Определение, какие из выбранных операций содержатся в теле алгоритма, а какие составляют накладные расходы или уходят на регистрацию и учет данных. В качестве значимых часто (но не обязательно) выступают операции двух типов:
Арифметические операции разбиваются на две группы:
Аддитивные операторы (сложения) включают сложение, вычитание, увеличение и уменьшение счетчика. Мультипликативные операторы (умножения) включают умножение, деление, взятие остатка по модулю. Разбиение на эти две группы связано с тем, что умножения работают дольше, чем сложения. На практике некоторые алгоритмы считаются предпочтительнее других, если в них меньше умножений, даже если число сложений при этом пропорционально возрастает. Поскольку при анализе алгоритма выбор входных данных может существенно повлиять на его выполнение, желательно найти такие данные, которые обеспечивают как самое быстрое, так и самое медленное выполнение алгоритма, а также оценить среднюю эффективность алгоритма на всех возможных наборах данных. Очень часто при анализе алгоритма оценивается лишь наихудший (самый медленный) вариант.
Скорость роста алгоритма Точное значение количества операций, выполненных алгоритмом, не играет существенной роли в его анализе. Более важной оказывается скорость роста этого числа при возрастании объема входных данных. Она называется скоростью роста алгоритма. Именно эта характеристика часто и фигурирует как оценка вычислительной сложности алгоритма. Существенным является общий характер поведения алгоритмов, а не подробности этого поведения. Предположим, что количество операций четырех различных алгоритмов определяется в соответствии с функциями
где – Если рассмотреть графики этих функций (рис.4.1)
Рис. 4.1.
например, на промежутке от 1 до 35, то становится очевидным, что несмотря на то, что функция Таким образом, при анализе алгоритмов существенным является поведении функции зависимости количества операций от размера входных данных Некоторые часто встречающиеся функции приведены в таблице 4.1. Очевидно, что при небольших размерах входных данных значения функций отличаются незначительно, при росте этих размеров разница существенно возрастает. Поэтому существенным является поведение функции на больших объемах входных данных, поскольку на малых объемах принципиальная разница оказывается скрытой. Таблица 4.1-
Для иллюстрации последующего вывода рассмотрим пример функции, которая трактуется как закон зависимости количества арифметических операций некоторого гипотетического алгоритма от размера входных данных
Предложенная функция является суммой нескольких функций, скорость возрастания которых различна. Очевидно, что скорость роста всей Определение. Говорят, что функции
(читается: функция
Рассмотрим другой пример:
Ясно, что скорость возрастания
Из чего вытекает, что
Отбрасывая все младшие члены, скорость роста которых меньше, получаем порядок вычислительной сложности алгоритма [Макконнелл]. В предыдущем рассмотренном примере поскольку
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 3431; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |


 длина массива входных данных.
длина массива входных данных.
 сначала растет медленнее всех рассматриваемых функций, при росте аргумента она увеличивает скорость возрастания быстрее всех остальных, что приводит к тому, что, начиная с некоторого значения аргумента
сначала растет медленнее всех рассматриваемых функций, при росте аргумента она увеличивает скорость возрастания быстрее всех остальных, что приводит к тому, что, начиная с некоторого значения аргумента 
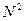


 .
. будет определяться самым быстровозрастающим слагаемым -
будет определяться самым быстровозрастающим слагаемым -  . Иначе говоря, быстрорастущие функции доминируют функции с более медленным ростом, что приводит к тому, что если сложность алгоритма представляет собой сумму двух или нескольких функций, то для оценки алгоритма целесообразно отбрасывать все функции, кроме тех, которые растут быстрее всех.
. Иначе говоря, быстрорастущие функции доминируют функции с более медленным ростом, что приводит к тому, что если сложность алгоритма представляет собой сумму двух или нескольких функций, то для оценки алгоритма целесообразно отбрасывать все функции, кроме тех, которые растут быстрее всех. и
и  связаны соотношением (или сравнимы)
связаны соотношением (или сравнимы)
 .
. .
. , остальными слагаемыми при оценке скорости роста можно пренебречь. Кроме того:
, остальными слагаемыми при оценке скорости роста можно пренебречь. Кроме того: ,
, .
. , то соответствующий гипотетический алгоритм имеет вычислительную сложность порядка
, то соответствующий гипотетический алгоритм имеет вычислительную сложность порядка 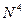 .
.


