Вопрос 14. Оценки временной сложности алгоритма.

Традиционно принято оценивать степень сложности алгоритма по объему используемых им основных ресурсов компьютера: процессорного времени и оперативной памяти. В связи с этим вводятся такие понятия, как временная сложность алгоритма и объемная сложность алгоритма.

Параметр временной сложности становится особенно важным для задач, предусматривающих интерактивный режим работы программы, или для задач управления в режиме реального времени. Часто программисту, составляющему программу управления каким-нибудь техническим устройством, приходится искать компромисс между точностью вычислений и временем работы программы. Как правило, повышение точности ведет к увеличению времени.

Объемная сложность программы становится критической, когда объем обрабатываемых данных оказывается на пределе объема оперативной памяти ЭВМ. На современных компьютерах острота этой проблемы снижается благодаря как росту объема ОЗУ, так и эффективному использованию многоуровневой системы запоминающих устройств. Программе оказывается доступной очень большая, практически неограниченная область памяти (виртуальная память). Недостаток основной памяти приводит лишь к некоторому замедлению работы из-за обменов с диском. Используются приемы, позволяющие минимизировать потери времени при таком обмене. Это использование кэш-памяти и аппаратного просмотра команд программы на требуемое число ходов вперед, что позволяет заблаговременно переносить с диска в основную память нужные значения. Исходя из сказанного можно заключить, что минимизация емкостной сложности не является первоочередной задачей. Поэтому в дальнейшем мы будем интересоваться в основном временной сложностью алгоритмов.

Время выполнения программы пропорционально числу исполняемых операций. Разумеется, в размерных единицах времени (секундах) оно зависит еще и от скорости работы процессора (тактовой частоты). Для того чтобы показатель временной сложности алгоритма был инвариантен относительно технических характеристик компьютера, его измеряют в относительных единицах. Обычно временная сложность оценивается числом выполняемых операций.

Как правило, временная сложность алгоритма зависит от исходных данных. Это может быть зависимость как от величины исходных данных, так и от их объема. Если обозначить значение параметра временной сложности алгоритма α символом Tα, а буквой V обозначить некоторый числовой параметр, характеризующий исходные данные, то временную сложность можно представить как функцию Tα(V). Выбор параметра V зависит от решаемой задачи или от вида используемого алгоритма для решения данной задачи.

Пример 1. Оценим временную сложность алгоритма вычисления факториала целого положительного числа.

Function Factorial(x:Integer): Integer;

Var m,i: Integer;

Begin m:=l;

For i:=2 To x Do m:=ro*i;

Factorial:=m

End;

Подсчитаем общее число операций, выполняемых программой при данном значении x. Один раз выполняется оператор m:=1; тело цикла (в котором две операции: умножение и присваивание) выполняется х — 1 раз; один раз выполняется присваивание Factorial:=m. Если каждую из операций принять за единицу сложности, то временная сложность всего алгоритма будет 1 + 2 (x — 1) + 1 = 2х Отсюда понятно, что в качестве параметра следует принять значение х. Функция временной сложности получилась следующей:

Tα(V)=2V.

В этом случае можно сказать, что временная сложность зависит линейно от параметра данных — величины аргумента функции факториал.

Пример 2. Вычисление скалярного произведения двух векторов А = (a1, a2, …, ak), В = (b1, b2, …, bk).

АВ:=0;

For i:=l To k Do AB:=AB+A[i]*B[i];

В этой задаче объем входных данных п = 2k. Количество выполняемых операций 1 + 3k = 1 + 3(n/2). Здесь можно взять V= k= п/2. Зависимости сложности алгоритма от значений элементов векторов А и В нет. Как и в предыдущем примере, здесь можно говорить о линейной зависимости временной сложности от параметра данных.

С параметром временной сложности алгоритма обычно связывают две теоретические проблемы. Первая состоит в поиске ответа на вопрос: до какого предела значения временной сложности можно дойти, совершенствуя алгоритм решения задачи? Этот предел зависит от самой задачи и, следовательно, является ее собственной характеристикой.

Вторая проблема связана с классификацией алгоритмов по временной сложности. Функция Tα(V) обычно растет с ростом V. Как быстро она растет? Существуют алгоритмы с линейной зависимостью Тα от V (как это было в рассмотренных нами примерах), с квадратичной зависимостью и с зависимостью более высоких степеней. Такие алгоритмы называются полиномиальными. А существуют алгоритмы, сложность которых растет быстрее любого полинома. Проблема, которую часто решают теоретики — исследователи алгоритмов, заключается в следующем вопросе: возможен ли для данной задачи полиномиальный алгоритм?

Функции, часто встречающиеся при анализе алгоритмов:

• log n (логарифмическое время),
• n (линейное время),
• n log n,
• n ² (квадратичное время),
• 2 ⁿ (экспоненциальное время).

Первые четыре функции имеют невысокую скорость роста и алгоритмы, время работы которых оценивается этими функциями, можно считать быстродействующими. Скорость роста экспоненциальной функции иногда характеризуют как «взрывную». Для сравнения допустим, что имеются алгоритмы, трудоемкость которых (число операций) достаточно точно отражается этими функциями. Пусть эти алгоритмы выполняются на компьютере, работающем со скоростью 10¹² операций в секунду. При длине входа n ≤ 100000 алгоритмы, скорость работы которых оценивается первыми четырьмя функциями, получат ответ за ничтожные доли секунды. Для алгоритма с трудоемкостью 2 ⁿ время работы оценивается следующим образом:

• n = 50 ≈ 19 минут,
• n = 60 ≈ 320 часов,
• n = 70 ≈ 37 лет.

 

Вопрос 15=49. Последовательные, циклические и рекурсивные алгоритмы.

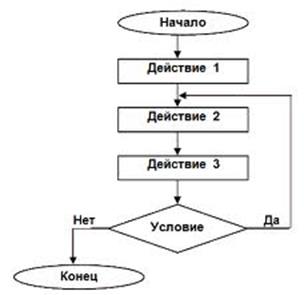
Последовательные алгоритмы – алгоритмы, в которых блоки выполняются последовательно друг за другом, в порядке заданной схемы.

 

Пример. Вычислить периметр треугольника со сторонами a,b,c.13

Алгоритм разветвляющейся структуры

На практике редко удается представить решение задачи в виде алгоритма

линейной структуры. Часто в зависимости от каких-либо промежуточных

результатов вычисления осуществляются либо по одним, либо по другим

формулам, т.е. в зависимости от выполнения некоторого логического условия

вычислительный процесс осуществляется по одной или другой формуле.

Алгоритм такого вычислительного процесса называется алгоритмом

разветвляющейся структуры.

Ветвление - управляющая структура, организующая выполнение лишь

одного из двух указанных действий в зависимости от справедливости

некоторого условия.

Условие - вопрос, имеющий два варианта ответа: да или нет.

Запись ветвления выполняется в двух формах: полной и неполной (Рис. 1 а, б).

а) полная форма б) неполная форма

 

Циклические алгоритмы – алгоритмы, в которых приходится многократно вычислять значения по одним и тем же математическим зависимостям (блок схемам) для различных значений входящих в них величин. Использование циклов позволяет существенно сократить объем схемы

алгоритма и длину соответствующей ей программы. Различают циклы с

заданным и неизвестным числом повторений. С заданным числом повторений -

цикл со счетчиком. С неизвестным числом повторений - цикл с предусловием,

цикл с постусловием.

 

Функция (или процедура), которая прямо или косвенно обращается к себе, называется рекурсивной. Рекурсия - метод определения функции через её предыдущие и ранее определенные значения, а так же способ

организации вычислений, при котором функция вызывает сама себя с другим аргументом

При реализации рекурсивных алгоритмов каждый шаг рекурсии не дает непосредственного решения задачи, но сводит ее к такой же задаче меньшего размера. Этот процесс должен приводить к задаче такого размера, когда

решение получается достаточно легко. Далее "обратный ход" дает последовательные решения для задачи все большего размера, вплоть до первоначального. В основе реализации процедуры с рекурсией лежит стек (память "магазинного" типа), где хранятся данные, участвующие во всех вызовах процедуры, при которых она еще не завершила свою работу. Рекурсия – это способ организации процесса вычисления, когда алгоритм обращается сам к себе. Принцип рекурсии позволяет решить сложную задачу путем последовательного решения более простых подзадач.Как правило, рекурсия необходима в тех случаях, когда требуется перебрать слишком много вариантов. Рекурсию принято считать как одну из разновидностей циклического алгоритма. Рекурсивная форма организации позволяет придать алгоритму более компактный вид. Таким образом, решается проблема от сложного к простому – содержание рекурсивного алгоритма отражает более сложный объект через более простой такого же типа. Обычно рекурсивный алгоритм содержит следующие основные части:

– условие для завершения цикла;

– тело рекурсии, которое включает действия, предназначенные для

выполнения на каждой итерации;

– шаг рекурсии, на котором рекурсивный алгоритм вызывает сам себя.

Различают прямую и косвенную рекурсию. В первом случае алгоритм

содержит функцию, которая сама себя вызывает. Если функция вызывает другую функцию, которая, в свою очередь, вызывает первую, то такая функция

называется косвенно рекурсивной.

Основное требование к рекурсивным алгоритмам – процесс обращения не

должен быть бесконечным. Другими словами, должна быть реализована

проверка завершения вызова, или в рекурсивном определении должно

присутствовать ограничение, при котором дальнейшая инициализация

рекурсии прекращается.

Примером рекурсивной функции является вычисление факториала числа.

 

int factoria(int n)

{

if (n) return n* factoria(n-1);

else return 1;

}

 

 

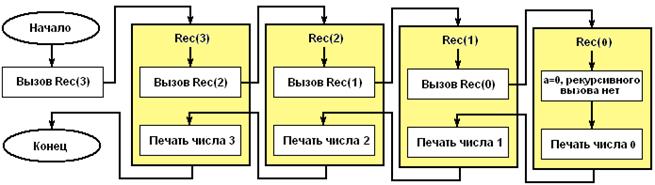
Пример рекурсивной процедуры:

procedure Rec(a: integer); begin if a>0 then Rec(a-1); writeln(a); end;

 

Рассмотрим, что произойдет, если в основной программе поставить вызов, например, вида Rec(3). Ниже представлена блок-схема, показывающая последовательность выполнения операторов.