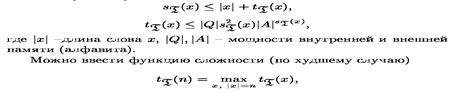Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Возникновение теории алгоритмовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Количественно-зависимые по трудоемкости алгоритмы Это алгоритмы, функция трудоемкости которых зависит только от размерности конкретного входа, и не зависит от конкретных значений:
Примерами алгоритмов с количественно-зависимой функцией трудоемкости могут служить алгоритмы для стандартных операций с массивами и матрицами – умножение матриц, умножение матрицы на вектор и т.д. Параметрически-зависимые по трудоемкости алгоритмы Это алгоритмы, трудоемкость которых определяется не размерностью входа (как правило, для этой группы размерность входа обычно фиксирована), а конкретными значениями обрабатываемых слов памяти:
Примерами алгоритмов с параметрически-зависимой трудоемкостью являются алгоритмы вычисления стандартных функций с заданной точностью путем вычисления соответствующих степенных рядов. Очевидно, что такие алгоритмы, имея на входе два числовых значения – аргумент функции и точность выполняют существенно зависящее от значений количество операций. а) Вычисление б) Вычисление Количественно-параметрические по трудоемкости алгоритмы Однако в большинстве практических случаев функция трудоемкости зависит как от количества данных на входе, так и от значений входных данных, в этом случае:
В качестве примера можно привести алгоритмы численных методов, в которых параметрически-зависимый внешний цикл по точности включает в себя количественно-зависимый фрагмент по размерности. Порядково-зависимые по трудоемкости алгоритмы Среди разнообразия параметрически-зависимых алгоритмов выделим еще оду группу, для которой количество операций зависит от порядка расположения исходных объектов. Пусть множество D состоит из элементов ( Определим Если Примерами таких алгоритмов могут служить ряд алгоритмов сортировки, алгоритмы поиска минимума и максимума в массиве. Рассмотрим более подробно алгоритм поиска максимума в массиве S, содержащим n элементов:
7. Асимптотический анализ функций. При анализе поведения функции трудоемкости алгоритма часто используют принятые в математике асимптотические обозначения, позволяющие показать скорость роста функции, маскируя при этом конкретные коэффициенты. Такая оценка функции трудоемкости алгоритма называетсясложностью алгоритмаи позволяет определить предпочтения в использовании того или иного алгоритма для больших значений размерности исходных данных.В асимптотическом анализе приняты следующие обозначения: 1. Оценка Пусть f(n) и g(n) – положительные функции положительного аргумента, n >= 1 (количество объектов на входе и количество операций – положительные числа), тогда:
Операция примитивной рекурсии частичных функций. Оператор примитивной рекурсии Rn позволяет определить (n+1) - местную функцию f по двум заданным функциям, одна из которых является n- местной функцией g, а другая (n+2) - местной функцией h. Функция f(x1, x2,..., xn, y) получается оператором примитивной рекурсии из функций g(x1, x2,..., xn) и функции h(x1, x2,..., xn, y, z), если: f(x1, x2,..., xn), 0) = g(x1, x2,..., xn)); (2) f((x1, x2,..., xn+1) = h(x1, x2,..., xn, y, f(x1, x2,..., xn, y)). Приведенная пара равенств (2) называется схемой примитивной рекурсии. Для понимания операции примитивной рекурсии необходимо заметить, что всякую функцию от меньшего числа аргументов можно рассматривать как функцию от большего числа аргументов. Существенным в операторе примитивной рекурсии является то, что независимо от числа переменных в f рекурсия ведется только по одной переменной у. Остальные n переменных x1, x2,..., xn на момент применения схемы (2) зафиксированы и играют роль параметров. Операция минимизации арифметических функций.
Сложностные классы задач.
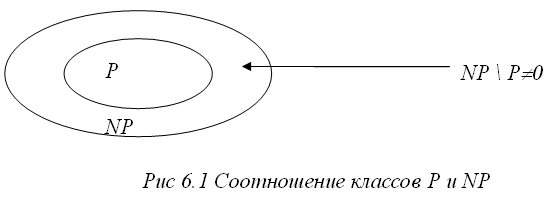
В начале 1960-х годов, в связи с началом широкого использования вычислительной техники для решения практических задач, возник вопрос о границах практической применимости данного алгоритма решения задачи в смысле ограничений на ее размерность. Какие задачи могут быть решены на ЭВМ за реальное время? Ответ на этот вопрос был дан в работах Кобмена (Alan Cobham, 1964), и Эдмнодса (Jack Edmonds, 1965), где были введены сложностные классы задач. 1) Класс P (задачи с полиномиальной сложностью) Задача называется полиномиальной, т.е. относится к классу P, если существует константа k и алгоритм, решающий задачу с Задачи класса P – это интуитивно, задачи, решаемые за реальное время. Отметим следующие преимущества алгоритмов из этого класса: o для большинства задач из класса P константа k меньше 6; o класс P инвариантен по модели вычислений (для широкого класса моделей); o класс P обладает свойством естественной замкнутости (сумма или произведение полиномов есть полином). Таким образом, задачи класса P есть уточнение определения «практически разрешимой» задачи. 2) Класс NP (полиномиально проверяемые задачи) Представим себе, что некоторый алгоритм получает решение некоторой задачи – соответствует ли полученный ответ поставленной задаче, и насколько быстро мы можем проверить его правильность? Рассмотрим, например задачу о сумме: Дано N чисел – А = (a1,…an) и число V. Задача: Найти вектор (массив) X=(x1,…,xn), xiє{0,1}, такой, что Содержательно: может ли быть представлено число V в виде суммы каких-либо элементов массива А. Если какой-то алгоритм выдает результат – массив X, то проверка правильности этого результата может быть выполнена с полиномиальной сложно-стью: проверка Формально: Содержательно задача относится к классу NP, если ее решение некоторым алгоритмом может быть быстро (полиномиально) проверено.
Примеры NP – полных задач 1 Задача о выполнимости схемы Рассмотрим схему из функциональных элементов «и», «или», «не» с n битовыми входами и одним выходом, состоящую не более, чем из O(
Будем понимать под выполняющим набором значений из множества {0,1} на входе схемы, такой набор входов – значения x1,…,xn, при котором на выходе схемы будет значение «1». Формулировка задачи – существует ли для данной схемы выполняющий набор значений входа. Очевидно, что задача принадлежит классу NP – проверка предъявленного выполняющего набора не сложнее количества функциональных элементов, и следовательно не больше чем O( Это была одна из первых задач, для которой была доказана ее NP полнота, т.е. любая задача из класса NP полиномиально сводима к задаче о выполнимости схемы. Решение этой задачи может быть получено перебором всех 2 Задача о сумме Уже рассмотренная задача о сумме также является NP–полной, отметим, что если количество слагаемых фиксировано, то сложность задачи является полиномиальной, так как: o для 2-х слагаемых o для 3-х слагаемых Однако в общем случае придется перебирать 3 Задача о клике Пусть дан граф G = G(V,E), где V – множество из n вершин, а E – множество ребер. Будем понимать под кликой максимальный по количеству вершин полный подграф в графе в G. Задача состоит в определении клики в заданном графе G Поскольку в полном графе на m вершинах имеется m(m-1)/2 ребер, то проверка, является ли данный граф полным, имеет сложность O (
Однако в общем случае придется проверять все подграфы с количеством вершин m = (2, n) на их полноту и определить максимальное значения m для которого в данном графе G существует полный подграф, что приводит к оценке в худшем случае:
Временная сложность.
Тогда:
Возникновение теории алгоритмов Развитие теории алгоритмов начинается с доказательства К. Гёделем теорем о неполноте формальных систем, включающих арифметику, первая из которых была доказана в 1931. Возникшее в связи с этими теоремами предположение о невозможности алгоритмического разрешения многих математических проблем вызвало необходимость стандартизации понятия алгоритма. Первые стандартизованные варианты этого понятия были разработаны в 30-х годах XX века в работах А. Тьюринга, А. Чёрча и Э. Поста. Предложенные ими машина Тьюринга, машина Поста и лямбда-исчисление Чёрча оказались эквивалентными друг другу. Основываясь на работах Гёделя, С. Клини ввел понятие рекурсивной функции, также оказавшееся эквивалентным вышеперечисленным. Одним из наиболее удачных стандартизованных вариантов алгоритма является введённое А.А.Марковым понятие нормального алгоритма. Оно было разработано десятью годами позже работ Тьюринга, Поста, Чёрча и Клини в связи с доказательством алгоритмической неразрешимости ряда алгебраических проблем. Следует отметить также немалый вклад в теорию алгоритмов, сделанный Д. Кнутом, A. Ахо и Дж. Ульманом. Одной из лучших работ на эту тему является книга «Алгоритмы: построение и анализ» Томаса Х. Кормена, Чарльза И. Лейзерсона, Рональда Л. Ривеста, Клиффорда Штайна. Алан Тьюринг высказал предположение (известное как Тезис Чёрча - Тьюринга), что любой алгоритм в интуитивном смысле этого слова может быть представлен эквивалентной машиной Тьюринга. Уточнение представления о вычислимости на основе понятия машины Тьюринга (и других эквивалентных ей понятий) открыло возможности для строгого доказательства алгоритмической неразрешимости различных массовых проблем (то есть проблем о нахождении единого метода решения некоторого класса задач, условия которых могут варьироваться в известных пределах). Простейшим примером алгоритмически неразрешимой массовой проблемы является так называемая проблема применимости алгоритма (называемая также проблемой остановки). Она состоит в следующем: требуется найти общий метод, который позволял бы для произвольной машины Тьюринга (заданной посредством своей программы) и произвольного начального состояния ленты этой машины определить, завершится ли работа машины за конечное число шагов, или же будет продолжаться неограниченно долго. В течение первого десятилетия истории теории алгоритмов неразрешимые массовые проблемы были обнаружены лишь внутри самой этой теории, а также внутри математической логики. Поэтому считалось, что теория алгоритмов представляет собой обочину математики, не имеющую значения для таких её классических разделов, как алгебра или анализ. Положение изменилось после того, как А.А. Марков и Э.Л.Пост в 1947 установили алгоритмическую неразрешимость известной в алгебре проблемы равенства для конечнопорождённых и конечноопределённых полугрупп. Впоследствии была установлена алгоритмическая неразрешимость и многих других «чисто математических» массовых проблем. В настоящее время теория алгоритмов развивается, главным образом, по трем направлениям. Классическая теория алгоритмов изучает проблемы формулировки задач в терминах формальных языков, вводит понятие задачи разрешения, проводит классификацию задач по классам сложности и др. Теория асимптотического анализа алгоритмов рассматривает методы получения асимптотических оценок ресурсоемкости или времени выполнения алгоритмов, в частности, для рекурсивных алгоритмов. Асимптотический анализ позволяет оценить рост потребности алгоритма в ресурсах (например, времени выполнения) с увеличением объема входных данных. Теория практического анализа вычислительных алгоритмов решает задачи получения явных функции трудоёмкости, интервального анализа функций, поиска практических критериев качества алгоритмов, разработки методики выбора рациональных алгоритмов. 3. Основные определения. Интуитивное определение алгоритма не позволяет рассматривать свойства алгоритмов как свойства формальных объектов. Поэтому математическое определение алгоритма необходимо по следующим причинам: 1) только при наличии формального определения алгоритма можно сделать вывод о разрешимости или неразрешимости каких-либо проблем; 2) это дает возможность для сравнения алгоритмов, предназначенных для решения одинаковых задач; 3) это дает возможность для сравнения различных проблем по сложности алгоритмов их решения. Одна из причин расплывчатости интуитивного определения алгоритма состоит в том, что объектом алгоритма может оказаться все, что угодно. Поэтому естественно было начать с формализации понятия объекта. В вычислительных алгоритмах объектами работы являются числа, в алгоритме шахматной игры - фигуры и позиции, при алгоритмизации производственных процессов объектами служат, например, показания приборов. Однако алгоритмы оперируют не с объектами реального мира, а с изображениями этих объектов. Поэтому алгоритмами в современной математике принято называть конструктивно задаваемые соответствия между изображениями объектов в абстрактных алфавитах. Абстрактным алфавитом называется любая конечная совокупность объектов, называемых буквами или символами данного алфавита. При этом природа этих объектов нас совершенно не интересует. Символом абстрактных алфавитов можно считать буквы алфавита какого-либо языка, цифры, любые значки и даже слова некоторого конкретного языка. Основным требованием к алфавиту является его конечность. Таким образом, можно утверждать, что алфавит - это конечное множество различных символов. Алфавит, как любое множество, задается перечислением его элементов. Итак, объекты реального мира можно изображать словами в различных алфавитах. Это позволяет считать, что объектами работы алгоритмов могут быть только слова. Тогда можно сформулировать следующее определение. Алгоритм есть четкая конечная система правил для преобразования слов из некоторого алфавита в слова из этого же алфавита. Слово, к которому применяется алгоритм, называется входным. Слово, вырабатываемое в результате применения алгоритма, называется выходным. Совокупность слов, к которым применим данный алгоритм, называется областью применимости этого алгоритма. Формальные определения алгоритма появились в 30-х - 40-х годах XX века. Можно выделить три основных типа универсальных алгоритмических моделей, различающихся исходными эвристическими соображениями относительно того, что такое алгоритм. Первый тип связывает понятие алгоритма с наиболее традиционными понятиями математики - вычислениями и числовыми функциями. Наиболее развитая и изученная модель этого типа - рекурсивные функции - является исторически первой формализацией понятия алгоритма. Эта модель основана на функциональном подходе и рассматривает понятие алгоритма с точки зрения того, что можно вычислить с его помощью. Второй тип основан на представлении алгоритма как некоторого детерминированного устройства, способного выполнять в каждый отдельный момент некоторые примитивные операции, или инструкции. Такое представление не оставляет сомнений в однозначности алгоритма и элементарности его шагов. Основной теоретической моделью этого типа, созданной в 30-х годах, является машина Тьюринга, которая представляет собой автоматную модель, в основе которой лежит анализ процесса выполнения алгоритма как совокупности набора инструкций. Третий тип алгоритмических моделей - это преобразования слов в произвольных алфавитах, в которых элементарными операциями являются подстановки, т.е. замены части слова (подслова) другим словом. Преимущество этого типа состоит в его максимальной абстрактности и возможности применить понятие алгоритма к объектам произвольной природы. Модели второго и третьего типа довольно близки и отличаются в основном эвристическими подходами. Примерами моделей этого типа являются нормальные алгоритмы Маркова и канонические системы Поста.
4. Сравнительные оценки алгоритмов. !!!После вопросов, отдельный лист!!! 5. Система обозначений в анализе алгоритмов. 6. Классификация алгоритмов по виду функции трудоёмкости. В зависимости от влияния исходных данных на функцию трудоемкости алгоритма может быть предложена следующая классификация, имеющая практическое значение для анализа алгоритмов:
|
||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 989; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.243.86 (0.01 с.) |

 (D) =
(D) = 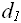 ,…,
,…, 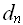 ) =
) = 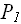 ,…,
,…, 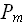 ), m =< n
), m =< n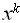 последовательным умножением
последовательным умножением 
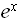 =
= 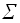 (
( /n!), с точностью до
/n!), с точностью до 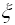
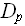 = {(
= {(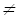
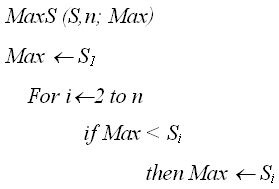
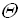 (тетта)
(тетта)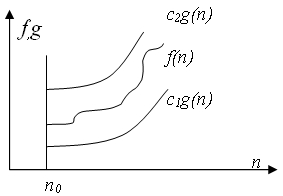


 ), где n - длина входа алгоритма в битах n = |D| [6].
), где n - длина входа алгоритма в битах n = |D| [6]. Dє
Dє 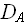 , |D|=n поставим в соответствие сертификат Sє
, |D|=n поставим в соответствие сертификат Sє 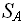 , такой что |S|=O (
, такой что |S|=O (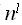 ) и алгоритм
) и алгоритм 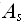 =
=  ).
).
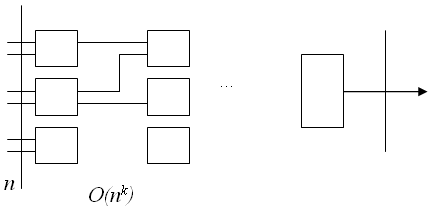
 Для этой, как и для всех других NP–полных задач не известен полиномиальный алгоритм решения.
Для этой, как и для всех других NP–полных задач не известен полиномиальный алгоритм решения.
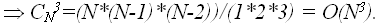
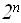 различных вариантов, так как по биномиальной теореме
различных вариантов, так как по биномиальной теореме 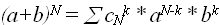 , а при a=b=1, имеем:
, а при a=b=1, имеем: 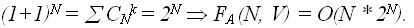
 ). Очевидно, что если мы рассматриваем подграф с m вершинами в графе G с вершинами (m < n), то всего существует
). Очевидно, что если мы рассматриваем подграф с m вершинами в графе G с вершинами (m < n), то всего существует 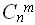 различных подграфов. Если в задаче о клике количество вершин клики фиксировано, то перебирающий алгоритм имеет полиномиальную сложность:
различных подграфов. Если в задаче о клике количество вершин клики фиксировано, то перебирающий алгоритм имеет полиномиальную сложность:

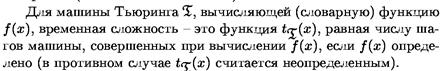 Время решения индивидуальной задачи зависит от скорости вычислителя, языка программирования и многого другого. Определяя качество алгоритма имеет смысл не учитывать эти факторы. Вместо времени мы будем оценивать количество характерных операций, которое необходимо выполнить, решая индивидуальную задачу данным алгоритмом.
Время решения индивидуальной задачи зависит от скорости вычислителя, языка программирования и многого другого. Определяя качество алгоритма имеет смысл не учитывать эти факторы. Вместо времени мы будем оценивать количество характерных операций, которое необходимо выполнить, решая индивидуальную задачу данным алгоритмом.