
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Класс NPC (NP – полные задачи)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Понятие NP – полноты было введено независимо Куком (Stephen Cook, 1971) и Левиным (журнал «Проблемы передачи информации», 1973,т.9, вып. 3) и основывается на понятии сводимости одной задачи к другой. Сводимость может быть представлена следующим образом: если мы имеем задачу 1 и решающий эту задачу алгоритм, выдающий правильный ответ для всех конкретных проблем, составляющих задачу, а для задачи 2 алгоритм решения неизвестен, то если мы можем переформулировать (свести) задачу 2 в терминах задачи 1, то мы решаем задачу 2. Таким образом, если задача 1 задана множеством конкретных проблем Если при этом Принято говорить, что задача задается некоторым языком, тогда если задача 1 задана языком L1, а задача 2 – языком L2, то полиномиальная сводимость обозначается следующим образом: L2 =< pL1. Определение класса NPC (NP-complete) или класса NP-полных задач требует выполнения следующих двух условий: во-первых, задача должна принадлежать классу NP (L є NP), и, во-вторых, к ней полиномиально должны сводиться все задачи из класса NP (Lx=< pL, для каждого Lx є NP), что схематично представлено на рис 6.2.
Для класса NPC доказана следующая теорема: Если существует задача, принадлежащая классу NPC, для которой существует полиномиальный алгоритм решения (F = O( Схема доказательства состоит в сведении любой задачи из NP к данной задаче из класса NPC с полиномиальной трудоемкостью и решении этой задачи за полиномиальное время (по условию теоремы). В настоящее время доказано существование сотен NP–полных задач, но ни для одной из них пока не удалось найти полиномиального алгоритма решения. В настоящее время исследователи предполагают следующее соотношение классов, показанное на рис 6.3 – P
Примеры NP – полных задач 1 Задача о выполнимости схемы Рассмотрим схему из функциональных элементов «и», «или», «не» с n битовыми входами и одним выходом, состоящую не более, чем из O(
Будем понимать под выполняющим набором значений из множества {0,1} на входе схемы, такой набор входов – значения x1,…,xn, при котором на выходе схемы будет значение «1». Формулировка задачи – существует ли для данной схемы выполняющий набор значений входа. Очевидно, что задача принадлежит классу NP – проверка предъявленного выполняющего набора не сложнее количества функциональных элементов, и следовательно не больше чем O( Это была одна из первых задач, для которой была доказана ее NP полнота, т.е. любая задача из класса NP полиномиально сводима к задаче о выполнимости схемы. Решение этой задачи может быть получено перебором всех 2 Задача о сумме Уже рассмотренная задача о сумме также является NP–полной, отметим, что если количество слагаемых фиксировано, то сложность задачи является полиномиальной, так как: o для 2-х слагаемых o для 3-х слагаемых Однако в общем случае придется перебирать 3 Задача о клике Пусть дан граф G = G(V,E), где V – множество из n вершин, а E – множество ребер. Будем понимать под кликой максимальный по количеству вершин полный подграф в графе в G. Задача состоит в определении клики в заданном графе G Поскольку в полном графе на m вершинах имеется m(m-1)/2 ребер, то проверка, является ли данный граф полным, имеет сложность O (
Однако в общем случае придется проверять все подграфы с количеством вершин m = (2, n) на их полноту и определить максимальное значения m для которого в данном графе G существует полный подграф, что приводит к оценке в худшем случае:
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 783; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.161.194 (0.013 с.) |

 , а задача 2 – множеством, и существует функция
, а задача 2 – множеством, и существует функция  (алгоритм), сводящая конкретную постановку задачи 2 (
(алгоритм), сводящая конкретную постановку задачи 2 ( ) к конкретной постановке задачи 1(
) к конкретной постановке задачи 1( ):
):  , то задача 2 сводима к задаче 1.
, то задача 2 сводима к задаче 1. (
(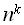 ), т.е. алгоритм сведения принадлежит классу P, то говорят, что задача 1 полиномиально сводится к задаче 2.
), т.е. алгоритм сведения принадлежит классу P, то говорят, что задача 1 полиномиально сводится к задаче 2.
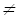 NP, то есть NP \ P
NP, то есть NP \ P 
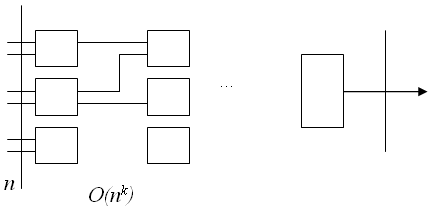
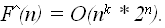 Для этой, как и для всех других NP–полных задач не известен полиномиальный алгоритм решения.
Для этой, как и для всех других NP–полных задач не известен полиномиальный алгоритм решения.
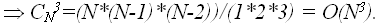
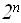 различных вариантов, так как по биномиальной теореме
различных вариантов, так как по биномиальной теореме 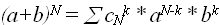 , а при a=b=1, имеем:
, а при a=b=1, имеем: 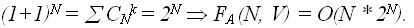
 ). Очевидно, что если мы рассматриваем подграф с m вершинами в графе G с вершинами (m < n), то всего существует
). Очевидно, что если мы рассматриваем подграф с m вершинами в графе G с вершинами (m < n), то всего существует 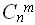 различных подграфов. Если в задаче о клике количество вершин клики фиксировано, то перебирающий алгоритм имеет полиномиальную сложность:
различных подграфов. Если в задаче о клике количество вершин клики фиксировано, то перебирающий алгоритм имеет полиномиальную сложность:




