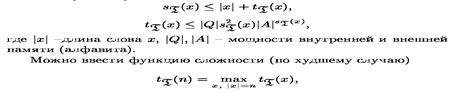Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Полиномиально проверяемые задачи.Содержание книги
Поиск на нашем сайте
Анализ алгоритма точного решения задачи о сумме Формулировка задачи и асимптотическая оценка Словесно задача о сумме формулируется как задача нахождения таких чисел из данной совокупности, которые в сумме дают заданное число, классически задача формулируется в терминах целых чисел [6]. В терминах структур данных языка высокого уровня задача формулируется, как задача определения таких элементов исходного массива S из N чисел, которые в сумме дают число V (отметим, что задача относится к классу NPC). Детальная формулировка: Тривиальное решение определяется равенством V=Sum, где Sum= Min {S[i], i=1,N} =< V =< Sum. Получим асимптотическую оценку сложности решения данной задачи для алгоритма, использующего прямой перебор всех возможных вариантов. Поскольку исходный массив содержит N чисел, то проверке на равенство V подлежат следующие варианты решений: o V содержит 1 слагаемое o V содержит 2 слагаемых o V содержит 3 слагаемых o и т.д. до проверки одного варианта с N слагаемыми. Поскольку сумма биномиальных коэффициентов для степени N равна -
2. Алгоритм точного решения задачи о сумме (метод перебора) Определим вспомогательный массив, хранящий текущее сочетание исходных чисел в массиве S, подлежащих проверке на V – массив Cnt[j], элемент массива равен «0», если число S[j] не входит в V и равен «1», если число S[j] входит в V Решение получено, если V = Могут быть предложены следующие две реализации механизма полного перебора вариантов: o перебор по всевозможным сочетаниям из k элементов по N, т.е. сначала алгоритм пытается представить V как один из элементов массива S, затем перебираются все возможные пары, затем все возможные тройки и т.д.; o перебор по двоичному счётчику, реализованному в массиве Cnt: Вторая идея алгоритмически более проста и сводится к решению задаче об увеличении двоичного счётчика в массиве Cnt на «1»: o при 00...0111 увеличение на «1» приводит к сбросу всех правых «1» и установке в «1» следующего самого правого «0»; o при 00...1000, когда последний элемент счетчика равен «0» увеличение на «1» приводит к переустановке последнего элемента в массиве Cnt с «0» в «1». Рассматривая массив Cnt как указатель на элементы массива S, подлежащие суммированию в данный момент, мы производим суммирование и проверку на V, до тех пор, пока решение не будет найдено или же безрезультатно будут просмотрены все возможные варианты. Таким образом, алгоритм точного решения задаче о сумме методом прямого перебора имеет в формальной системе языка высокого уровня следующий вид:
Анализ алгоритма точного решения задачи о сумме Рассмотрим лучший и худший случай для данного алгоритма: a.) В лучшем случае, когда последний элемент массива совпадает со значением V: V=S[N],необходимо выполнить только одно суммирование, что приводит к оценке: b. В худшем случае, если решения вообще нет, то придется проверить все варианты, и Получим детальную оценку для худшего случая, используя принятую методику подсчета элементарных операций:
Для получения значения
4* Очевидно, что для решения некоторой массовой проблемы можно придумать не один алгоритм. Поэтому важно иметь критерии, позволяющие оценивать разработанные алгоритмы. Временная сложность.
Тогда:
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 414; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.15.112 (0.006 с.) |

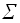 Sj=V
Sj=V вариантов;
вариантов; вариантов;
вариантов; вариантов;
вариантов; и для каждого варианта необходимо выполнить суммирование (с оценкой O(N)) для проверки на V, то оценка сложности алгоритма в худшем случае имеет вид:
и для каждого варианта необходимо выполнить суммирование (с оценкой O(N)) для проверки на V, то оценка сложности алгоритма в худшем случае имеет вид: (7.1)
(7.1) (N)=Q(N);
(N)=Q(N); (N) = Q (N*
(N) = Q (N*  ).
). +2+2} (7.2)
+2+2} (7.2)


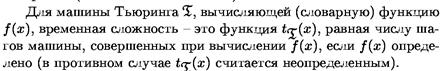 Время решения индивидуальной задачи зависит от скорости вычислителя, языка программирования и многого другого. Определяя качество алгоритма имеет смысл не учитывать эти факторы. Вместо времени мы будем оценивать количество характерных операций, которое необходимо выполнить, решая индивидуальную задачу данным алгоритмом.
Время решения индивидуальной задачи зависит от скорости вычислителя, языка программирования и многого другого. Определяя качество алгоритма имеет смысл не учитывать эти факторы. Вместо времени мы будем оценивать количество характерных операций, которое необходимо выполнить, решая индивидуальную задачу данным алгоритмом.