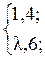Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическая логика и теория алгоритмовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
МАТЕМАТИЧЕСКАЯ ЛОГИКА И ТЕОРИЯ АЛГОРИТМОВ
ПОНЯТИЕ ОБ АЛГОРИТМАХ. СХЕМЫ АЛГОРИТМОВ
Схемы алгоритмов
Предписание о последовательности действий алгоритма может быть представлено так называемой схемой: логической схемой алгоритма, матричной схемой алгоритма, граф-схемой алгоритма. Логическая схема алгоритма (ЛСА) впервые была предложена советским математиком Ляпуновым А.А. (1911-1973 гг.) в бытность его профессором кафедры математики военной артиллерийской (в те годы) академии им. Ф.Э. Дзержинского [36]. ЛСА – это выражение, состоящее из символов операторов, логических условий, следующих в определенном порядке, а также нумерованных стрелок, расставленных особым образом. Матричная схема алгоритма (МСА) – это квадратная матрица, элементы которой указывают условия передачи управления от i-го оператора строки к j-ому оператору столбца. Строки матрицы нумеруются от первого оператора до предпоследнего, столбцы – от второго до последнего. Граф-схема алгоритма (ГСА) – это ориентированный граф особого вида. Он содержит вершины четырех типов: 1) операторные, обозначаемые прямоугольниками; 2) условные, обозначаемые ромбами; 3) начальную и 4) конечную вершины, обозначаемые овалами. Вершины соединяются дугами. Граф-схемы алгоритмов называют просто схемами и выполняют по ГОСТ 19.701-90 «Схемы алгоритмов, программ, данных и систем. Условные обозначения и правила выполнения». В табл. 68 приведены наименования, обозначения и определения отображаемых функций для символов, используемых при описании алгоритмов. Таблица 68 Описание символов, используемых в схемах алгоритмов
Символы могут быть вычерчены в любой ориентации, но предпочтительной является горизонтальная ориентация. Внутрь символа помещают обозначения или описания операций. Символы могут быть отмечены идентификаторами или порядковыми номерами. Идентификатор представляет собой букву или букву с цифрой и должен располагаться слева над символом. Направления линий связи слева направо и сверху вниз считаются стандартными, и линии связи изображаются без стрелок, в противоположном случае – со стрелками. Линии могут соединяться одна с другой, но не могут разветвляться. Алгоритм может быть реализован и схемой элементов (устройств), которые выполняются по ГОСТ 2.701-84 «Схемы. Виды и типы. Общие требования к выполнению». Рекурсивные функции Рекурсия – один из основных приемов программирования. Рекурсивные функции – функции, зависящие сами от себя. Когда мы рассматривали автоматы, то говорили о функциях переходов, которые в последующий момент автоматного времени зависят от своих значений в предыдущий момент времени. Так реализуется автоматная память. В теории рекурсивных функций, которая считается исторически первой формализацией понятия алгоритма, применяется нумерация слов в произвольном алфавите натуральными числами (N), и любой алгоритм сводится к вычислению некоторой функции при целочисленных значениях аргументов [22]. Функция вычислима, если существует такой алгоритм, то есть пошаговая процедура «от простого к сложному», которая по входному набору переменных вычисляет значение функции, если этот входной набор принадлежит к области определения функции, или выдает сообщение, что входной набор не принадлежит к области определения функции. Функция полувычислима, если при задании входного набора, не принадлежащего области определения функции, алгоритм не заканчивает работу («зацикливается»). Теорию вычислимости разрабатывал А. Черч. Идея была похожа на изученную нами проблему функциональной полноты переключательных функций: выделить элементарные вычислимые функции (которые «интуитивно вычислимы») – то есть базис и предложить средства получения из этих элементарных вычислимых функций более сложных функций за конечное число шагов (как принцип суперпозиции в теории переключательных функций). Полученные таким образом функции тоже будут вычислимы. Таковыми элементарными вычислимыми функциями являются: 1) S(x)=x+1, (N 2) 0(х)=0, константа нуля; 3) Im(x1x2…xn)=xm – проектирующая функция, результатом которой является выбор m-го из n аргументов. Для получения из одних полувычислимых функций других функций за конечное число шагов были предложены так называемые операторы. Первым из них является известный нам оператор суперпозиции, т.е. подстановка в функциюфункций вместо переменных. При этом увеличивается размерность функции. Вторым оператором является оператор примитивной рекурсии. Рассмотрим пример задания числового ряда Фибоначчи 1,1,2,3,5,8,13,21,… с использованием оператора примитивной рекурсии:
Здесь указываются два начальных значения функции f(0), f(1) и принцип формирования последующего значения. В отличие от функций переходов автомата, указывается не автоматное время, а шаг вычислений n, т.е. значение функции на некотором шаге, отличном от нулевого и первого, равно сумме значений функции на двух предыдущих шагах. Тогда f(0)=1, f(1)=1, f(2)=f(0)+f(1)=1+1=2, f(3)=f(1)+f(2)=1+2=3, f(4)=f(2)+f(3)=2+3=5,… Рассмотрим другой пример использования оператора примитивной рекурсии:
f(0)=1, f(1)=f(0)×1=1, f(2)=f(1)×2=2, f(3)=f(2)×3=6, … Таким образом, мы задали функцию факториала: x! Функции, получаемые из элементарных, путем конечного числа применений операторов суперпозиции и примитивной рекурсии, называются примитивно-рекурсивными. Рассматривается и более сложная рекурсия, например, кратная, по нескольким переменным одновременно [19]. Все ли функции являются примитивно – рекурсивными? Можно показать, что множество всех одноместных целочисленных функций типа N Третьим оператором является оператор минимизации m, который позволяет вводить в вычисления перебор для определения нужного значения. Например: f(x1x2)=m(y–x1=x2);
Напомним, что x1, x2 являются натуральными числами. Такие функции называются частично рекурсивными, то есть они не полностью определенные, в отличие от полностью определенных примитивно-рекурсивных. В соответствие с тезисом Черча функция полувычислима, если и только если она частично рекурсивна. Имеются невычислимые функции, в которых связь между входными и выходными величинами столь сложна, что невозможно задать строго определенный пошаговый процесс преобразования исходных данных в результат [36], т.е. нельзя построить алгоритм решения соответствующей задачи. Рекурсивные функции – основа функционального программирования. Примером языка функционального программирования является язык LISP, разработанный в 1960 г. Д Маккарти. Это один из первых языков обработки данных в символьной форме (LISP, от LISt Processing – обработка списков). Одним из наиболее существенных свойств языка LISP является то, что данные, программы и даже сам язык – представляют собой просто списки символов в скобках. Подобная структура позволяет писать программы или подпрограммы, способные обращаться сами к себе [37]. В LISP используется префиксная форма записи: (+ху)=x+y; (*х(+ху))=x*(x+y); (+(*хх)(*уу))=x2+y2. Определение функций и их вычисление в языке основано на так называемом лямбда-исчислении, введенном в 1931 г. А Черчем: λ(х1,х2,…,хn)fn или (lambda(xy)(+(*xx)(*yy))), где λ – определение функции, х1,…,хn – формальные параметры (лямбда список), fn – тело функции. Рекурсии присутствуют и в языках структурного программирования. Рассмотрим пример решения задачи на Паскале, использующий рекурсию [3]. З а д а ч а. Известно рекурсивное определение факториала:
Здесь n – неотрицательно. Записать эту функцию на языке Паскаль. Решение. В первой строке определения явно указано, как вычислить факториал, если аргумент равен нулю или единице. В любом другом случае для вычисления n! необходимо вычислить предыдущее значение (n-1)! и умножить его на n. Уменьшающееся значение гарантирует, что в конце концов возникнет необходимость найти 1! или 0!, которые вычисляются непосредственно. program task5; var n:integer; {исходное значение} function fact(i:integer):integer; begin if (i=1) or (i=0) then fact:=1 else fact:=fact(i-1)*i; end; begin write(’Введите нужное значение n ’); readln(n); writeln(’Факториал ’,n,’ равен ’,fact(n)); end. Заметим, что на время выполнения вспомогательного алгоритма основной алгоритм приостанавливается. При вызове новой копии рекурсивного алгоритма вновь выделяется место для всех переменных, объявляемых в нем, причем переменные других копий будут недоступны. При удалении копии рекурсивного алгоритма из памяти удаляются и все его переменные. Активизируется предыдущая копия рекурсивного алгоритма, становятся доступными ее переменные. Пусть необходимо вычислить 4!. Основной алгоритм: вводится n=4, вызов fact(4). Основной алгоритм приостанавливается, вызывается и работает fact(4): 4<>1 и 4<>0, поэтому fact:=fact(3)*4. Работа функции приостанавливается, вызывается и работает fact(3): 3<>1 и 3<>0, поэтому fact:=fact(2)*3. В данный момент в памяти компьютера две копии функции fact. Вызывается и работает fact(2): 2<>1 и 2<>0, поэтому fact:=fact(1)*2. В памяти компьютера уже три копии функции fact и вызывается четвертая. Вызывается и работает fact(1): 1=1, поэтому fact(1)=1. Работа этой функции завершена, продолжает работу fact(2). fact(2):=fact(1)*2=1*2=2. Работа этой функции также завершена, и продолжает работу функция fact(3). fact(3):=fact(2)*3=2*3=6. Завершается работа и этой функции, и продолжает работу функция fact(4). fact(4):=fact(3)*4=6*4=24. После чего управление передается в основную программу и печатается ответ: «Факториал 4 равен 24».
Машина Тьюринга
Машина Тьюринга – одна из абстрактных моделей алгоритмов названа в честь английского математика Алана Тьюринга (1912-1954 гг.). Машина Тьюринга включает [19]: 1) управляющее устройство, которое может находиться в одном из состояний, образующих конечное множество Y={y1,y2,...,yk}; 2) ленту, разбитую на ячейки, в каждой из которых может быть записан один из символов конечного алфавита Х={х1,х2,...,хp}; 3) устройство обращения к ленте – считывающую и записывающую головку, которая в каждый момент времени «обозревает» ячейку и, в зависимости от символа в ячейке и состояния управляющего устройства, записывает в эту ячейку новый символ (он может совпадать с прежним, считываемым) или пустой символ (прежний символ стирается и не его место записывается символ пробела). Далее устройство обращения сдвигается на ячейку влево или вправо или остается на месте. При этом управляющее устройство переходит в новое внутреннее состояние или остается в старом (текущем) состоянии. Среди состояний устройства управления выделяются начальное y1 и заключительное yk состояния (k – мнемонический знак окончания работы). В начальном состоянии машина Тьюринга находится перед началом работы, в конечном – после окончания работы. Память машины Тьюринга – конечное множество состояний (внутренняя память) и лента (внешняя память). Лента бесконечна в обе стороны, однако в начальный момент времени только конечное число ячеек ленты заполнено символами, остальные пусты, т.е. содержат пустой символ – символ пробела l. Данные машины Тьюринга – слова в алфавите ленты, на ленте записываются исходные данные и затем – результат. Элементарные шаги – это считывание и запись символов, сдвиг головки, переход устройства управления из состояния в состояние. На рис. 88 изображена структурная схема машины Тьюринга. Под воздействием входного символа х, например 1, считываемого головкой, устройство управления формирует выходной символ Z, управляет движением головки: влево (L), вправо (R), на месте (Е).
Рис. 88. Структурная схема машины Тьюринга
Полное состояние машины или конфигурация (или машинное слово), по которому однозначно определяется ее дальнейшее поведение, описывается внутренним состоянием yi, символами слева и справа от головки, например:...x1yix2... Система команд машины содержит записи вида Совокупность всех команд называется программой. Каждая машина Тьюринга определяется своим алфавитом, состояниями внутренней памяти и программой. Чтобы полностью определить работу машины, надо указать ее конфигурацию для начального момента времени. Будем считать, что в начальной конфигурации головка воспринимает самую левую непустую ячейку. Машина Тьюринга задается тройкой – М=<X,Y,П>, где Х – алфавит символов ленты с выделенным пустым символом l (пробелом); Y – алфавит внутренних состояний с выделенными символами начального y1 и конечного yk состояний; П – программа, т.е. конечная последовательность упорядоченных пятерок символов – команд. Если машина, начав работу с некоторым словом, записанным на ленте, приходит в заключительное состояние, то она называется применимой к этому слову. Результатом ее работы считается слово, записанное на ленте в заключительном состоянии. Если же машина ни в какой момент времени не приходит в заключительное состояние, то она называется не применимой к данному слову и результат ее работы не определен. Пример 1. Рассмотрим машину Тьюринга, алфавит ленты которой содержит кроме символов пробела l символ 1. Будем представлять некоторое число «а» в виде а символов 1, например, l111l – число 3, l11111l – число 5. Машина, увеличивающая записанное число на единицу и возвращающаяся в исходное положение, реализуется следующей программой:
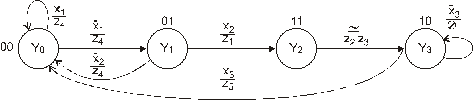
Работа машины может быть описана графом переходов (рис. 89), в котором дуги помечены условиями переходов (числитель), записываемыми символами и указанием направления движения головки (знаменатель).
Рис. 89. Граф переходов машины Тьюринга, реализующий алгоритм увеличения числа на единицу
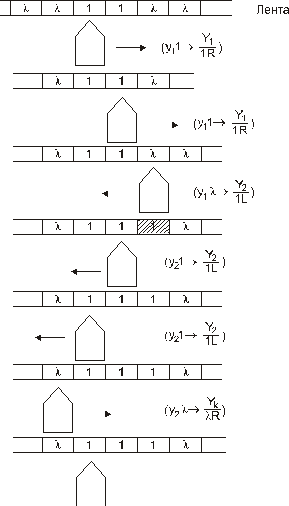
Последовательность работы машины, например, для слова l11l, описывается рис. 90. Вначале (исходное положение) головка находится у начала числа и по окончании работы должна установиться там же – у начала числа, увеличенного на 1.
Рис. 90. Последовательность работы машины Тьюринга, реализующей алгоритм увеличения числа на единицу
Такая машина применима к любому слову в алфавите {l,1}. Работа машины Тьюринга может быть описана таблицей (табл. 69).
Таблица 69 Работа машины Тьюринга
Строку с yk можно опустить. В табл. 69 xi – выходной символ, StÎ{L,R,E}. Пример 2. [19]: Рассмотрим пример реализации алгоритма сложения чисел а и b, записанных на ленте в виде а и b единиц с разделителем *. Обозначим такую запись 1а, 1b. Следовательно, необходимо переработать слово 1а*1b в слово 1а+b, т.е. удалить разделительный символ * и сдвинуть одно из слагаемых, скажем, первое ко второму (как на счетах). Такой алгоритм осуществляет машина Тьюринга, граф переходов устройства управления которой изображен на рис. 91. Здесь в числителе – считываемый символ, в знаменателе – записываемый символ и знак управления движением головки.
Рис. 91. Граф переходов машины Тьюринга, реализующей алгоритм сложения двух чисел, заданных единицами
Пусть, например, заданы числа 12 и 11. Тогда последовательность работы машины может быть описана рис. 92. В исходном положении головка установлена напротив начала первого числа (напротив первой его единицы). Головка на месте первой единицы записывает пробел l и движется до разделителя *, найдя который, записывает вместо него 1 и начинает движение влево, останавливается напротив первого пробела, а затем сдвигается вправо к первой единице. На графе рис. 91 переход
Рис. 92. Последовательность работы машины Тьюринга, реализующей сложение чисел 12(11) и 11(1)
Тогда система команд имеет вид:
Аналогично могут быть построены некоторые другие простые машины Тьюринга, в том числе машина для разветвления алгоритма, организации цикла и т.д. Из простых машин Тьюринга можно простроить более сложные путем композиции. А. Тьюринг выдвинул следующую гипотезу. Тезис Тьюринга. Всякий интуитивный алгоритм может быть реализован с помощью некоторой машины Тьюринга. Как показывает опыт, любые действия, которые может выполнить вычислитель-человек, могут быть представлены последовательностью действий некоторой машины Тьюринга. Частичная числовая n-местная функция f(x1,...,xn) называется вычислимой по Тьюрингу, если существует машина, вычисляющая ее в следующем смысле: 1. Если набор значений аргументов принадлежит области определения функции f, то машина, начав работу в некоторой конфигурации, задающей значение аргументов, останавливается, заканчивая работу в конфигурации, соответствующей значению функции. 2. Если набор значений аргументов не принадлежит области определения функций f, то машина, начав работу в некоторой конфигурации, работает бесконечно, не приходя в заключительное состояние. Машина Тьюринга – идеализированная модель ЭВМ. Она намного проще даже самых первых примитивных ЭВМ. Но для теоретических исследований она слишком громоздка. Поэтому получили распространение усовершенствования машины Тьюринга, одним из которых является многоленточная машина Тьюринга (рис. 93). Она имеет несколько входных лент и одну выходную, на которую записывается результат. Содержимое ячеек выходной ленты нельзя читать и корректировать. В такой машине полагается, что головки неподвижны, а ленты движутся, возможно в разных направлениях [36]. Такт работы это: одновременное считывание символов со всех лент, кроме выходной, смена состояния в зависимости от считанного набора символов, запись новых символов, сдвиг лент.
Рис. 93. Многоленточная машина Тьюринга Машина Поста Эмиль Пост – молодой американский математик – в 1936 г. предложил эту модель практически одновременно с А. Тьюрингом В его машине тоже имеется бесконечная лента и головка. Лента разделена на ячейки. В каждой ячейке записан один символ из фиксированного алфавита. В любой момент времени машина обрабатывает ровно одну ячейку. Машина Поста работает под управлением программы. Программа состоит из команд. Команды отличаются от команд машины Тьюринга. Если у Тьюринга все команды одного типа и похожи на функции переходов-выходов автомата, то у Поста команды больше напоминают машинные команды современных ЭВМ. Команды машины Поста состоят из трёх частей (полей) [7]: 1. Номер команды. 2. Операция. 3. Отсылка (номер следующей команды). Команды нумеруются с 1. Первой выполняется команда 1. Операции: 1. → – движение на одну клетку вправо (R). 2. ← – движение на одну клетке влево (L). 3. S – запись в обозреваемую ячейку, при этом предыдущее значение ячейки теряется (S – произвольный символ алфавита). 4. Ветвление
Si – символ в ячейке, М – номер следующей команды. 5. Стоп: HLT (ЕND). При ветвлении символы Si должны быть различны, но не обязательно использовать весь алфавит. Если Si есть в ячейке, то выполняется команда Mi, при этом головка не перемещается и в клетку ничего не записывается. Если ни один символ не совпадает – происходит так называемая безрезультатная остановка. Пример 1. Алфавит А: {1,λ}, где λ – пустой символ, как и в машинах Тьюринга. 1. R,2; 2. 1,1. Это программа заполнения ленты символами 1, т.е. пустой ленты, в которой во всех ячейках – λ. Пример 2. Прибавление символа 1 к числу 11...1, А={λ,1}. 1. R,2; 2. 3. 1,4; 4. HLT. Это программа так называемого инкремента, то есть число, записанное «зарубками», «черточками», увеличивается на одну «черточку» при движении вправо. Если же после прибавления двигаться влево к началу числа, как это обычно требуется, то: 4. L,5; 5. 6. λ,7; 7. R,8; 8. HLT. Если работа алгоритма никогда не закончится над некоторыми исходными данными, то алгоритм неприменим к ним (хотя в примере 1 это и не так). Алгоритм А над исходными данными X обозначим А(Х) – это результат работы алгоритма. Результат не определен, если А неприменим к Х. Э. Пост выдвинул предположение, что для всякого алгоритма, в котором исходными данными и результатами являются слова, существует эквивалентная ему машина Поста. Постовые алгоритмы – это алгоритмы, работающие со словами. В принципе, все математические объекты можно закодировать в виде слов. Проблема самоприменимости Объектом изучения в теории алгоритмов является, прежде всего, алгоритмическая разрешимость некоторой массовой задачи [19]. Разрешимая задача – для которой имеется абстрактная модель, за конечное число шагов проверяющая для любых входных данных, имеется ли решение данной задачи. Напомним, что машина называется применимой к начальному слову, если она, начав работать с этим словом, придет в заключительное состояние. Пример неприменимой машины – машина Тьюринга, у которой в первой части команд не встречается заключительное состояние yk. Машина М1, применимая к слову n(M1), т.е. к коду своего собственного номера, называется самоприменимой. Предполагается, что машина Тьюринга универсальна, она читает код своего номера (программы), с ленты, расшифровывает его и в соответствии с ним выполняет необходимые действия в зависимости от начальной конфигурации (данных), также записанные на ленте. Машина, не применимая к слову n(M), называется несамоприменимой. Проблема самоприменимости (впервые эта проблема рассмотрена отечественным математиком О.Б. Лупановым [24]) заключается в том чтобы по заданной программе Р для абстрактной машины узнать, применима ли она к своей собственной записи Р((Р)), где (Р) – запись программы или подпрограммы n(P) [7]. Например, программа машины, заменяющей символы 1 на 0, а 0 на 1, применима к любому слову, в частности и к своей записи, если мы закодируем записи программ в двоичном коде, что вполне возможно, поэтому она самоприменима, а программа В: B: 1)?{l,2}; 2) HLT, применима только к пустому слову, т.е. несамоприменима. В машине В, если головка в начальный момент обозревает ячейку, в которой записан не пробел l, то произойдет безрезультатная остановка. Задача заключается в отыскании такого алгоритма, который определял бы для любой программы ее самоприменимость. Сложность алгоритма
Сложность алгоритма отражает затраты, требуемые для его работы. Будем рассматривать временную сложность. Это функция, которая каждой входной длине n ставит в соответствие минимальное время, затрачиваемое алгоритмом на решение всех однотипных индивидуальных задач этой длины [24]. Из курса математического анализа известно, что функция f(n) есть О(g(n)), если существует константа с такая, что |f(n)|£c(g(n)) для всех n³0 [19]. O(n) – сложность порядка n, n – параметр исходных данных алгоритма. O(n2) – сложность порядка n2. Сложность бывает минимальной, средней и максимальной. Сложностью задачи называется сложность наилучшего алгоритма. Полиномиальным алгоритмом (или алгоритмом полиномиальной временной сложности) называется алгоритм, у которого временная сложность равна О(Р(n)), где Р(n) – некоторая полиномиальная функция от входной длины n. Алгоритмы, для временной сложности которых не существует такой оценки, называются экспоненциальными. Задача считается труднорешаемой, если для нее не существует разрешающего полиномиального алгоритма. Итак, основные классы сложности таковы: а) Полиномиальная сложность. P(n) – полином от n. O(P(n)) – сложность задач класса Р. Полиномиальные задачи: степень полинома не зависит от n. Например: O(P(n)) – линейная, O(P(n2)) – квадратичная, O(P(n3)) – кубическая. Такие задачи легко решаются на ЭВМ. б) Экспоненциальная сложность. O(xn) – класс Е – экспоненциальный. Например: O(2n) – построение булеана, O(22n) – нахождение всех переключательных функций от n переменных. При больших n задача становится практически нерешаемой. в) NP сложные задачи [36]. Вспомним задачу коммивояжера из теории графов. Перебор всех маршрутов в графе из n вершин требует рассмотрения n! вариантов. Однако, n! растет даже быстрее, чем 2n. В так называемом недетерминированном алгоритме (существует и недетерминированная машина Тьюринга) варианты выбираются случайным образом, тогда, если повезет, можно относительно быстро найти вариант, удовлетворяющий заданным ограничениям [36]. Такие задачи, имеющие недетерминированное решение, которое иногда удается найти за полиномиальное время называются NP-сложными (Nondeterministic Polynomial). Преобладает мнение, что детерминированных алгоритмов решения таких задач не существует. Для сокращения перебора вариантов при решении таких комбинаторных задач (задач комбинаторной сложности) предлагаются различные способы «борьбы с перебором, борьбы с проклятием размерности» [9-10]. В эвристических алгоритмах используют для этого некоторую дополнительную информацию – эвристики, позволяющие находить решения, лишь на 10-15 % хуже оптимальных. Тем не менее, NP сложные задачи не имеют гарантированных оценок времени решения. Даже незначительное изменение исходных данных приводит к его резкому увеличению. Поэтому иногда говорят, что проблема NP полна, что означает ничтожно малую вероятность существования эффективного (полиномиального) алгоритма. В настоящее время активно развивается направление так называемых генетических алгоритмов. Это направление использует в борьбе с перебором вариантов опыт развития природы и человека. При этом применяется и соответствующая терминология: «популяция» – некоторое множество вариантов; «скрещивание» вариантов путем определенного комбинирования «хромосом особей» из исходной популяции и получение «потомков»; «эволюция» с целью получения лучших решений.
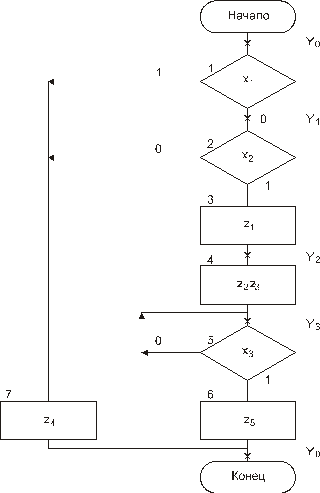
Рис. 96. Некоторая ГСА
В таблице программирования табл. 72 левая часть, соответствующая коду дуги – это обобщенный адрес ячейки памяти, правая часть – данные, записанные по этому адресу. Таблица 72 Таблица программирования ПЗУ
Для получения полной таблицы программирования, в которой будет 25=32 строки, необходимо составить развернутую таблицу (табл. 73) и затем доопределить адреса ПЗУ. Для компактности целесообразно записывать адреса и данные в восьмеричной системе счисления. Таблица 73 Развернутая таблица программирования ПЗУ в восьмеричной системе счисления
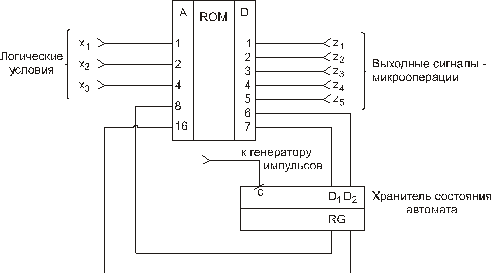
Функциональная электрическая схема автомата на ПЗУ, реализующего заданную (рис.96) ГСА, изображена на рис. 97.
Рис. 97. Автомат на основе ПЗУ
На рис. 97 код состояния автомата фиксируется регистром RG, который тактируется генератором тактовых импульсов (изменение состояния автомата происходит по тактовым импульсам). Недостатком автомата на базе ПЗУ является большой объем памяти, необходимой при большом количестве логических условий. Сократить объем памяти ПЗУ можно путем использования так называемых мультиплексоров, или коммутаторов каналов, позволяющих в каждом состоянии проверять только одно или несколько (не все сразу) логических условий. В этом случае будут особенности отметки ГСА (при получении ОГСА). Если за условной вершиной следует условие, с целью проверки только одного условия метка ставится после данной условной вершины. В остальном разметка ГСА не отличается от разметки для автомата без мультиплексора. Эти особенности обуславливаются требованиями проверки в каждом такте (на каждом переходе) не более одного логического условия. Рассмотрим получение автомата на ПЗУ и мультиплексоре для той же ГСА (рис. 96), но с другой разметкой (рис. 98).
Рис. 98. ОГСА для автомата на ПЗУ и мультиплексоре
Видно, что переход от метки к метке осуществляется с проверкой не более одного логического условия. Далее обычным образом строится граф автомата (рис. 99).
Рис. 99. Граф переходов а |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 470; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.103.70 (0.013 с.) |













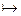 N), функция следования (указывает следующее натуральное число);
N), функция следования (указывает следующее натуральное число);
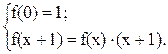



 , где х1 – читаемый символ в состоянии y1; y2 – новое внутреннее состояние; l – записываемый символ; R – признак продвижения головки, ® – символ перехода в новое состояние.
, где х1 – читаемый символ в состоянии y1; y2 – новое внутреннее состояние; l – записываемый символ; R – признак продвижения головки, ® – символ перехода в новое состояние. ;
;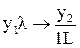 ;
; ;
; .
.






 необходим для случая отсутствия первого числа, т.е. когда исходное слово имеет вид *1b.
необходим для случая отсутствия первого числа, т.е. когда исходное слово имеет вид *1b.