
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о математической лингвистикеСодержание книги
Поиск на нашем сайте
Язык – важнейшее средство человеческого общения – социальное средство хранения и передачи информации, одно из средств управления человеческим поведением. До начала XX в., говоря о языках, имели в виду только естественные языки (русский, английский и т.д.). В конце прошлого века была предпринята попытка создать искусственный язык – Эсперанто. Лингвистика – наука о языках – сводилась в основном к изучению конкретных естественных языков, их классификации, выяснению сходств и различий между ними. Возникновение математики, логико-философского исследования языка науки, привели к появлению идеи структуралистского подхода к лингвистике [19]. Язык может быть описан математическими средствами, как преобразование некоторых абстрактных объектов – смыслов, в некоторые объекты – тексты и обратно [29]. Преобразование объектов языка выглядит следующим образом: 1) переход от смыслов к синтаксическим структурам без линейного порядка; 2) переход к линейным последовательностям слов; 3) получение цепочек звуков. Язык – частный случай знаковой системы. Наиболее хорошо исследованы знаковые системы, в которых знаками являются символы алфавитов, а последовательностями знаков – тексты; к таким знаковым системам относятся естественные языки, языки науки, а так же сильно развившиеся за последние 60 лет языки программирования. Математическая лингвистика – математическая дисциплина, предметом которой является разработка формального аппарата для описания строения естественных и некоторых искусственных языков. Математическая лингвистика является ответвлением математической логики. Наибольших успехов математическая лингвистика достигла в изучении синтаксиса, где за последние годы сложился специальный математический аппарат – теория формальных языков и грамматик. Формальный язык Формальный язык в отличие от естественного, допускающего неоднозначность, двусмысленность, строится по математически строгим и точным правилам. Он применяется для описания искусственных языков, например, языков программирования. Задается алфавит V={a,b,c,….x,y,z}, состоящий из букв или символов [4]. Иногда буквы нумеруют, как в алфавите русского языка «а» – первая буква, «я» – последняя. Тогда Vk – множество слов из k букв. Цепочки. Слово ωÎVk называется еще цепочкой ω. Длина цепочки обозначается |ω|. При k=0 получаем пустое слово, обозначаемое l. |l|=0. V* – множество всех слов – эквивалент универсума в теории множеств. Нетрудно видеть, что V* счетно. Пусть V={а,b}. Будем нумеровать слова [4]: а=1, b=2, аа=3=(1×21+1×20), аb=4=(1×21+2×20), bа=5=(2×21+1×20), bb=6=(2×21+2×20) и т.д. Получилась так называемая лексико-графическая нумерация. Таким образом, по каждой цепочке можно получить ее номер. У пустой цепочки номер 0. По номеру можно получить цепочку в заданном алфавите. Пусть V={а,b,с}. Получим цепочку №20. Предварительно введем таблицу формирования номера в таком алфавите (табл. 89). Таблица 89 Формирование номера цепочки в V={а,в,с}
Тогда 20=9+9+2, то есть (1×32+3×31+2×30), получаем цепочку асb. Подобным образом можно нумеровать и другие объекты. Получим, например, номер формулы логики высказываний А®В. Алфавит: {А,В,®,¯}, тогда номер цепочки: (1×32 +3×31+2×30)=20. В этой цепочке старший (левый) разряд А, номер символа А в алфавите равен 1, вес его =32; следующий символ ®, номер символа ® равен 2, вес его =31; младший (правый) символ В, номер символа В равен 3, вес =30. Ясно, что не все номера представляют собой правильные формулы. Например, формула ®АВ – неправильная. Хотя в случае использования так называемой префиксной формы записи (символ бинарной операции ставится перед символами переменных – это польская инверсная запись ПОЛИЗ) эта формула будет правильной. Получим номер автомата – распознавателя последовательности 0132 в алфавите {0,1,2,3}: (1×33+2×32+4×31 +3×30)=60. Получим номер алгоритма по его логической схеме: Получим номер модуса Barbara в виде ааа1 (1 – номер фигуры) в алфавите {a,i,e,o,1,2,3,4}, где буква – вид суждения, цифра – номер модуса: (1×83+1×82+1×81 +5×80)=589. Над цепочками вводятся операции, например: · конкатенации ½½ (сцепления), например, аb½½bc=аbbс; · итерации * (повторения), например: а(bbа)*=аbbаbbаbbа…; · инверсии · циклического сдвига W (циклической перестановки символов), например, влево: W(аbс)=bса, или вправо: (аbс)W=саb; · перестановки групп символов (подцепочек данной цепочки), например, Q(ав(вс)(ав))=ававвс; · замены одной подцепочки данной цепочки другой цепочкой: (аbbс,bbÞd)=adc. Ранее мы упоминали о генетических алгоритмах. В них цепочками представляются некоторые варианты решения комбинаторной задачи. Такие цепочки называют как в генетике – хромосомами. В процессе «скрещивания» двух хромосом образуется новая хромосома, то есть цепочка, состоящая из частей «родительских» цепочек. В дальнейшем в процессе «эволюции» остаются или «выживают» только самые жизнеспособные, т.е. лучшие варианты. Так происходит и в природе. Все мы носим эти цепочки хромосом с собой и, возможно, передадим их частички в будущее. Не будем забывать заветы великого Дарвина: «Выживает сильнейший», в смысле – умнейший. Хотя, точнее, – тот, кто приспосабливается к изменениям. Операции над языками. Формальный язык L в алфавите V – это некоторое подмножество: V* LÍV*. Над языками, как над множествами вводятся теоретико-множественные операции: объединение, пересечение, разность. На декартово произведение похоже соединение (конкатенация) языков, например: L1={па,ма,да}, L2={па,к}, тогда L1×L2={папа,пак,мапа,мак,дапа,дак}. Очевидно, что L22={па,к}×{па,к}={папа,пак,кпа,кк}. Имеется также операция подстановки языка в язык [19]. Пусть заданы языки сумм: Lcm={а,а+а,а+а+а,…} и произведений Lnp={а,аа,ааа,…}. Подстановка Lcm(а®Lnp) дает язык сумм произведений Lcn={аа,ааа,…аа+а,…}. Итерация языка – это объединениевсех его степеней:
Определение языков – это их задание. Оно осуществляется следующими способами: · перечислением всех правильных цепочек языка; · порождением всевозможных цепочек и их «фильтрацией» с помощью так называемых распознавателей, которые распознают требуемые цепочки; · заданием соответствующей формальной грамматики, определяющей правила построения языка. Рассмотрим формальные грамматики.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 437; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.241.235 (0.01 с.) |

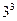



 в алфавите {
в алфавите { 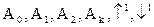 }:
}: 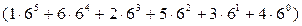 =16186.
=16186. (реверса), например,
(реверса), например,  ;
;



