Умозаключения путем противопоставления предикату.

Противопоставление предикату – это такое непосредственное умозаключение, при котором предикатом становится субъект, а субъектом понятие противоречащее предикату исходного суждения, причем связка меняется на противоположную:

S есть P	или	S не есть P
`P не есть S	`P есть S

 

То есть, сначала проводится превращение, а затем обращение (табл. 83*).

Таблица 83

Противопоставление предикату

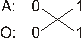
Пример (рис. 115).

Все студенты сдают экзамены.

Ни один не сдающий экзамен не является студентом.

Рис. 115. Пример противопоставления предикату

Непосредственное умозаключение может основываться и на отношениях между суждениями.

Такие умозаключения выстраиваются по логическому квадрату, если есть одиночная связь между соответствующими значениями истинности.

Если связь неоднозначная, то суждение правильно, если двигаться по ребру, определяющему однозначную связь, например, от O (0) к I (1).

 

13.3. Опосредованное дедуктивное умозаключение.

Фигуры силлогизма

 

Если посылки и вывод в опосредованном дедуктивном умозаключении являются простыми категорическими суждениями, то такое суждение называется простым категорическим силлогизмом (ПКС). В структуре простого категорического силлогизма имеются две посылки и вывод.

Для того чтобы между посылками и выводом было отношение следования они должны включать общие понятия. Такие общие понятия называются средним термином (М).

Понятие, которое входит в одну из посылок и стоит на месте субъекта в выводе называется субъектом простого категорического силлогизма (S).

Понятие, которое входит в одну из посылок и в вывод и стоит на месте предиката в выводе называется предикатом простого категорического силлогизма (Р).

Посылка, содержащая предикат и средний термин, – большая посылка (БП), которая стоит на первом месте.

Посылка, содержащая субъект и средний термин – меньшая посылка (МП), которая стоит на втором месте.

Вывод содержит субъект и предикат.

Структура ПКС:

БП:	(М, Р)
МП:	(M, S)
Вывод	(S, P)

Правила ПКС [8]:

1. Правила посылок.

а) по крайней мере, одна из посылок должна быть суждением общим. Из двух частных посылок вывод невозможен;

b) если одна из посылок суждение частное, вывод будет частным;

c) по крайней мере, одна из посылок должна быть суждением утвердительным. Из двух отрицательных суждений вывод невозможен;

d) если одна из посылок суждение отрицательное, вывод будет отрицательным.

2. Правила терминов.

a) в ПКС может быть только 3 термина (M, S, P);

b) средний термин должен быть распределен, по крайней мере, в одной из посылок;

c) термин, не распределенный в посылках, не может быть распределен в заключении.

Фигуры ПКС.

В зависимости от положения среднего термина в посылках получают 4 варианта ПКС, которые называются фигурами ПКС:

На основе общих правил ПКС могут быть выведены правила для каждой фигуры.

Для I фигуры: большая посылка – общее суждение, меньшая – утвердительное суждение.

Для II фигуры: большая посылка – общее суждение, а одна из посылок и вывод – отрицательные суждения.

Для III фигуры: меньшая посылка – утвердительное суждение, вывод – частное суждение.

Для IV фигуры: если большая посылка – утвердительное суждение, то меньшая – общее суждение; если одна из посылок – отрицательное суждение, то большая посылка – общее суждение.

В фигуре I вывод может быть любым суждением.

В фигуре II вывод только отрицательный.

В фигуре III только частный вывод.

Фигура IV редко находит применение в логике.

Примеры.

Для фигуры I: «Все металлы электропроводники, медь – металл, следовательно, медь является электропроводником».

MaP	{все металлы электропроводники}
saM	{медь – металл}
saP	{медь является электропроводником}

Для фигуры II: «У любого квадрата все стороны равны, у данного прямоугольника стороны не равны, следовательно, данный прямоугольник не квадрат».

Для фигуры III: «Все партии являются политическими организациями, некоторые организации выражают интересы предпринимателей, следовательно, некоторые организации, выражающие интересы предпринимателей, являются партиями».

Для фигуры IV: «Все студенты – учащиеся, все учащиеся – люди, некоторые люди – студенты».

Модусы ПКС.

Каждый из возможных вариантов простых суждений, из которых строятся ПКС, называется модусом ПКС. Чаще всего рассматривается 19 правильных модусов для ПКС [8].

1) AAA, EAE, AII, EIO;

2) EAE, AEE, EIO, AOO;

3) AAI, EIO, IAI, OAO, AII, EAO;

4) ААI, AEE, IAI, EAO, EIO.

Для простоты запоминания все 19 модусов имеют названия, объединенные в латинский стих:

I B a rb a r a, C e l a r e nt, D a r ii, F e r io que prioris,

II C e s a r e, C a m e str e s, F e st i n o, B a r o k o, secundae,

III tertia, D a r a pt i, D i s a m i s, D a t i s i, F e l a pt o n,

B o c a rd o, F e r i s o n habet, quarta insuper addit

IV Br a m a nl i p, C a m e n e s, D i m a r i s, F e s a p o, Fr e s i s o n.

Эти модусы можно проверить, построив диаграммы Эйлера для всех вариантов отношений между суждениями. Иногда рассматривают 5 дополнительных модусов: B a rb a r i, C e l a r e nt (I фигура), C a m e str o p, C e s a r o (II фигура), C a m e n e s (IV фигура).