
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Очевидно, что квантор общности может быть заменен конъюнкцией по предметной области, возможно бесконечной, А квантор существования – дизъюнкцией.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Пусть задан двухместный предикат «Решать задачи» на множествах: Мх={1,2} – множество студентов, Му={1,2} – множество задач. Тогда возможны следующие варианты для одного квантора: 1) $xР(х,у)=P(1,y)ÚP(2,y) – «Хотя бы 1 студент решает задачи»; 2) $yР(х,у)=Р(х,1)ÚР(х,2) – «Хотя бы одна задача решается студентами»; 3) "xР(х,у)=Р(1,у)×Р(2,у) – «Каждый студент решает задачи»; 4) "yР(х,у)=Р(х,1)×Р(х,2) – «Каждая задача решается студентами». Очевидно, что эти формулы не замкнутые, т.е. в зависимости от значений переменных они могут принимать различные значения истинности. Для возможных комбинаций двух кванторов получаем соответствующие замкнутые формулы. Для одноименных кванторов: 5) $x$yР(х,у)=Р(1,1)ÚР(2,1)ÚР(1,2)ÚР(2,2)=$y$xР(х,у) – «Существуют студенты, решающие хотя бы одну задачу», или, что то же самое, «Существуют задачи, решаемые хотя бы одним студентом»; 6) "x"yР(х,у)=Р(1,1)×Р(2,1)×Р(1,2)×Р(2,2)="y"xР(х,у) «Каждый студент решает каждую задачу» или, что то же самое, «Каждая задача решается каждым студентом». Для разноименных кванторов: 7) $x"yР(х,у)=Р(1,1)×Р(1,2)ÚР(2,1)×Р(2,2) – (x=1) (x=2) «Существуют студенты, решающие каждую задачу»; Ясно, что при перестановке кванторов получается совсем другой смысл: 8) "y$xР(х,у)=[Р(1,1)ÚР(2,1)]×[Р(1,2)ÚР(2,2)] – (y=1) (y=2) «Каждый студент решает хотя бы одну задачу»; 9) "x$yР(х,у)=[Р(1,1)ÚР(1,2)]×[Р(2,1)ÚР(2,2)] – (x=1) (x=2) «Каждая задача решается хотя бы одним студентом». Наоборот: 10) $y"xР(х,у) = Р(1,1)×Р(2,1)ÚР(1,2)×Р(2,2) – (y=1) (y=2) «Существуют задачи, решаемые каждым студентом». Таким образом, нетрудно показать что из $x"yР(х,у) следует "y$xР(х,у), т.е. из суждения «по меньшей мере один студент решил все задачи» следует суждение «каждую задачу решил по меньшей мере один студент» [25]. Действительно:
Аналогично доказывается то, что из $y"xР(х,у) следует "x$yР(х,у) т.е. из суждения «по меньшей мере одна задача решена каждым студентом» следует суждение «каждая задача решена по меньшей мере одним студентом». Таким образом, одноименные кванторы можно менять местами: $x$yР(х,у)=$y$xР(х,у); " Разноименные кванторы нельзя менять местами, но: $x"yР(х,у)®"y$xР(х,у); $y"xР(х,у)®"x$yР(х,у). Рассмотрим другие равносильности: Квантор общности может быть перенесен через конъюнкцию:
Квантор существования может быть перенесен через дизъюнкцию:
Кроме того, очевидны равносильности [29]:
17.3. Тождественные преобразования формул Формулы логики предикатов часто представляют в стандартной форме, например, в клаузальной. Формула в клаузальной форме (в виде конъюнкции – КНФ-дизъюнктов) явно использует лишь операции дизъюнкции, конъюнкции и инверсии, а каждый дизъюнкт – лишь операцию дизъюнкции и инверсии, причем инверсия применяется не более чем к одной предикатной букве (литере, литералу). Поэтому для представления произвольной формулы в форме дизъюнкта необходимо исключить все остальные логические операторы (включая кванторы) и уменьшить область действия знака отрицания до одной предикатной буквы [29].
|
||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 509; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |



 .
. .
. , где F – не содержит x;
, где F – не содержит x;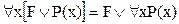 , где F – не содержит x;
, где F – не содержит x; , где F – не содержит x;
, где F – не содержит x; , где F – не содержит x.
, где F – не содержит x.


