Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Универсальная абстрактная машинаСодержание книги
Поиск на нашем сайте
Алгоритмы строятся из команд, а из алгоритмов можно строить более сложные алгоритмы [7]. 1) Композиция C алгоритмов А, В: C=А◦В С=В(А(Х)), Х – исходные данные. Таким образом, приписывается программа к программе (программа за программой). 2) Ветвление: А, В, С, D. Запускается алгоритм А. Если результат применения А(Х) соответствует заданному условию, то D(Х)=B(Х). Иначе, D(Х)=С(Х). 3) Итерация (повторение): Повторение алгоритма А, пока алгоритм В не укажет, что пора заканчивать. Более удобна, чем примитивные вышерассмотренные, так называемая универсальная машина U, которая выполняет, как и современная ЭВМ любую программу. Такая машина читает произвольную запись программы Р и применяет ее к заданному слову. Таким образом, исходные данные – это запись программы Р и исходные данные Х. (Р) – запись программы; Х – исходные данные (на ленте); (Р)*Х, где * – разделитель, символ не используемый в Р. Тогда результат записывается как U((P)*X)=P(X). Один из способов построения универсальной машины – использование геделевской нумерации алгоритмов [19]. Программу машины Тьюринга можно закодировать следующим образом. Представим в общем, виде команду:
где k – число программ (машин), S1=L – налево, S2=R – направо, S3=E – на месте. Пусть р1, р2, р3, ... последовательность всех простых чисел, расположенных в порядке возрастания (т.е. последовательность 2,3,5,7,11,...). Номером машины Тьюринга М с программой n называется число:
Закодируем, например, машину Тьюринга М1 с программой:
Здесь алфавит X0={1,l}, Y0={y1,yk}, кроме того t={1,2,3} соответствует L, R, E. Таким образом:
Естественно, не все натуральные числа являются номерами машин Тьюринга. Если n – номер некоторой машины, то ее программу можно однозначно установить по этому номеру.
Разрешимость в теории алгоритмов. Проблема самоприменимости Объектом изучения в теории алгоритмов является, прежде всего, алгоритмическая разрешимость некоторой массовой задачи [19]. Разрешимая задача – для которой имеется абстрактная модель, за конечное число шагов проверяющая для любых входных данных, имеется ли решение данной задачи. Напомним, что машина называется применимой к начальному слову, если она, начав работать с этим словом, придет в заключительное состояние. Пример неприменимой машины – машина Тьюринга, у которой в первой части команд не встречается заключительное состояние yk. Машина М1, применимая к слову n(M1), т.е. к коду своего собственного номера, называется самоприменимой. Предполагается, что машина Тьюринга универсальна, она читает код своего номера (программы), с ленты, расшифровывает его и в соответствии с ним выполняет необходимые действия в зависимости от начальной конфигурации (данных), также записанные на ленте. Машина, не применимая к слову n(M), называется несамоприменимой. Проблема самоприменимости (впервые эта проблема рассмотрена отечественным математиком О.Б. Лупановым [24]) заключается в том чтобы по заданной программе Р для абстрактной машины узнать, применима ли она к своей собственной записи Р((Р)), где (Р) – запись программы или подпрограммы n(P) [7]. Например, программа машины, заменяющей символы 1 на 0, а 0 на 1, применима к любому слову, в частности и к своей записи, если мы закодируем записи программ в двоичном коде, что вполне возможно, поэтому она самоприменима, а программа В: B: 1)?{l,2}; 2) HLT, применима только к пустому слову, т.е. несамоприменима. В машине В, если головка в начальный момент обозревает ячейку, в которой записан не пробел l, то произойдет безрезультатная остановка. Задача заключается в отыскании такого алгоритма, который определял бы для любой программы ее самоприменимость.
|
||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 389; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

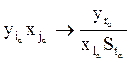 , a=1...k,
, a=1...k,