Распределение терминов в простом категорическом суждении.

Термин считается распределённым (обозначается «+»), если в данном суждении он мыслится в полном объёме, и нераспределённым (обозначается «–»), если он мыслится частью объёма (рис. 112).

S – распределён

 

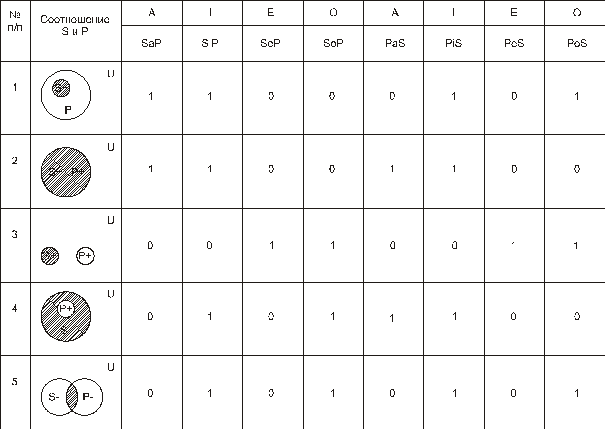
Рис. 112. Распределение терминов в суждениях

Семантика простых категорических суждений.

Семантика или смысл простых категорических суждений рассматривается на основе анализа понятий суждения с учетом всевозможных отношений между ними на некотором универсуме рассуждения. Рассмотрим суждения с их иллюстрацией (рис. 113) на кругах Эйлера [16].

1) SaP.

Например, всякий компьютер является ЭВМ

 

2) SeP.

3) SiP.

4) SoP.

Рис. 113. Суждения и соответствующие типичные случаи

отношений между понятиями

Термин распределен, если он полностью заштрихован или полностью не заштрихован, и нераспределен в противном случае (рис. 113).

Отношения между суждениями можно представить табл. 80.

Таблица 80

Отношения между суждениями

В табл. 80 обозначено: 1 – «истинно», 0 – «ложно». Здесь выделено только пять наиболее существенных соотношений S и P.

Анализ отношений между суждениями может быть проведён путём сравнения соответствующих столбцов табл. 80.

Располагая информацией об истинности или ложности одного суждения можно установить, каким будет другое суждение.

Логический квадрат.

Отношения между суждениями может быть представлено графом – логическим квадратом (рис. 114):

Рис. 114. Логический квадрат

 

На логическом квадрате указаны метки дуг, показывающие связь между понятиями. Видно, что есть однозначные связи: например, от истинности суждения Е к ложности суждения А. Неоднозначна связь, например, от ложности суждения А к истинности суждения Е.

 

УМОЗАКЛЮЧЕНИЕ

 

13.1. Виды умозаключений

 

Умозаключение – форма мысли, в которой устанавливается такая связь между суждениями, с помощью которой обеспечивается получение новых истинных суждений на основе уже имеющихся [8, 16].

Новое истинное суждение, полученное в результате умозаключения, называется выводом, при этом исходные суждения называются посылками.

Между посылками и выводом должно существовать отношение следования. Вывод следует из посылок, если истинность посылок приводит к истинности умозаключения, т.е. важно следование и важна истинность посылок.

Задача логики – сформулировать правила, обеспечивающие истинность вывода при условии истинности посылок.

Выделяют дедуктивные и индуктивные умозаключения.

Дедуктивное умозаключение («дедукция» – от лат. «выведение») – обеспечивает переход от более общих суждений к менее общим, то есть частный случай подводится под действие общего закона, правила, теоремы.

Если при построении умозаключения производится переход от истинности единичного или частного суждения к общему, то такое суждение называется индуктивным (от лат. «наведение»).

Различают полную индукцию (обобщение на основе конечной обозримой области фактов) и неполную (относится к бесконечной области фактов).

Дедуктивные умозаключения могут быть непосредственными и опосредованными.

Если истинность вывода обосновывается с помощью одной посылки, то умозаключение непосредственное. Если с помощью двух и более – опосредованное.

13.2. Непосредственное умозаключение

 

Непосредственное умозаключение строится двумя путями:

1. Путем преобразования исходного суждения (посылки).

2. На основе знаний об отношениях между суждениями.

Умозаключение путем обращения суждения.

При таком умозаключении меняются субъект и предикат исходного суждения:

S – P (посылка)

P – S (заключение)

Примеры.

1. Все предприниматели платят налоги, следовательно, некоторые плательщики являются предпринимателями.

2. Все ЭВМ являются компьютерами, следовательно, все компьютеры являются ЭВМ.

3. Некоторые студенты работают, следовательно, некоторые трудящиеся являются студентами.

4. Некоторые учащиеся – студенты, следовательно, все студенты – учащиеся.

Обращение бывает двух видов: чистое или простое (примеры 2 и 3, квантор не меняется) и с ограничениями (примеры 1 и 4, квантор меняется на противоположный).

Простое обращение – когда субъект и предикат либо оба распределены, либо оба не распределены.

С ограничением – когда субъект распределен, а предикат нет или наоборот.

Изобразим обращение суждений табл. 81.

Таблица 81

Обращение суждений

С помощью этой таблицы можно определить, когда возможно обращение – опять-таки, тогда, когда связь между суждениями однозначная.

Умозаключение путем превращения суждений.

При превращении меняется качество посылки без изменения количества, при этом предикат заключения является отрицанием предиката посылки.

S есть P	или	S есть `P
S не есть `P	S не есть P

Частноутвердительное превращается в частноотрицательное, общеутвердительное – в общеотрицательное.

Превращению могут быть подвержены все суждения.

Примеры.

1. Все женщины красивы, следовательно, ни одна женщина не является не красивой.

2. Некоторые мужчины – джентльмены, следовательно, некоторые мужчины не являются не джентльменами.

Изобразим превращение табл. 82.

Таблица 82

Превращение суждений