
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Семантика формул логики предикатовСодержание книги
Поиск на нашем сайте
Формула имеет семантику, т.е. определенный смысл, и обозначает определенное высказывание, если существует ее некоторая интерпретация. Интерпретировать формулу– значит связать с ней определенное непустое множество, т.е. конкретизировать предметную область (область интерпретации), а также указать соответствие [25]: 1) каждой предметной константе в формуле – конкретный элемент из множества М; 2) каждой n-местной функциональной букве в формуле – конкретную n-местную функцию на множестве М; 3) каждой n-местной предикатной букве – конкретное отношение между n элементами на М. Пример [25]. G2(f(a,b)), g2(a,b) Пусть М – множество натуральных чисел a=2, b=3, f – сложение (a+b), g – умножение (a×b), G – отношение «не меньше» (³). Тогда: 2+3³2×3 – ложное высказывание Если a=1, b=2 – высказывание истинное. Не существует ни одной интерпретации G, при которой эта формула и истинна и ложна одновременно. Для формулы G2(f(g(x,x),g(y,y),g(a,g(x,y))) при a=2: «x2+y2³2xy» – истинное высказывание. Общезначимость, выполнимость, невыполнимость. Формула без свободных переменных называется замкнутой. Для данной интерпретации всякая замкнутая формула представляет собой высказывание, которое истинно или ложно. А всякая формула со свободными переменными выражает некоторое отношение на области интерпретации, которое может быть истинно для одних значений переменных и ложно для других значений. Если формула истинна при всех интерпретациях, то она общезначима, например: Если формула ложна при любых интерпретациях, то она невыполнима, например: Формула выполнима, если существует интерпретация, в которой она выполнима. Логика предикатов второго порядка – логика, использующая кванторы по предикатным буквам и (или) по функциям. Предикаты в информатике могут задаваться и в «неакадемической» форме – с использованием слов естественного языка, например: находиться <Иван, работа> – двухместный предикат «Находиться <Х,У>» – Х находится в У.
ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ ФОРМУЛ ЛОГИКИ ПРЕДИКАТОВ
Операции над предикатами
Над предикатами можно производить обычные логические операции [24]. В результате получают новые предикаты. Инверсией предиката называется предикат, у которого значения истинности проинверсированы. Конъюнкцией предикатов называется предикат, у которого множество истинностей является пересечением множеств истинности исходных предикатов. Пусть Р(х) означает предикат «х делится на 2», Q(x) означает предикат «х делится на 3», P(x)∙Q(x) означает предикат «х делится на 2 и х делится на 3», т.е. определяет предикат делимости на 6. Дизъюнкцией предикатов называется предикат, у которого множество истинности является объединением множеств истинности исходных предикатов. Аналогично могут быть определены эквиваленция и импликация. Очевидно, что переменные должны принимать значения из одного общего множества. Пусть предикаты P1(x,y) и P2(x,y) (X={c,d,e},Y={a,b,c,d}) определяются соответствующими таблицами (табл. 85-86) [24]: Таблица 85 Для P1(x,y)
Таблица 86 Для P2(x,y)
Тогда импликацией P1(x,y)→P2(x,y) будет предикат Ри(х,у) (табл. 87), ложный в соответствующих клетках (табл. 85-86), где первый предикат P1(x,y) истинный, а P2(x,y) – ложный. Эквиваленцией P1(x,y)↔P2(x,y) будет предикат Pэ(x,y) (табл. 88), истинный в соответствующих клетках (табл. 85-86), где оба предиката принимают одинаковые значения. Таблица 87 Для Pи(x,y)
Таблица 88 Для Pэ(x,y)
Также, как в логике высказываний определяется равносильность предикатов – она выполняется, когда на всяком наборе значений входящих в них переменных предикаты принимают одинаковые значения: P1(x,y)«P2(x,y). Таким же образом можно определить следование P1(x,y)→P2(x,y) предиката P2 из предиката P1. Это выполняется тогда, когда P1(x,y)→P2(x,y) истинно на всех наборах переменных, т.е. множество истинности P1 является подмножеством множества истинности предиката P2 (множество предиката P1 включается во множество истинности предиката P2). Очевидно, что свойства – одноместные отношения – являются одноместными предикатами, а многоместные отношения – это многоместные предикаты.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 420; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

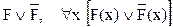 .
.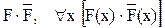 .
.


