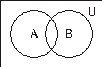Представление схемы алгоритма микропрограммой

С двумя типами микрокоманд

 

Дальнейшее углубление в область программного обеспечения заключается в сопоставлении каждому блоку ГСА некоторой микрокоманды, которая, в простейшем случае формируется из микрокоманд двух типов [31]: 1) операционной (рис. 101) и 2) специальной или перехода (рис. 102).

 

Признак микрокоманды ПМ=1

Микрооперации

 

Рис. 101. Операционная микрокоманда: ПМ=1

 

Признак микрокоманды ПМ=0

Код логического условия

Адрес перехода

 

Рис. 102. Специальная, или переходов: ПМ=0

 

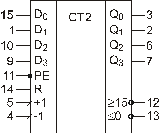
Если выполняется операционная микрокоманда, то последовательно выбираются адреса постоянного запоминающего устройства (ПЗУ) и последовательно выдаются микрооперации в операционное устройство. Это может быть реализовано путем перебора состояний счетчика по счетному входу +1 (рис. 103).

Рис. 103. Условное графическое обозначение счетчика

со счетным входом +1

Такой счетчик будет называться счетчиком микрокоманд. Конечно, для задач реальной размерности он должен иметь достаточное число состояний в отличие от счетчика, изображенного на рис. 103.

В случае выполнения специальной микрокоманды (рис. 102), если логическое условие равно единице, – производится переход по указанному адресу с использованием входа предустановки РЕ по указанным в поле адреса данным D_i. Если логическое условие равно нулю, то выбирается следующий адрес. Если номер логического условия равен нулю, то это безусловный переход, и производится передача управления по указанному адресу (на входах D_i).

Такая логика управления реализуется блоком управления – счетчик микрокоманд, который адресует память микропрограмм.

Получим микропрограмму реализации алгоритма, изображенного на рис. 98 для автомата с двумя типами микрокоманд (табл. 77).

 

Таблица 77

Микропрограмма с двумя типами микрокоманд

Метка

Адрес микрокоманды

Микрокоманда

Комментарий

ПМ

M0:

Переход, если х1=1 на адрес 1100

Переход, если х2=1 к блоку 3 ГСА по адресу 0111 (метка М2)

Выдача z4=1 (A4)

Возврат в 0000 безусловно к метке М0

-

-

-

-

-

-

-

-

Не используется

-

-

-

-

-

-

-

-

Не используется

-

-

-

-

-

-

-

-

Не используется

M2:

Выдача z1=1 (A1)

Выдача z2,z3=1 (A2)

M3:

Ожидание х3=1. Переход к метке М4, если х3=1

Если х3=0, то АÆ и безусловный переход к проверке х3 (метка М3)

-

-

-

-

-

-

-

-

Не используется

M1:

z4=1 (А4)

Безусловный переход на начало к метке М0

M4:

z5=1 (А3)

Безусловный переход на начало к метке М0

 

Таким образом, из табл. 77 следует, что необходимо всего 12 ячеек памяти по 8 бит, то есть всего 96 бит.

В рассмотренном автомате, если микрокоманда специальная (ПМ=0), разряды 1-2 используются для кодирования логического условия (значения указаны курсивом): 00 – безусловный переход, т.е. нет условия; 01 – х₁; 10 – х₂; 11 – х₃. Если микрокоманда операционная, то разряды 1-5 отводятся для микроопераций z₁-z₅ соответственно. Особенность микропрограммы – возврат в исходное состояние после окончания работы.

 

ЭЛЕМЕНТЫ ФОРМАЛЬНОЙ ЛОГИКИ

 

Предмет формальной логики

 

Греческое слово «логос» означает разум, рассуждение.

Согласно словарю С.И. Ожегова логика – наука о законах мышления и его формах, а также ход рассуждений и умозаключений [27].

Формальная логика имеет своим объектом рациональный уровень мышления, изучает формы мысли, а не её содержание.

Главная цель формальной логики состоит в том, чтобы разработать такие правила оперирования формальными структурами, которые бы обеспечивали последовательность, правильность и доказуемость мышления, истинность рассуждений [8].

Мышление – процесс получения, хранения и переработки информации, целью и результатом которого является получение идеального образа изучаемого объекта.

Различают чувственное и рациональное мышление.

Человек получает информацию с помощью органов чувств. Можно рассматривать следующие формы отражения действительности в чувственном мышлении:

· ощущения – отражение в сознании отдельных сторон объективной реальности;

· восприятие – отдельные свойства объективной реальности, объединённые в комплексы ощущений. В процессе восприятия формируется идеальный образ объекта;

· представление – форма отражения действительности, когда объект не вызывает непосредственного воздействия на сознание.

Переход от единичных объектов к классам объектов осуществляется путем обобщения .

Основные формы рационального мышления (объекты формальной логики):

· понятие – отражение наиболее общих существенных признаков и свойств реальных объектов;

· суждение – установление связи между понятиями, утверждение или отрицание наличия связи между предметами, признаками и свойствами;

· умозаключение – фиксирует связи между суждениями и отношения между ними. Умозаключение обеспечивает переход от одних истинных суждений к другим новым истинным суждениям.

Логический подход изучает лишь форму, структуру мысли, отвлекаясь от содержания. Особенно важно отношение логического следования.

Открытие, изучение и систематизация правил, позволяющих из принятых истинных суждений выводить новые истинные суждения – является главной задачей логики.

История логики.

Логика как наука сформировалась очень давно – в IV веке до н.э. Ее создал древнегреческий ученый Аристотель. В течение многих веков логика почти не развивалась. Это, конечно, свидетельствует о гениальности Аристотеля, однако в свое время логика приобрела славу мертвой, застывшей науки и высмеивалась Рабле, Свифтом и др. [25].

Основное содержание логики Аристотеля – теория дедуктивных рассуждений. Дедукция – умозаключение, позволяющее осуществить переход от общего суждения к частному. Другое название этого раздела логики – силлогистика. Сейчас эту логику называют формальной.

Индукция – мышление, позволяющее осуществить переход от частного решения к общему. Основатели: Рожер Бэкон, Френсис Бэкон.

Только в ХVП веке великий немецкий ученый Лейбниц (1646-1716 гг.) задумал усовершенствовать, математизировать логику, которая стала бы «искусством исчисления». В этой логике, по мысли Лейбница, каждому понятию соответствовал бы символ, а рассуждения имели бы вид вычислений. Для этой цели Лейбниц использовал простые числа. Идея Лейбница, не встретив понимания современников, не получила в то время распространения и развития [25].

В середине ХIХ века ирландский математик и священник Дж. Буль (1815-1864 гг.) частично воплотил в жизнь идею Лейбница. Им была создана алгебра логики, в которой действуют законы, схожие с законами традиционной алгебры, но буквами обозначаются не числа, а предложения. На языке такой алгебры (булевой алгебры логики) можно описывать рассуждения и «вычислять» их результаты; однако ею охватываются далеко не всякие рассуждения, а лишь определенный их тип, в некотором смысле – простейший. Это знаменовало начало становления математической логики [25].

В 20-30-ые годы прошлого века от классической логики переходят к неклассической логике. Формальная логика – ядро научного мышления, элемент общей научной культуры [8, 16]. Большой вклад в развитие математической логики внесли ученые разных стран: Д. Гильберт (1862-1943 гг.), Б. Рассел (1872-1970 гг.), К. Гёдель (род. в 1906 г.), А.Н. Колмогоров (1903-1987 гг.), Я. Лукасевич (1878-1956 гг.), А. Тарский (1901-1983 гг.), А. Черч (род. в 1903 г.), А. Тьюринг (1912-1954 гг.), А.А. Марков (1903-1980 гг.) и др.

 

Понятие и его виды

 

Понятие – это абстрактный образ класса сходных объектов, в котором фиксируются наиболее общие свойства и признаки.

При формировании понятий используются методы обработки информации: анализ, синтез, сравнение, обобщение, абстрагирование, идеализация. В результате формируются идеальные образы – понятия. Понятие непосредственно связано со словом.

Связь объект-понятие возникает не сразу. Понятие двойственно (слово и объект) [8]. Понятием могут быть имена существительные и другие части речи.

Содержание понятия – совокупность тех свойств и признаков, которые были выделены в качестве основных в процессе образования понятий.

Объем понятия – это мыслимая совокупность элементов, выступающих носителем свойств и признаков.

Изменяя содержание понятия, мы влияем на его объем. Увеличивая число признаков, объем понятия сокращается. Эта связь фиксируется в логике законом обратного соотношения между содержанием и объемом понятия.

Виды понятий.

Понятия классифицируются по объему:

· единичные – одноэлементный класс («Президент России В.В. Путин»);

· общие – класс, содержащий более одного элемента. Среди общих выделяют понятия, являющиеся универсумом;

· пустые – класс, соответствующий пустому множеству («Король России»).

Понятия классифицируются по содержанию:

· конкретные – задают некоторый класс материальных или идеальных объектов;

· абстрактные – отражают некоторые свойства и признаки материальных или идеальных объектов в отрыве от их носителей, которые становятся некими самостоятельными сущностями (честность, храбрость);

· относительные – понятия, в которых мыслятся предметы, существование которых предполагает наличие других предметов («обучаемый» – «обучающий»);

· безотносительные («математика», «дом»);

· положительные – характеризуют наличие некоторого свойства («живущий по средствам»);

· отрицательные – в которых признаки положительных понятий отрицаются («живущий не по средствам»);

· собирательные – группа однородных предметов, мыслимое как единое целое («созвездие»);

· несобирательные – можно отнести к отдельному предмету. Несобирательные понятия называют разделенными.

 

Отношения между понятиями

Если в содержании некоторых понятий имеются общие признаки, то они совместные, иначе несовместные [8, 16].

Отношения между понятиями могут быть изображены диаграммами Эйлера, на которых вместо множеств рисуют понятия на некотором универсуме рассуждения U.

Между совместными понятиями складываются следующие отношения.

Совпаденияилитождества (рис. 104).

Рис. 104. Совпадение понятий А, В

Включенияилиподчинения (рис. 105).

Рис. 105. Понятие A включается в объем понятия B

 

В – родовое понятие, А – видовое понятие.

Пересечения (рис. 106).

 

Рис. 106. Понятие A пересекается с понятием B

 

Между несовместными понятиями складываются следующие отношения.

Соподчинения или координации (рис. 107).

Рис. 107. Понятия A и B соподчинены понятию С

 

Исключения или контрарности (рис. 108).

Рис. 108. Контрарность понятий A и B

Противоречия или контрадикторности (рис. 109).

Рис. 109. Противоречие понятий A и B

 

Над объёмами понятий возможно проведение булевых операций подобных операциям над множествами.

 

Операции над понятиями