
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исключение кванторов общности.Содержание книги
Поиск на нашем сайте
После исключения кванторов общности и стандартизации переменных формула содержит только кванторы общности, каждый из которых имеет свою переменную. Поэтому кванторы общности можно перенести в начало формулы (получаем предварённую формулу) и считать областью действия каждого квантора часть формулы, расположенную за ними. Например:
В связи с тем, что в импликации Таким образом, кванторы исключают, получив предваренную форму из одних кванторов общности. Представление формулы в КНФ. Получение множества Ф1 (объединение формул Пример. Исключим знаки импликации:
Уменьшим области действия знаков отрицания до одного предиката:
Произведем стандартизацию переменных:
Проведем сколемизацию:
Здесь g(z) – функция Сколема, зависящая только от x, она находится в области действия квантора. Получим предваренную форму формулы:
Исключим кванторы общности:
Используя закон дистрибутивности, получим КНФ:
Универсум Эрбрана
Полученная КНФ – это то множество формул Очевидно, что невозможно перечислить все возможные области интерпретации. Во-первых, множества могут оказаться бесконечными и, во-вторых, неясно, как их строить. Метод решения этой проблемы основывается на утверждении: если множество Ф1 невыполнимо в области Н(Ф1), называемой универсумом Эрбрана, то оно невыполнимо в любой области [29, 32]. Универсум Эрбрана Н(Ф1) для множества предложений Ф1 определяется следующим образом: · множество всех предметных констант упомянутых в Ф1 принадлежат Н(Ф1); · если некоторые термы принадлежат Ф1, то и функции от этих термов принадлежат Н(Ф1); · никакие другие термы не принадлежат универсуму Эрбрана. Пример. Тогда: Н(Ф1)={a,b,f(a),f(b),g(a,a),g(b,b),g(a,b),g(b,a),f(f(a)),f(f(b)),g(a,f(a)),…}. Множество константных частных случаев, получающихся в результате подстановки вместо переменных в Ф1 множеств из Н(Ф1) называется Эрбрановским базисом для Ф1. Множество невыполнимо на Н(Ф1), если любая интерпретирующий на Н(Ф1) не удовлетворяет Ф1. Задание интерпретаций на Н(Ф) удобно делать с использованием семантического дерева. Каждый путь в нем – одна из интерпретаций на Н(Ф). Последовательность меток для каждого пути семантического дерева – модель для данного множества предложений Ф. Каждая модель – определенная интерпретация. Модель не удовлетворяет предложению, если существует константный частный случай этого предложения, имеющий значение «0». Рассмотрим пример, включающий три предиката, описывающих свойство транзитивности:
Здесь
где Тогда фундаментальная конкретизация имеет вид:
Таким образом, имеется всего 8(23) Эрбрановых интерпретаций. Соответствующее семантическое дерево имеет вид (рис. 118):
Рис. 118. Семантическое дерево
В соответствии с рис. 118 – по всем возможным путям из корня к листьям дерева можно получить все 8 вариантов фундаментальной конкретизации:
Таким образом, при всех вариантах получаем невыполнимое множество дизъюнктов. В ряде случаев нет необходимости опускаться до листьев, например, если Пример [32]. Схема индукции.
В базис индукции: «а» – некоторое конкретное значение из множества натуральных чисел; f – функция определения следующего натурального числа (N);
Эрбранова область H(Ф)={a, b, f(a), f(b), f(f(a))…f(n)(a), f(n)(b)…}, где f(n) – композиция n-го порядка, т.е. имеется бесконечное число Эрбрановых интерпретаций. Каждая из них сопоставляет некоторое значение истинности каждому элементу бесконечного множества. H(Ф)={P(a),P(b),P(f(a)),P(f(b)),P(f(f(a)))…}. Существование некоторой истинной интерпретации достаточно для доказательства выполнимости множества Пусть P(f(n)(a))=1, P(f(n)(b))=0 для всех n. Тогда (рис. 119):
Рис. 119. Семантическое дерево
Получаем Т.е. схема индукции верна не для всех интерпретаций! Верно только для xÎN, f=x+1, а соответствующая формула – не общезначима.
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 405; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.144.162 (0.006 с.) |

 .
.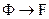 множество состоит из замкнутых формул, т.е. из формул, не содержащих свободных переменных, и формула F замкнута, все переменные в формуле из
множество состоит из замкнутых формул, т.е. из формул, не содержащих свободных переменных, и формула F замкнута, все переменные в формуле из  будут относиться к кванторам общности. А так как порядок расположения кванторов общности не имеет значения, то эти кванторы можно явно не исключать, условившись, что все переменные в формуле относятся к кванторам общности.
будут относиться к кванторам общности. А так как порядок расположения кванторов общности не имеет значения, то эти кванторы можно явно не исключать, условившись, что все переменные в формуле относятся к кванторам общности. ) эквивалентно КНФ соответствующей формулы. Так как какая-либо интерпретация удовлетворяет формуле вида
) эквивалентно КНФ соответствующей формулы. Так как какая-либо интерпретация удовлетворяет формуле вида  в том и только в том случае, если она удовлетворяет формулам и К1, К2, …, Кn одновременно, то исходную формулу Ф1 можно заменить множеством конъюнктивных членов (дизъюнктов).
в том и только в том случае, если она удовлетворяет формулам и К1, К2, …, Кn одновременно, то исходную формулу Ф1 можно заменить множеством конъюнктивных членов (дизъюнктов). .
. .
. .
.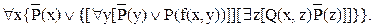

 .
. .
.

 .
. , невыполнимость которого нужно доказать – доказать, что не существует интерпретации, которая ему удовлетворяет.
, невыполнимость которого нужно доказать – доказать, что не существует интерпретации, которая ему удовлетворяет. .
.
 гипотезы, а C – заключение соответствующего умозаключения. В этом случае клаузальная форма имеет вид:
гипотезы, а C – заключение соответствующего умозаключения. В этом случае клаузальная форма имеет вид:
 – отрицание заключения
– отрицание заключения  , «а» – функция Сколема.
, «а» – функция Сколема.




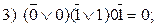




 равны нулю, ясно, что сразу получаем нуль. Это указывается на дереве специальным кружком.
равны нулю, ясно, что сразу получаем нуль. Это указывается на дереве специальным кружком.
 .
.


 , n,mÎN.
, n,mÎN. .
.


