
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Использование метода резолюций
В ЛОГИКЕ ПРЕДИКАТОВ
Подстановка и унификация
В математической логике широко используются приемы подстановки и унификации. Подстановка – приём, в результате которого из некоторых данных формул получают их частные случаи, например, {(t1,x1),…,(tn,xn)}, где пара (tj,xi) означает, что всюду, где производится данная подстановка, переменная xi заменяется термом tj. Пример [29]. Литерал Р(х,f(y),b) после подстановок: q1={(z,x), (w,y)}; q2={(a,y)}; q3={(g(z),x), (a,y)} имеет вид: Pq1=P(z,f(w),b); Pq2=P(x,f(a),b); Pq3=P(g(z),f(a),b). Здесь Pqi означает частный случай Р, полученный при подстановке qi. Композиция двух подстановок qi и qj. Композиция подстановок qiqj получается при применении подстановки qj к термам подстановки qi, с последующим добавлением любых пар из qj, содержащих переменные, не входящие в число переменных из qi[29]. Например: qi={(f(x),z)} и qj={(a,x),(b,y),(d,z)}, то qiqj={(f(а),z),(b,y)}. Нетрудно убедиться, что применение к литералу последовательно подстановок qi и qjдаёт тот же результат, что и применение подстановки qiqj: Композиция подстановок ассоциативна: (qiqj)qk=qi(qjqk). Унификация. Множество литералов {Li} называется унифицированным, если существует такая подстановка q, что L1q=L2q=,…=Lnq; Подстановка q называется унификатором для {Li}. Унификация применяется и для формул. Формулы, имеющие совместный частный случай, называются унифицируемыми, а набор подстановок – общим унификатором. Наименьший возможный унификатор называется наиболее общим унификатором. Известен алгоритм унификации, определяющий, являются ли две заданные формулы унифицируемыми, и, если это так, то позволяющий найти наиболее общий унификатор. Заметим, что при подстановке переменная заменяется термом, но терм не может быть заменен термом! Т.е., вместо переменной может быть подставлена константа, другая переменная, функция, но вместо константы или функции ничего не может быть подставлено!
Резольвенция и факторизация При доказательстве теорем в математической логике используются представления суждений в виде дизъюнкции литералов (в виде предложений, в клаузальной форме). Литерал L1 называется дополнительным литералу L2, если L1 является отрицанием L2. Резольвента двух предложений получается следующим образом [29]: 1) переменные одного предложения переименовываются таким образом, чтобы они отличались от переменных другого предложения;
2) находится подстановка, при которой какой-либо литерал одного предложения становится дополнительным к какому-либо литералу другого предложения и эта подстановка производится в оба предложения; 3) литералы, дополнительные друг к другу, вычёркиваются; 4) если имеются одинаковые литералы, то все они, кроме одного в каком-либо предложении вычёркиваются; 5) дизъюнкция литералов, оставшихся в обоих предложениях, и есть резольвента. Используется также факторизация. Фактором какого-либо предложения называется следствие этого предложения [29]: 1) находится подстановка при которой какие-либо литералы одинаковы; 2) после выполнения этой подстановки все одинаковые литералы, кроме одного, вычёркиваются; 3) дизъюнкция оставшихся литералов и есть фактор. Процесс нахождения фактора называется факторизацией. Пример [29].
Резольвента
Здесь резольвенты нет. Переменные: x, y – термы: g(x), f(x). Вместо переменной можно подставить терм, но вместо функции или константы терм подставить нельзя! Пример [26]. {P(x,a,f(g(a))),P(z,y,f(u))}. В этом случае наименьший общий унификатор: {(z,x),(a,y),(g(a),u)}. Просто унификатор: {(b,x),(a,y),(b,z),(g(a),u)}.
|
|||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 311; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.168.28 (0.005 с.) |
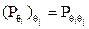 .
. .
.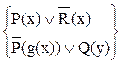
 при подстановке {(g(x),x}, то есть g(x) заменяет x.
при подстановке {(g(x),x}, то есть g(x) заменяет x.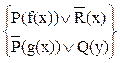 .
.


