
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условно-разделительный силлогизм: одна из посылок – условное суждение, А другая – разделительное суждение.Содержание книги
Поиск на нашем сайте
В зависимости от числа альтернатив различают: · дилемму – 2 альтернативы; · трилемму – 3 альтернативы; · тетралемму – 4 альтернативы. Конструктивная дилемма:
Совокупность произвольных посылок и произвольных заключений называется аргументом. Проверка правильности аргументов – это проверка следования из конъюнкции посылок заключения. Получение следствий из данных посылок
Получение следствий из данных посылок можно осуществить, получив СКНФ данных посылок, тогда все возможные сочетания элементарных конъюнкций и будут всевозможными следствиями из данных посылок. Например:
Следствия данных посылок:
Нужно получить СКНФ и перебрать все возможные комбинации конъюнкций (в данном случае у нас, их 7), т.е. получается булеан от членов СКНФ без одного элемента (пустого множества).
Метод резолюций
Если имеются два высказывания:
Такие следствия называются резольвентами (это дизъюнкция членов при контрарных литералах). Метод основан на получении резольвент. Последовательно получаем резольвенты исходного множества формул, доказательство невыполнимости которого мы ведем, до тех пор, пока не получится Æ (пустое следствие). Здесь доказательство ведется от противного. Для применения этого метода необходимо использовать КНФ. Например, для modus ponens:
Получили дерево доказательства. Взяты две посылки и отрицание заключения в КНФ. Следствием посылок
СИНТАКСИС И СЕМАНТИКА ЯЗЫКА ЛОГИКИ ПРЕДИКАТОВ Понятие предиката
Предикат (от лат. «сказуемое») Р(x1,x2,...,xn) – функция, переменные которой принимают значения из некоторого произвольного множества М или множеств, возможно и бесконечных, а сама функция принимает 2 значения: «истина» или «ложь». Р(x1,x2,...,xn):Mn То есть, предикат – это отображение n-ой степени произвольного множества в бинарное множество В, элементы которого принимают два значения: «истина» или «ложь». Переменные называются предметными или пропозициональными. Таким образом, понятие предиката является расширением понятия логическая функция. Предикат от n переменных называется n-местным предикатом. Вместо предметных переменных в предикат могут быть подставлены определенные значения из предметной области М, т.е. константы. Также в предикат могут быть подставлены некоторые n-местные функции: f(x1,x2,...,xn):Mn Очевидно, что высказывание – нульместный предикат, свойство – одноместный предикат, n-местное отношение – n-местный предикат. Предикат на конечных множествах может быть задан соответствующей таблицей (табл. 84) [24]. Пример. P(x,y) «x<y» Мх={1,2,3} Му={2,4} Мх×Му Таблица 84 Предикат на конечных множествах
Множество истинности данного предиката – множество, в котором предикат принимает значение «1».
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 296; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.254.35 (0.006 с.) |




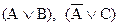 которые имеют контрарные или инверсные (
которые имеют контрарные или инверсные ( ) литералы, то следствием из этих посылок является (BÚC). Проверим это утверждение:
) литералы, то следствием из этих посылок является (BÚC). Проверим это утверждение:
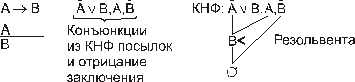
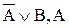 является резольвента B, а следствием
является резольвента B, а следствием 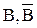 является пустое множество Æ. Это признак невыполнимости исходного множества членов КНФ. А т.к. доказательство проводилось от противного, стало быть, мы и доказали следование B из посылок A®B,A.
является пустое множество Æ. Это признак невыполнимости исходного множества членов КНФ. А т.к. доказательство проводилось от противного, стало быть, мы и доказали следование B из посылок A®B,A.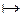 B, B:{0,1}.
B, B:{0,1}.


