
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формы представления формул логики высказыванийСодержание книги
Поиск на нашем сайте
Скобочная форма, образуется непосредственно после формализации высказывания. Дизъюнктивная нормальная форма – дизъюнкция элементарных конъюнкций. Конъюнктивная нормальная форма – конъюнкция элементарных дизъюнкций. КНФ также называют клаузальной формой. Клауза – элементарная дизъюнкция. Литера, литерал – элементарное высказывание или его отрицание. Дизъюнкт – дизъюнкция конечного числа литералов. Хорновский дизъюнкт имеет не более одной не инверсной литеры. Пример.
Хорновские дизъюнкты используются в языке ПРОЛОГ (PROLOG, от PROgramming in LOGic – программирование в логике; разработан в 1972 г. Аланом Колмари) для описания правил типа «Если, то». Кстати, в ПРОЛОГЕ с помощью импликации записываются и так называемые факты:
Т.е. факт – это утверждение истинности некой формулы. Преобразование в КНФ обычно производится при помощи распределительного закона. СКНФ получают из КНФ путём добавления к каждому дизъюнкту тождественно ложной литеры.
Проблема дедукции в логике высказываний Помимо равносильности в логике широко используется отношение следования. Говорят, что формула S является следствием множества формул H (записывается так: H├S) если при всех интерпретациях, при которых истинны все формулы из H, истинна также и формула S [32]. Таким образом, тавтология – следствие из пустого множества формул. Записывается так: ├T, т.е. слева от знака ├ нет символа, но он подразумевается равным константе 0, – как в факте. S является следствием из H тогда и только тогда, когда их импликация истинна H→S≡1: (H├S)↔[(H→S)≡1]; ├(H→S). Если рассматривается множество формул или гипотез H1,H2,…,Hn, то (H1,H2,…,Hn)├S↔├(H1×H2×…×Hn)→S – т.е. подразумевается импликация из конъюнкций этих формул, которая общезначима. Таким образом, из множества формул выводима формула S (├S). Фундаментальная проблема логики: определить является ли S следствием из множества формул H (проблема дедукции). Проблема описывается так: необходимо установить общезначимость следования H→S. Доказательство может быть проведено следующим образом:
или, наоборот, путем доказательства невыполнимости:
Во втором случае говорят, что доказывают невыполнимости объединения формулы H и формулы S.
ПРОВЕРКА ПРАВИЛЬНОСТИ ЛОГИЧЕСКИХ ВЫВОДОВ. МЕТОД РЕЗОЛЮЦИЙ
Закон контрапозиции
На основе данного сложного высказывания А®В можно сформулировать обратное ему высказывание B®A. Нетрудно убедиться, что оно не равносильно исходному. Для всякого сложного высказывания A®B можно сформулировать противоположное Высказывание типа Нетрудно убедиться, что оно равносильно исходному:
Такая равносильность называется законом контрапозиции [25]. Согласно этому закону: 1) высказывания A®B и 2) высказывание, которое является обратно противоположной данной теореме A®B также является теоремой (здесь сложное высказывание называется теоремой); 3) вместо данной теоремы можно доказать обратно противоположную ей теорему. Кроме того, если высказывание A®B – теорема, то A есть достаточное условие B, а B – необходимое условие A. Если оба высказывания являются теоремами (A®B, B®A; т.е. A«B), то A – необходимое и достаточное условие B, а B – необходимое и достаточное условие A. Если A®B – теорема, а B®A не теорема, то A – достаточное, но не необходимое условие B, а B – необходимое, но не достаточное условие A.
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 294; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.183.187 (0.006 с.) |

 .
. .
.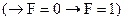 .
. ,
, .
. . Нетрудно убедиться, что оно не равносильно исходному.
. Нетрудно убедиться, что оно не равносильно исходному. называется обратно – противоположным.
называется обратно – противоположным. .
. одновременно истинны либо одновременно ложны;
одновременно истинны либо одновременно ложны;


