
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Семантика логики высказыванийСодержание книги
Поиск на нашем сайте
Если в формальной логике суждения расчленяются на субъект и предикат, то в логике высказываний суждение не расчленяется, а рассматривается как простое, из которого с помощью логических операций строится сложное суждение. С логики высказываний и началась собственно математическая логика. В логике высказываний используется понятие «Высказывание». Высказывание – это предложение, которое либо истинно, либо ложно. Высказывание – как правило, повествовательное предложение. Если нет общего мнения об истинности, то это не является высказыванием. Из двух и более высказываний строятся сложные высказывания, с помощью логических операций, рассмотренных ранее (см. «Переключательные функции и способы их задания»): 1) Конъюнкция: (логическое «И», «логическое умножение»). Обозначения: ×, Ù, &, AND. 2) Дизъюнкция (логическое «ИЛИ», «логическое сложение»). Обозначения: Ú, OR. 3) Импликация («если…, то», «тогда, когда»). Обозначения: ®, Þ, É, IF – THEN. 4) Эквиваленция (логическое «тогда и только тогда, когда»). Обозначения: «, Û, EQV. 5) Разделительное «или» (неравнозначность или «сумма по модулю 2», или «исключающее или»). Обозначение: Å, XOR. 6) Инверсия (логическое «НЕ», «неверно, что»). Унарная операция. Обозначения: `, Ø, NOT. Особое внимание в логике уделяется импликации, левый член называется антецедент, а правый – консеквент: X®Y=`XÚY. В логике высказываний переменные обозначаются прописными буквами. «Штрих Шеффера» и «Стрелка Пирса» – бинарные операции, с помощью которых могут быть выражены все другие операции. Штрих Шеффера (логическое «И-НЕ»). Обозначение: |, A|B= Стрелка Пирса (логическое «ИЛИ-НЕ»). Обозначение: ¯, А¯В= Символы логических операций называются пропозициональными знаками, а символы переменных – пропозициональными переменными. В основании математической логики лежат законы Аристотеля. Они уже нам знакомы. I закон – тождества. В процессе определенного рассуждения каждое понятие и суждение должно быть тождественно само себе. Х≡Х или Х®Х. II закон – противоречия. Невозможно, что одно и то же, в одно и то же время, было и не было присуще одному и тому же в одном и том же отношении.
III закон – исключенного третьего. Равным образом не может быть ничего промежуточного между двумя членами противоречия, а относительно чего-то одного необходимо, чтобы то ни было, либо утверждать, либо отрицать.
Часть логиков считают, что в ситуациях относительных к будущему закон исключенного третьего не применим. Но это уже неклассическая логика.
|
||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 475; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.008 с.) |

 .
.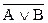 .
. (ложно),
(ложно), 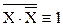 (истина).
(истина). (истина).
(истина).


