Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы теории нечетких множеств и нечеткая логикаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Нечёткая логика («fuzzy logic», расплывчатая, размытая, «пушистая логика») использует лингвистическую неопределенность и основана на теории нечетких множеств [29]. Впервые была предложена профессором компьютерных наук университета г. Беркли (США) Л. Заде в середине 60-х годов ХХ века. Обычное «четкое» множество имеет четкие границы в некотором универсуме. Принадлежность элемента универсума к некоторому множеству оценивается бинарно: «Да» или «Нет». Такая принадлежность элемента х к множеству А на универсуме U может быть описана так называемой функцией принадлежности mА: А={(х, mА(х))},хÎU, mА(х)Î{0,1}. Здесь А задано как совокупность пар – «элемент-степень принадлежности к множеству». То есть для обычного множества mА это отображение элементов универсума U в бинарное множество {0,1}:mА:Ua{0,1}. Нечёткое множество А в универсуме (пространстве) U задается функцией принадлежности, отображающей универсум не в бинарное множество, а в интервал [0,1]. Тогда задание нечеткого множества выглядит так: А={(х,mА(х))},хÎU,mА(х)Î[0,1],mА:Ua[0,1]. То есть, степень принадлежности элемента к множеству оценивается не скачком «либо 0, либо 1», а плавно, например: 0;0,1;0,4;0,7;0,9;1. Функция принадлежности может задаваться формулой, графически – например так, как указано на рис. 128.
Рис. 128. Функции принадлежности а) дискретная, б) плавная-кусочно-линейная, в) сигмоида
В случае конечного обозримого множества применяют следующую запись [41]:
Это означает, что: · элемент 1 принадлежит к универсуму U со степенью 0, т.е. не принадлежит; · элемент 2 принадлежит к универсуму U со степенью 0,1; · элемент 3 принадлежит к универсуму U со степенью 0,3; · элемент 4 принадлежит к универсуму U со степенью 0,5; · элемент 5 принадлежит к универсуму U со степенью 0,8. Знак + означает объединение элементов. Сам универсум U=1+2+3+4+5. Множество пусто, если "xÎU mА(х)=0, т.е. А=Æ. Если "xÎU mА(х)=1, то А=U. Два множества А и В равны, если mА=mВ, т.е. А=В. Множество А включается в В, если mА£mВ т.е. АÍВ. Множество `A есть дополнение множества А, если Вводятся также двухместные теоретико-множественные операции: Пересечение множеств А и В: АIВ=mАIВ = min{mА;mВ }. Пример.
Объединение множеств АUВ=mАÈВ=max{mА;mВ}. Пример.
Этим операциям соответствуют нечеткие конъюнкция и дизъюнкция в нечеткой логике, где А и В – элементарные нечеткие высказывания, а АÚВ – нечеткое составное высказывание «А или В», АÙВ нечеткое составное высказывание «А и В». Тогда U – область рассуждения. Импликация в том виде, который используется в классической логике, не применяется. Чаще всего используют импликацию в виде: «Если А, то В, иначе С», при этом такое высказывание определяют через нечеткое отношение на декартовом произведении множеств, то есть Пусть Х=1+2; Y=1+2; Тогда Таблица 97 Декартово произведение нечетких множеств А и В
Получим Тогда Таблица 98 Декартово произведение нечетких множеств `A и Y
Очевидно, что универсум В таком случае То есть в данном случае получили В теории нечетких множеств также вводится операция концентрации: Con(А) – возводит функцию принадлежности в квадрат. Деконцентрация (растяжение) Dil(А) – извлекает квадратный корень из функции принадлежности. Пример. А= B= Например, если А – «маленький», то Con(А)=«очень маленький». Если В «хороший», то Dil(В)=«более или менее хороший». Вводятся также и алгебраические операции над нечеткими множествами: 1) алгебраическое произведение: 2) алгебраическая сумма: Рассмотрим пример применения нечеткой логики. Пусть нечеткие множества заданы графически на числовой (денежной) оси. Пусть П – нечеткое подмножество универсума Х «Прибыль», З – нечеткое подмножество универсума У «Зарплата». Рассмотрим три подмножества прибыли – малая (Мп), средняя (Сп), высокая (Вп); три нечетких подмножества зарплаты – малая (Мз), средняя (Сз), высокая (Вз) (рис. 129).
Рис. 129. П – нечеткие подмножества прибыли; З – нечеткие подмножества зарплаты
Пусть дано нечеткое высказывание «Какая прибыль, такая и зарплата». Очевидно, что это не одно и то же с высказыванием «Какая зарплата, такая и прибыль». В отличие от «четкой» логики, где имеет место высказывание «Прибыль тогда и только тогда, когда зарплата» (эквиваленция П«З), задается матрица нечеткого отношения R на декартовом произведении соответствующих множеств П, З: П×З=R. Получим табл. 99. В ней степени принадлежности выбраны, например, путем опроса специалистов – экспертов. Таблица 99 Матрица нечеткого отношения «Какая прибыль, такая и зарплата»
Пусть предприятием получена некоторая прибыль точка N на оси прибыли (рис. 129), которая может быть представлена выражением:
Мы провели фаззификацию – по конкретному значению прибыли N получили нечеткое множество П, показанное на рис. 129 штриховкой по оси прибыли. Спрашивается, какая будет зарплата? Зарплата З определяется как произведение нечеткого множества П на матрицу отношения R:
Полученный результат графически (штриховкой) представлен на рис. 129 (ось З). Это нечеткая зарплата, нечеткое множество З. Но мы хотим четкую зарплату! Поэтому проводят так называемую дефаззификацию, т.е. получение четкого значения параметра. Одним из способов дефаззификации является определение «центра тяжести» нечеткого множества (показанного на рис. 129 штриховкой). Таким образом, получаем довольно неплохую зарплату.
Нечеткие алгоритмы
В настоящее время рынок так называемых нечетких контроллеров, которые используются в системах с элементами искусственного интеллекта и даже в стиральных машинах LG, оценивается миллиардами долларов [41]. Нечеткие алгоритмы реализуют сложные зависимости между нечеткими множествами, нечеткими высказываниями, а также и между так называемыми нечеткими числами. Нечеткий алгоритм – это последовательность нечетких инструкций. Инструкции классифицируются следующим образом [41]: 1) назначающие, например, «х – высокий», «у – маленький»; 2) нечеткие высказывания, например, «Если Х, то У иначе Z»; 3) безусловные активные, например, «немного увеличить х», «чуть левее z». Здесь могут добавляться и обычные «четкие» инструкции. Вначале может производиться фаззификация для получения нечетких множеств по точечным значениям. После получения результата может производиться дефаззификация – получение точечных значений выходных переменных. Разработаны специальные микропроцессоры, реализующие нечеткие алгоритмы. Управляющие устройства, основанные на нечеткой логике называют контроллерами нечеткой логики. В них вместо точных зависимостей используют формализованные с помощью лингвистических переменных знания экспертов. В настоящее время разработаны специальные пакеты программного обеспечения, реализующие нечеткие алгоритмы, например, FuzzyCalc.
ЛИТЕРАТУРА
1. Алешина Н.А., Анисов П.И. и др. Логика и компьютер. Моделирование рассуждений и проверка правильности программ. – М.: Наука, 1990. – 240 с. 2. Аляев Ю.А. Козлов О.А. Алгоритмизация и языки программирования Pascal, C++, Visual Basic: Учебно-справочное пособие. – М.: Финансы и статистика, 2002, 2004. – 320 с. 3. Аляев Ю.А.др. Практикум по алгоритмизации и программированию на языке Паскаль: Учеб. Пособие /Ю.А. Аляев, В.П. Гладков, О.А. Козлов. – М.: Финансы и статистика, 2004. – 528 с.
4. Белоусов А.И., Ткачев С.Б. Дискретная математика: Учеб. для вузов /Под ред. В.С. Зарубина, А.П. Крищенко. – М.: Изд.-во МГТУ им. И.Э. Баумана, 2001. – 744 с. 5. Бочаров В.А. Основы логики. – М.: Логос, 1994. –296 с. 6. Викентьев Л.Ф., Аляев Ю.А., Некрасов В.Г., Рачинский А.А. Основы дискретных автоматов. – Пермь: Тип. ПВВКИУ, 1985. – 196 с. 7. Вьюкова Н.И., Галатенко В.А., Ходулев А.Б. Систематический подход к программированию /Под ред. Ю.М. Баяковского. – М.: Наука, 1988. – 208 с. 8. Гетманова А.Д. Учебник по логике. – М.: ЧеРО, 2000. – 304 с. 9. Горбатов В.А. Основы дискретной математики /Учебное пособие для вузов. – М: Высшая школа, 1986. – 312 с. 10. Горбатов В.А. Фундаментальные основы дискретной математики. Информационная математика: Уч. пособ. для вузов. – М.: Наука, 2000. – 540 с. 11. ГОСТ 19.701-90. Схемы алгоритмов, программ, данных и систем. Условные обозначения и правила выполнения. – М.: Издательство стандартов, 1991. – 26 с. 12. Даль Владимир. Толковый словарь живого великорусского языка: В 4 т. Т. 1: А-З. – М.: ТЕРРА, 1994. – 800 с. 13. Дементьев В.А., Крылов Л.Н., Осипов В.П., Павлов Г.А., Прокошев Л.А. Теория и синтез дискретных автоматов /Под редакцией Дементьева В.А. –М.: МО СССР, 1979. – С. 7-33. 14. Дискретные устройства автоматизированных систем управления /Под ред. Г.Н. Тимонькина, В.С.Харченко. – М.: МО СССР, 1990. – 486 с. 15. Ивин А.А. Строгий мир логики. – М.: Педагогика, 1988. – 154 с. 16. Ивлев Ю.В. Логика: Учебник для вузов. – М.: Логос, 2001. – 272 с. 17. Коган Т.И. Дискретные устройства (автоматы). – Пермь: Тип. ПВВКИУ, 1985. – 208 с. 18. Коршунов Ю.М. Математические основы кибернетики. – М: Энергоатомиздат, 1987. – 496 с. 19. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. – М: Энергоатомиздат, 1988. – 450 с. 20. Лавров А.Н. Основы построения автоматизированных систем управления. Учебное пособие. – Пермь: ПВКИУ, 1980. – 320 с. 21. Мендельсон Э. Введение в математическую логику. – М.: Наука, 1976. – 320 с. 22. Могилев А.В., Пак Н.И., Хеннер Е.К. Информатика. – М.: Академия, 1999. – 816 с. 23. Непорожнев И.П. Элементы дискретной математики /Учебно-методическое пособие. – Пермь: ПВВКИКУ, 1994. – 38 с. 24. Нефедов В.Н., Осипова В.А. Курс дискретной математики. – М: Издательство МАИ, 1992. –264 с. 25. Никольская И.Л. Математическая логика. – М: Высшая школа, 1981. – 128 с. 26. Новиков Ф.А. Дискретная математика для программиста. – СПб.: Питер, 2001. – 502 с. 27. Ожегов С.И. Словарь русского языка: Ок. 57000 слов /Под ред. Н.Ю. Шведевой. – 16-е изд., испр. – М.: Рус. Яз., 1984. – 798 с. 28. Потемкин И.С. Функциональные узлы цифровой автоматики. – М.: Энергоатомиздат, 1988. – 258 с.
29. Робототехника и гибкие автоматизированные производства. В 9-ти кн. Кн.6. Техническая имитация интеллекта: Учеб. пособие для втузов /Под редакцией И.М. Макарова. – М: Высшая школа, 1986. – 144 с. 30. Савельев А.Я. Прикладная теория цифровых автоматов. – М.: Высш. школа, 1987. – 346 с. 31. Самофалов К.Г. Прикладная теория цифровых автоматов. – Киев: Высш. школа, 1987. – 456 с. 32. Тей А., Грибомон П. и др. Логический подход к искусственному интеллекту. – М.: Мир, 1990. – 432 с. 33. Тюрин С.Ф. Дискретные устройства (автоматы) систем автоматизированного управления и контроля. – Пермь: ПВВКИКУ, 1996. – 362 с. 34. Тюрин С.Ф. Проблема сохранения функциональной полноты булевых функций при «отказах» аргументов //Автоматика и телемеханика, 1999. № 9. – С. 176-186. 35. Тюрин С.Ф. Системы контроля технического состояния и диагностирования. – Пермь: ПВВКИКУ, 1995. – 148 с. 36. Энциклопедия. Том22. Информатика /Глав. ред. Е.А. Хабалина, вед. науч. ред. А.Г. Леонов. – М.: Аванта, 2003. – 624с. 37. Язык компьютера: Пер. с англ. /Под ред. И с предисл. В.М. Курочкина. – М.: Мир, 1989. – 264 с. 38. http://distance.ru/4stud/umk/logic/logic12.html 39.http://ulstu.ru/people/SOSNIN/umk/Basis_of_Artificial_Intelligence/m_lect.htm 40. http://www.auditorium.ru/books/339/philosophy/chap06.html#i06 41. http://www.plink.ru/tnm/g145.htm
ПРИЛОЖЕНИЕ 1 Варианты контрольных заданий по дисциплине «Дискретная математика»
Задание 1 [1]. Выполнить операции над множествами (для пункта 1); представить результат графически (для пункта 2) – заштриховать соответствующую область на диаграмме Эйлера для трех взаимно пересекающихся множеств A,B,C и записать в виде объединения пересечений с использованием, где необходимо, операции дополнения. Множества M,А,В,С – произвольные, множество I – универсальное (универсум), Æ – пустое множество. Вариант 1. 1) Æ\М=? 2) Вариант 2. 1) 2) Вариант 3. 1) 2) Вариант 4. 1) 2) Вариант 5. 1) Æ \I 2) Вариант 6. 1) 2) Вариант 7. 1) 2) Вариант 8. 1) 2) Вариант 9. 1) 2) Вариант 10. 1) Æ\M=? 2) Задание 2. По заданному десятичному числу, которое вычисляется следующим образом: 150 + номер по списку подгруппы, заштриховать на диаграмме Эйлера для трех взаимно пересекающихся множеств А,В,С соответствующую область и записать ее в виде объединения конституент единицы и пересечения конституент нуля. Задание 3. По заданному десятичному числу получить номер логической функции в двоичном, восьмеричном и шестнадцатеричном кодах. Составить таблицу истинности соответствующей логической (переключательной) функции. Определить СДНФ, СКНФ, символическую форму функции в десятичном и двоичном кодах. Минимизировать функцию по кубу соседних чисел. Определить свойства функции и представить вектор свойств в двоичном, восьмеричном и шестнадцатеричном кодах. Реализовать функцию переключательной схемой и функциональными схемами в базисах И-НЕ, ИЛИ-НЕ. Получить булевы производные по всем переменным. Представить функцию в базисе Жегалкина. Варианты заданий.
Задание 4.
Решить комбинаторную задачу. Вариант 1. 1. Сколькими способами можно набрать очки после 3-х выстрелов по мишени из 10 секторов? 2. Определить число вариантов перестановок разрядов в векторе 01032. 3. Имеется три типа снаряжения. Сколькими способами можно оснастить 5 спасателей? 4. Решить комбинаторное уравнение Вариант 2. 1. Сколькими способами можно занять места в аудитории, имеющей 15 мест, группой учащихся из 4-х человек? 2. Сколькими способами можно построить колонну из 3-х автомобилей 3-х типов? Перечислить варианты. 3. Сколькими способами можно выбрать подгруппу из 4-х учащихся из группы, состоящей из 8-ми человек? 4. Решить комбинаторное уравнение Вариант 3. 1. Сколько вариантов состояний имеет система из 9 подсистем, если каждая подсистема может находиться в 5-ти возможных состояниях? 2. Сколько комбинаций шифров можно получить перестановкой цифр в шифре 20287? 3. Сколькими способами можно выбрать пары состояний из пяти состояний системы? 4. Решить комбинаторное уравнение Вариант 4. 1. Сколько вариантов состояний имеет государство из 4-х губерний, каждая из которых может находиться в одном из следующих состояний: а) экономический рост, б) экономический спад, г) народные волнения? 2. Сколькими способами может руководитель фирмы назначить на 5 должностей 2-х специалистов с высшим образованием? Перечислить варианты. 3. Сколько разнополых пар могут составить трое юношей в обществе пяти девушек? 4. Решить комбинаторное уравнение Вариант 5. 1. Сколько комбинаций двоичных коэффициентов a,b,c,d имеется для уравнения ax-by+cz-dw=0? 2. Сколькими способами можно построить колонну из 3-х автомобилей? Перечислить варианты. 3. Сколькими способами можно составить наборы косметики из 4-х шампуней 3-х типов? 4. Упростить выражение Вариант 6. 1. Сколько трехцветных флагов можно предложить из материалов 4-х цветов? 2. Сколькими способами можно расставить автомобили 10 наименований по трем стоянкам, если на первую должно быть поставлено 3, на вторую – 5, а на третью – 2? 3. Сколькими способами можно выбрать три квартиры из предложенных восьми? 4. Решить комбинаторное уравнение Вариант 7. 1. Сколько существует вариантов приобретения тремя олигархами трех разнотипных корпораций? 2. Сколькими способами можно составить слова из символов &,*,^,$? 3. Сколькими способами можно выбрать два особняка в престижном районе Лондона из предлагаемых пяти? 4. Решить комбинаторное уравнение Вариант 8. 1. Сколькими способами пять семей приобретут по одной квартире в восьми квартирном доме? 2. Сколькими способами можно переставить 3 строки и 2 столбца некоторой матрицы? 3. Сколько можно выбрать подгрупп из 4-х специалистов, если в группе специалистов 7 человек? 4. Решить комбинаторное уравнение Вариант 9. 1. Подсчитайте число программ, не обязательно имеющих смысл, состоящих из 5 команд 3-х типов? 2. Сколькими способами можно переставить буквы в слове «перешеек»? 3. Сколько можно составить бригад из 5 инженеров 4-х специальностей? 4. Решить комбинаторное уравнение Вариант 10. 1. Подсчитайте число программ, не обязательно имеющих смысл, состоящих из 4-х команд 3-х типов? 2. Подсчитайте число последовательностей, получаемых перестановками символов в последовательности 0132? 3. Сколько пар можно выбрать из пяти студентов? 4. Упростить выражение Задание 5. Задан неориентированный граф без петель из пяти вершин строками полуматрицы смежности в виде шестнадцатеричного числа, где первая цифра – первая строка, вторая цифра – вторая строка и т.д. Изобразить по заданному шестнадцатеричному числу граф в виде рисунка и определить степени всех вершин, цикломатическое и хроматическое число. Получить матрицу всех путей в графе длиной 2 путем возведения в квадрат соответствующей булевой матрицы (вместо суммирования используется операция дизъюнкции). Варианты заданий.
Задание 6. Построить автомат – распознаватель последовательности. Варианты заданий.
Задание 7. Построить матрицу Хэмминга для заданного количества информационных разрядов 6. Варианты заданий.
ПРИЛОЖЕНИЕ 2 Варианты контрольных заданий по дисциплине «Математическая логика»
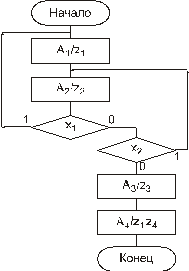
Задание 1. По заданной ГСА получить ЛСА, МСА, систему переключательных функций соответствующего автомата, схему автомата в базисе И-НЕ, ИЛИ-НЕ, ПЗУ, ПЗУ и мультиплексоре. Написать микропрограмму для автомата с двумя типами микропрограмм. Вариант 1.
Вариант 2.
Вариант 3.
Вариант 4.
Вариант 5.
Вариант 6.
Вариант 7.
Вариант 8.
Вариант 9.
Вариант 10.
Задание 2. Построить машину Тьюринга для распознавания последовательности символов на ленте. Построить машину Поста для той же задачи. Варианты заданий.
Задание 3. Формализовать высказывание. Получить СДНФ, СКНФ, ДНФ, КНФ. Представить высказывание в виде суперпозиции только следующих операций 1) «Штрих Шеффера», 2) «Стрелка Пирса», 3)»Импликация» и «Отрицание», 4) «Импликация» и «Константа нуля». Вариант 1. «Если я замолчу – возопиют камни и реки потекут вспять». Вариант 2. «Если возопиют камни или реки не потекут вспять, то я замолчу». Вариант 3. «Если мед есть, то горшок становится пустым, а Винни-Пух – сытым». Вариант 4. «Студент сдает зачет на 4 или на 5 тогда и только тогда, когда добросовестно решает задачи по математической логике». Вариант 5. «Если я сдам зачет по математической логике, то пойду в казино или в кино». Вариант 6. «А тогда и только тогда, когда В тогда и только тогда, когда С». Вариант 7. «Если зажигают звезды, то это кому-нибудь нужно; все это – тогда и только тогда, когда не хлебом единым жив человек». Вариант 8. «Неверно, что если число делится на 3 и 2, то оно делится на 10». Вариант 9. «Если студент сдает зачет по математической логике, то неверно, что его отчисляют от обучения и выдают документы». Вариант 10. «Студент не сдает зачет тогда и только тогда, когда он не выполнил контрольную работу и не имеет конспекта лекций». Задание 4. Доказать или опровергнуть общезначимость формулы, используя законы алгебры логики и формулы равносильных преобразований, а также путем построения дерева доказательства. Вариант 1.
Вариант 2.
Вариант 3.
Вариант 4.
Вариант 5.
Вариант 6.
Вариант 7.
Вариант 8.
Вариант 9.
Вариант 10.
Задание 5. Проверить аргумент методом резолюций. Получить все следствия из данных посылок. Вариант 1. «Если объект не обладает свойством X или обладает свойством Y, то он обладает свойством Z. Если объект обладает свойством X, то он обладает свойством Y. Следовательно, объект обладает свойством Z». Вариант 2. «Если Петр поедет в Сан-Франциско, то Иван поедет на Канары. Петр поедет в Чикаго или в Сан-Франциско. Если Петр поедет в Чикаго, то Анна останется в Москве. Но Анна не останется в Москве. Следовательно, Иван поедет в Канны». Вариант 3. «Если неверно, что X или Y, то и Z, и W. Не Z или не W. Следовательно, X или Y». Вариант 4. «Если сегодня вечером будет дождь, то я пойду в казино. Если завтра будет снег, то я пойду на дискотеку. Сегодня вечером будет дождь или завтра будет снег. Следовательно, я пойду в казино или на дискотеку». Вариант 5. «Если функция линейная или монотонная, то если она самодвойственна, то сохраняет константу нуля. Данная функция и нелинейна, и немонотонна. Следовательно, она самодвойственна и сохраняет константу нуля». Вариант 6. «Галя и Борис – ровесники или Галя старше Бориса. Если Галя и Борис – ровесники, то Оля и Борис разного возраста, Если Галя старше Бориса, то Борис старше Коли. Следовательно, Оля и Борис – разного возраста или Борис старше Коли». Вариант 7. «Если X, то (Y тогда и только тогда, когда Z). Если X, то Z и (если Z, то Y). Следовательно, X». Вариант 8. «Если студент допущен к экзамену, то он сдал контрольную работу. Студент сдает контрольную работу, если научится проверять правильность аргументов методом резолюций. Студент не разобрался в этом методе. Следовательно, студент не допущен к экзамену». Вариант 9. «Если и X, и Y, то и Z, и не Y. Не Z или Y. Следовательно, не Y или не X». Вариант 10. «Если я достану учебник или конспект, то сдам экзамен. Если мой приятель не уедет в Кембридж, то я достану учебник. Если я достану конспект, то он уедет в Кембридж. Значит, я сдам экзамен». Задание 6. Формализовать умозаключение по заданному модусу в логике предикатов. Доказать или опровергнуть умозаключение по заданному модусу методом резолюций с использованием двух моделей. Модель 1.
Модель 2.
Варианты заданий.
[1] Задания подготовлены А.М. Гревцевым
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 896; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.79.237 (0.016 с.) |


 .
.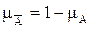 .
.
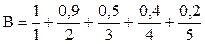 ;
; .
.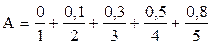
 ;
; .
.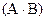 U
U 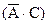 . При этом Х – область рассуждения для высказывания А, Y – область рассуждения для высказывания В, и в общем случае они разные. Если С не указано и универсум Y области рассуждения для высказывания В, то получаем
. При этом Х – область рассуждения для высказывания А, Y – область рассуждения для высказывания В, и в общем случае они разные. Если С не указано и универсум Y области рассуждения для высказывания В, то получаем  [41]. При этом функция принадлежности пары определяется как минимум функций принадлежности элементов пары.
[41]. При этом функция принадлежности пары определяется как минимум функций принадлежности элементов пары. ;
;  .
. Или в виде табл. 97:
Или в виде табл. 97: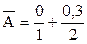 .
. Или в виде табл. 98:
Или в виде табл. 98:


 .
. ; Con(А)=
; Con(А)= 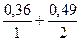 ;
; ; Dil(В)=
; Dil(В)=  .
.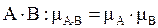 ;
; .
.
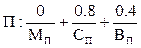 .
.
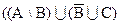 =?
=? ?
?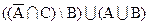 =?
=? ?
? =?
=? ?
? =?
=?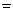 ?
? =?
=? ?
? =?
=? ?
? =?
=? ?
? =?
=? ?
?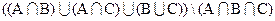 =?
=? =?
=? .
. .
. .
. .
.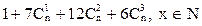 .
. .
. .
. .
.








 .
.


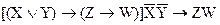 .
.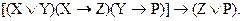


 .
.