
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кванторы и связанные переменныеСодержание книги
Поиск на нашем сайте
Все формулы логики высказывания являются частными случаями логики предикатов. Все операции логики высказывания переносятся в логику предикатов для связывания предметных букв. Дополнительно используются обозначения кванторов: "x F(х), т.е. «Все х обладают свойством F»; "$x F(х), т.е. «Некоторые х обладают свойством F (но возможно и все)», где "– квантор общности, $– квантор существования. Квантор общности и квантор существования называются двойственными. Иногда используют обозначения квантора «Равно один»: $!. Если переменная связана квантором, то она называется связанной, иначе – свободной. Например: "x F(x,y), $x F(x,y), здесь x – связанная переменная, y – свободная переменная.
Синтаксис языка логики предикатов. Формулы логики предикатов и формализация суждений
В качестве алфавита в логике предикатов используется латинский язык, как и в логике высказываний [25]. Вводятся следующие обозначения: · константы: a,b,c,d,e,... – строчные буквы из начала латинского алфавита; · логические константы (0 – ложь, 1 – истина); · предметные переменные: x, y, z, v, w,... – строчные буквы из конца латинского алфавита; · функции: f,g,h,... –строчные буквы из середины латинского алфавита; · предикатные символы: F, G, H, P, Q,... – прописные буквы латинского алфавита; · символы логических операций и кванторов (¯, |, Ú, ®,Ù, · служебные символы, например, символы скобок ([, ], {, }, (,)). Символы функций и предикатов называют сигнатурой. Функции и предикаты иногда снабжаются верхним индексом местности операции. При определении формулы используется понятие «терм». Терм – объединяет понятия переменных и функций, к которым применяются предикатные буквы. Всякая предметная переменная или константа – терм. Если f – n-местная функция, а t1,t2,...,tn – терм, то fn(t1,t2,...,tn) – тоже терм. Никакие другие выражения не являются термами. Пример. f3(a,x,g2(x,y)) – это терм с трехместной функцией f, двухместной функцией g, a – константа. Если F – n-местный предикат, t1,t2,...,tn – термы, то Fn(t1,t2,...,tn) – элементарная формула. Никакие другие выражения не являются элементарными формулами. Элементарную формулу иногда называют атомарной или атомом. Введем понятие формула: 1) всякая элементарная формула – это формула; 2) если F и Q – формулы, а х – предметная переменная, которая входит в F, то "x F(x), $x F(x), Примеры. P2(a,f1(x)) – формула; Q1(x,g2(x,b)) – не формула, так как предикат Q должен быть одноместным; P2(y,Q1(z)) – не формула, так как Q1(z) – не терм; f1(g2(x,y)) – не формула, а терм; F2(a,y)®Q1(b) – формула.
|
||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 454; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |


 ,…);
,…);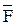 , F× Q, FÚ Q, F® Q, F«Q – являются формулами.
, F× Q, FÚ Q, F® Q, F«Q – являются формулами.


