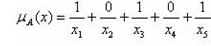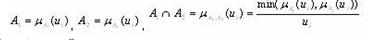Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нечеткие множества в решении экономических задачСодержание книги
Поиск на нашем сайте
В процессе создания моделей баз знаний специалисты сталкиваются с проблемой отражения и использования нечеткой, то есть неопределенной информации. Представление таких знаний как «высокий человек», «добросовестный поставщик», «надежный партнер» и т.д., потребовали нового взгляда на методы их формализации. Задачи, решаемые человеком, в большинстве случаев опираются именно на нечеткие, размытые и неопределенные знания о процессах или событиях. Знания человека в большинстве случаев нечеткие. Он оперирует такими понятиями как высокий, низкий, горячее, холодное, бедный, богатый и т.д. в повседневной производственной практике и быту. Нечёткое (или размытое, расплывчатое, туманное, пушистое) множество – понятие, введённое Лотфи Заде в 1965 г. Он расширил классическое понятие множества, допустив, что характеристическая функция (функция принадлежности элемента множеству) может принимать любые значения в интервале [0,1], а не только значения 0 или 1. Для того чтобы такого рода знания можно было использовать для формирования решений, в 1965 году Л.Заде предложил теорию нечетких множеств. В основе данной теории лежит понятие функции принадлежности, которая указывает степень принадлежности какого-либо элемента некоторому множеству элементов. Данная функция является субъективной и строится на основании знаний, опыта или ощущений некоторого субъекта к какому-либо объекту, процессу, явлению и т.д. Степень принадлежности элементов множества Е множеству А можно однозначно представить как:
На рисунке иллюстрируется четкая (однозначная) принадлежность элементов одного множества другому
Но принадлежность элементов может характеризоваться и приблизительно, например:
Функция принадлежности нечёткого множества – обобщение индикаторной функции классического множества. В нечёткой логике она представляет степень принадлежности каждого члена к данному нечёткому множеству. Степени принадлежности часто смешивают с вероятностями, хотя они принципиально отличны Для нашего случая функция принадлежности, записывается следующим образом:
Если функцию принадлежности применить для четких множеств (см. рис. 5.33), то можно получить следующее:
Как правило, функции принадлежности иллюстрируются графически. На рисунке представлено субъективное понимание возраста с помощью функций принадлежности и графиков.
На рис. 5.35 представлено субъективное понимание понятия «низкие процентные ставки».
Для того чтобы функцию принадлежности можно было использовать в практических расчетах, вводятся операции пересечения и объединения нечетких множеств. Операция пересечения нечетких множеств соответствует нахождению минимум а значений их функций принадлежности:
Операция объединения соответствует максимуму значений их функций принадлежности, то есть:
Пример применения нечетких множеств В ходе управления финансами очень часто возникает задача борьбы с неопределенностью, сопровождающей финансовые решения. Неопределенность эта двоякая: а) текущее состояние финансовой системы не может быть распознано с необходимой точностью; б) будущие показатели финансовой системы и ее внешнего окружения неизвестны вполне точно. Нечеткие множества в этом смысле могут выступать как инструмент моделирования неопределенности, который базируется на известной мыслительной способности человека оперировать качественными категории и оформлять свои логические выводы также в качественной форме. Если качество некоторого объекта может быть выражено некоторой иерархией количественных и/или качественных признаков, причем известно, как одни факторы доминируют над другими в пределах одного уровня иерархии, то оказывается возможным оценить комплексное качество объекта на основе того же для отдельных свойств иерархии. Оценка качества – это квалиметрия. Характерные задачи квалиметрии в финансовом менеджменте: оценка риска банкротства предприятия, оценка надежности акций и облигаций, выбор управляющей компании, оценка перспективности приобретения недвижимости, стоимостная оценка банковских залогов и т. д. Если речь идет об операциях с будущими значениями финансовых факторов, то удобно моделировать эти факторы как нечеткие числа и функции. Тогда можно получить итоговые результаты моделирования в таком же виде – и оценить риск того, что эти финансовые результаты окажутся ниже предустановленных нормативов.
Характерные приложения теории нечётких множеств к финансовому менеджменту следующие:
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 385; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.244.34 (0.006 с.) |

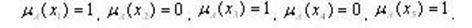

 более или менее принадлежит;
более или менее принадлежит;