Семантическая сеть – это ориентированный граф, вершины (узлы) которого соответствуют понятиям моделируемой предметной области, а дуги – отношениям между ними.

В качестве понятий обычно выступают конкретные или абстрактные объекты, а отношений – связи.

Семантические сети содержат описание связей в явной форме, указанных с помощью синтаксических, семантических и прагматических отношений.

Наиболее часто в них используется следующие отношения:

целое-часть (класс – подкласс, элемент – множество и т.д.);

функциональная связь, определяемая глаголом (производит, находится, поставляет … и т.д.);

атрибутивные (иметь значение, иметь свойство);

логические (И, ИЛИ, НЕТ);

временные (в течение, раньше, позже…).

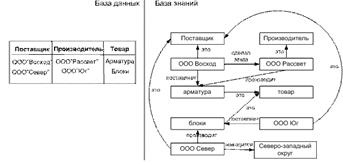
Пояснить базу знаний легче в сравнении с базой данных, так как различия между ними нечеткие (размытые).

На рисунке ниже представлена информация о поставках, поставщиках и прочее с помощью реляционной базы данных и базы знаний в виде семантической сети.

Сравнивая базу данных и базу знаний видим, что в базе данных информация более скудная и поэтому с уверенностью трудно ответить на вопрос:

Делал ли ООО «Восход» заказ ООО «Рассвет» на арматуру, которую тот производит или ООО»Восход» поставил арматуру, которую произвел ООО «Рассвет»?

Отличие баз знаний от баз данных состоит в том, что первые содержат связи между объектами в явной форме.

Обрабатывается семантическая сеть на основе принципа сопоставления объекта и отношений, указанных в запросе, с объектами и отношениями, имеющимися в семантической сети.

Дерево вывода в решении экономических задач

Кратко рассказать Вопрос 4.22

Дерево вывода – это множество объединенных правил, отражающих условия выполнения некоторого процесса.

Правила представляют собой языковую конструкцию вида:

ЕСЛИ <условие, ct(условия)>, ТО <заключение, ct(заключения)> ct(правила),

где ct(условия) – коэффициент определенности условия;

ct(заключения) – коэффициент определенности заключения;

ct(правила) – коэффициент определенности правила.

Коэффициент ct, равный 0, указывает на полную неопределенность, равный 1 – на полную определенность.

Правила и коэффициенты задает эксперт.

Множество правил объединяются в дерево вывода.

Например задано два правила.

Правило 1.

ЕСЛИ

индекс цен возрастет не менее чем на 3% (условие В) ct(В)

И

цены на энергоносители вырастут не более чем на 19% (условие С), ct(С) = 0,4

ТО акции покупать (заключение А) ct(А) =0,7, ct(правила 1) = 0,7.

Правило 2.

ЕСЛИ ВВП возрастет не менее чем на 1,5% (условие Д) ct(Д) = 0,8

ИЛИ

ставки Центрального банка будут в пределах 12% (условие Е) ct(Е) = 0,5

ИЛИ

объем экспорта возрастет более чем на 5% (условие G) ct(G) = 0,6

ТО индекс цен возрастет не менее чем на 3%. (заключение В) ct(В) = 0,3, ct(правила 2) = 0,3.

Эти правила объединяются в дерево, представленное на рисунке ниже.

Знания такого рода представляются графически, а также как рассчитывается коэффициент определенности заключения.

Условимся заключение, получаемое с помощью правила, изображать сверху, а условия – снизу.

Число рядом с условием указывает на его определенность, а число рядом с линией – на определенность самого правила.

Условий в правиле может быть несколько, которые связанны между собой союзами И или ИЛИ.

Например

ЕСЛИ А и В и С, ТО Е,

ЕСЛИ А или В или С, ТО Е.

Графически эти правила изображаются так, как это показано на рисунке

Сплошная или пунктирная дуга указывает на вид объединения условий: союзом И или союзом ИЛИ соответственно.

Число, находящееся рядом с дугой (сплошной или пунктирной), указывает на определенность правила, а число рядом с условиями и заключениями – на определенность условий и заключений.

Лицо, принимающее решение, условиям (А, В, С), а также правилу присваивает коэффициент определенности от 0 до 1.

С помощью специальных формул рассчитывается коэффициент определенности для заключения.

Для простого правила, содержащего лишь одно условие, например, ЕСЛИ Е, ТО С, коэффициент определенности для заключения С рассчитывается так:

ct(C) = ct(E) – ct(правила)

где ct(C) – коэффициент определенности заключения С;

ct(E) – коэффициент определенности условия Е;

сt(правила) – коэффициент определенности правила.