Общие принципы построения интеллектуальных систем управления на основе нечеткой логики.

Применение нечеткой логики обеспечивает принципиально новый подход к проектированию систем управления, “дорыв'' в новые информационные технологии, гарантирует возможность решения широкого круга проблем, в которых данные, цели и ограничения даются слишком сложными или плохо определенными и в силу этого не поддаются точному математическому описанию.

Возможны различные ситуации, в которых могут использоваться нечеткие модели динамических систем:

- когда имеется некоторое лингвистическое описание, которое отражает качественное понимание (представление) процесса и позволяет непосредственно построить множество нечетких логических правил;

- имеются известные уравнения, которые (хотя бы грубо) описывают поведение управляемого процесса, но параметры этих уравнений не могут быть точно идентифицированы;

- известные уравнения, описывающие процесс, являются слишком сложными, но они могут быть интерпретированы нечетким образом для построения лингвистической модели;

- с помощью входных/выходных данных оцениваются нечеткие логические правила поведения системы.

Первые результаты практического применения алгоритмов нечеткой к у правлению реальными техническими объектами были опубликованы в 1974 г. в работах профессора Лондонского Королевского колледжа Э.Х.Мамдани, посвященных проблеме регулирования парогенератора для электростанции. В этих работах была предложена сегодня классической структурная схема системы нечеткого управления в соответствии с рисунком 3.1.

Под нечетким управлением (Fuzzy Control) в данном случае понимается стратегия управления, основанная на эмпирически приобретённых знаниях относительно функционирования объекта (процесса), представленных в лингвистической форме в виде некоторой совокупности правил.

Рисунок 3.1 - Структурная схема системы нечеткого управления

На рисунке 3.1 ДФ - динамический фильтр, выделяющий, помимо сигналов ошибок управления x1=r1-y1 и x3=r2-y2,производные от этих сигналов x2=x1 и x4=x3;

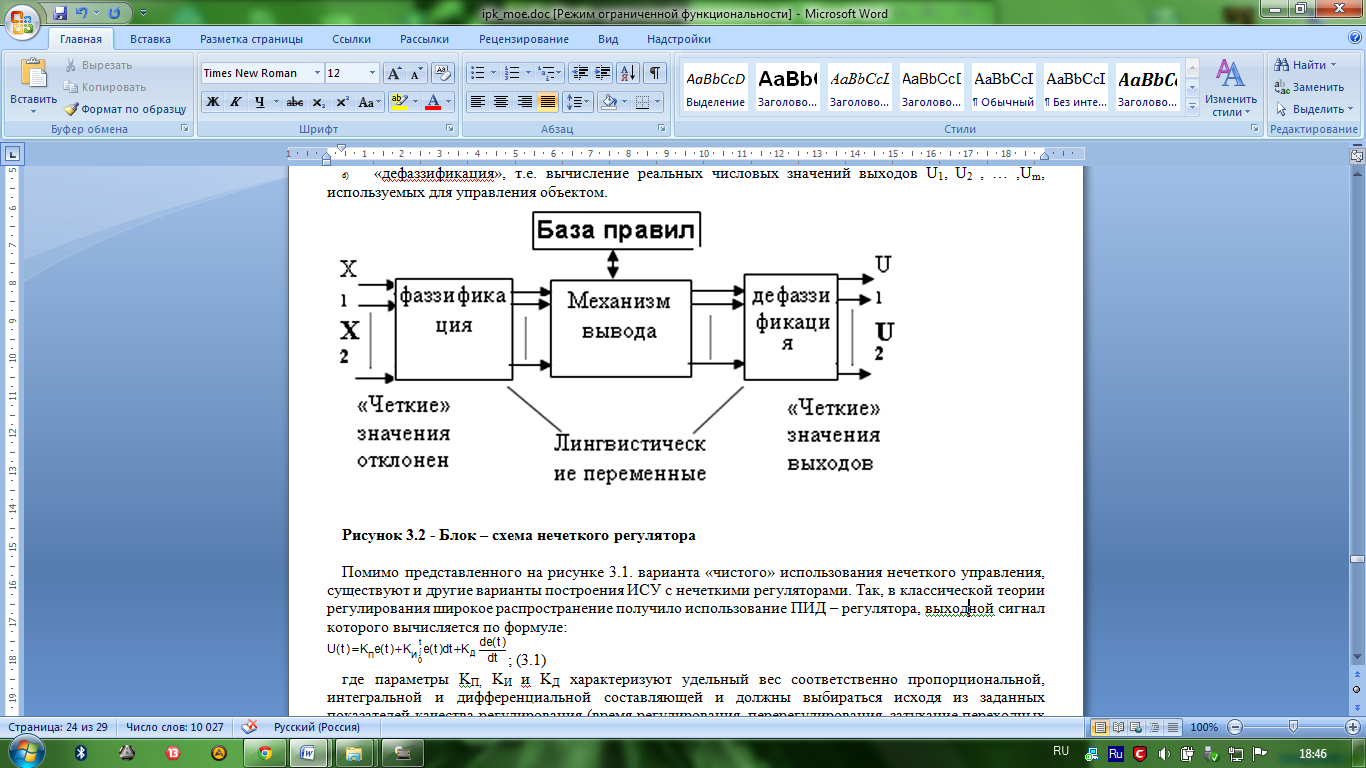
РНЛ- регулятор на основе нечеткой логики (“нечеткий регулятор”)включающий в себя базу знаний (конкретнее – базу правил) и механизм логического вывода;

r=(r1,r2)^Т,x=(x1,x2,x3,x4)^Т, u=(u1,u2)^Т и y=(y1,y2)^Т - соответственно векторы задающих воздействий (уставок),входов и выходов РНЛ, а также выходов объекта управления;

т-операция транспонирования вектора.

В качестве входов и выходов РНЛ выступают:

x1=Pe-отклонение давления в паровом котле (y1) по отношению к его требуемому значению (r1);

x2=Cpe-скорость изменения Pe;

x3=Se-отклонение скорости изменения давления (y2) по отношению к его заданному значению (r2);

x4=Cse - скорость изменения Se;

u1=Hc-изменение степени подогрева пара;

u2=Tc- изменение положения дросселя.

Мамдани предложил рассматривать эти величины как лингвистические переменные, каждая из которых может принимать одно из следующих значений из множества

L={NB, NM, NS, NO, PO, PS, PM, PB}.

Здесь 1-я буква в обозначении указывает знак числовой переменной и соответствует английскому слову Negative (“отрицательное”) или Positive (“положительное”), 2-я буква говорит об абсолютном значении переменной: Big, Middle, Small или O (“близкое к нулю”).На пример, символ Ns означает ”отрицательное малое”.

Блок – схема нечеткого регулятора в общем случае принимает вид, изображенный на рисунок 3.2.

Как видно из данной схемы, формирование управляющих воздействий U₁, U₂ , …,U_m включает в себя следующие этапы:

a) Получение отклонений управляемых координат и скоростей их изменения - X₁, X₂ , …,X_n;

b) «Фаззификация» этих данных, т.е. преобразование полученных значений к нечеткому виду, в форме лингвистических переменных;

c) определение нечетких (качественных) значений выходных переменных U₁, U₂ , …,U_m (в виде функций их принадлежности их соответствующим нечетким подмножествам) на основе заранее сформулированных правил логического вывода, записанных в базе правил;

d) «дефаззификация», т.е. вычисление реальных числовых значений выходов U₁, U₂ , …,U_m, используемых для управления объектом.

Рисунок 3.2 - Блок – схема нечеткого регулятора

Помимо представленного на рисунке 3.1. варианта «чистого» использования нечеткого управления, существуют и другие варианты построения ИСУ с нечеткими регуляторами. Так, в классической теории регулирования широкое распространение получило использование ПИД – регулятора, выходной сигнал которого вычисляется по формуле:

; (3.1)

где параметры K_П, K_И и K_Д характеризуют удельный вес соответственно пропорциональной, интегральной и дифференциальной составляющей и должны выбираться исходя из заданных показателей качества регулирования (время регулирования, перерегулирования, затухание переходных процессов). Возможное использование нечеткого регулятора для автоматической настройки (адаптации) указанных параметров ПИД – регулятора показано на рисунке3.3.

Рисунок 3.3 - Структура ИСУ с нечетким регулятором