
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точность представления чиселСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
БЦВМ оперирует с приближенными числами. Приближенным числом называется число х, мало отличающееся от точного значения числа X. Если х<Х, то х называется приближенным числом X по недостатку. Если х>Х, то х называется приближенным числом X по избытку. Погрешностью Ах приближенного числа х называется разность
Чаще всего знак ошибки неизвестен, поэтому целесообразно пользоваться абсолютной погрешностью приближенного числа
Чтобы судить о степени точности представления чисел в машине или степени точности вычисления, часто недостаточно знать абсолютную погрешность. Поэтому целесообразнее характеризовать точность представления или вычисления не абсолютной, а относительной погрешностью
т. е. составляет половину единицы младшего разряда. Минимальная и максимальная относительные погрешности соответственно будут:
Диапазон изменения погрешности можно определить из соотношения
Отсюда следует, что величина относительной погрешности сильно зависит от величины самого числа. Наименьшая относительная погрешность представления достигается в том случае, если число близко к единице по абсолютному значению. В машинах с плавающей точкой абсолютная погрешность при оптимальном округлении
Минимальная и максимальная относительные погрешности с ответственно равны:
Диапазон изменения погрешности
Следовательно, относительная погрешность изменяется в значительных пределах, а точность представления больших и малых чисел изменяется незначительно. В машинах с фиксированной точкой малый диапазон изменения чисел приводит к необходимости масштабировать задачи, а с уменьшением величины числа увеличивается погрешность представления. В машинах с плавающей точкой большой диапазон изменения чисел не требует масштабировать задачи. В них обеспечивается высокая точность представления больших и малых мантисс чисел. Вследствие этого в ходе вычислительно процесса ошибка вычислений не накапливается так быстро, в машинах с фиксированной точкой. Погрешность результата в основном зависит от методических ошибок, появляющихся вследствие использования приближенных формульных зависимостей; от ошибок входных данных (первичных ошибок, измерителей, ошибок представления) и ошибок, вносимых самой БЦВМ в процессе обработки информации в конечной разрядной сетке. Конечная разрядная сетка — основная причина возникновения ошибок округления, которые имеют тенденцию к накоплению при увеличении количества операций, выполняемых с округлением. В дальнейшем ошибки округления, трансформированные через алгоритм, отдельные последовательности операций, будем называть вычислительными погрешностями. Величина вычислительной погрешности на выходе реализуемого алгоритма зависит от числа операций, выполняемых с округлением, геометрии связей операндов, длины разрядной сетки, формы представления чисел и способа округления результатов операций. Суммарная погрешность вычислений зависит от всех перечисленных факторов, и стремление повысить точность результата, воздействуя лишь на один из них, может не дать положительного эффекта.
Методическая погрешность. Основой любого бортового алгоритма является математическое описание физического объекта или процесса. Этапу программирования предшествует представление математического описания задачи в терминах численного анализа. Такое представление оказывается всегда приближенным, вследствие чего возникает методическая погрешность. Источником методических погрешностей являются погрешности численных методов, поэтому эти погрешности могут быть доведены до желаемых значений исходя из общей теории приближенных вычислений. Трансформированная погрешность. При обработке числовой информации на результирующую погрешность существенное влияние оказывают ошибки исходных данных, которые возникают из-за неточности измерений и невозможности представления некоторых числовых величин конечным числом значащих цифр (иррациональные числа, некоторые дроби, конечные в одной системе счисления и бесконечные в другой). В качестве исходной информации может также служить приближенное решение, полученное на предшествующем шаге вычислений. Таким образом, при реализации алгоритма, исходная информация для которого представлена приближенно, будет получен результат, содержащий некоторую погрешность, называемую трансформированной. Инструментальная погрешность. Методическая и трансформированная погрешности определяют точность решения независимо от способа вычисления. Если рассмотреть реализацию алгоритма в БЦВМ, то в приближений результат вносится погрешность, вызванная ограниченной точностью выполнения некоторых арифметических операций. Погрешности этих арифметических операций зависят от ограниченной разрядной сетки, формы представления чисел и способа округления результатов операций. Инструментальная погрешность зависит, главным образом, от способа вычислений, т. е. типа вычислительной машины, где происходит переработка количественной информации. Суммарная погрешность алгоритма. Программа решения задачи на бортовых ЦВМ состоит из операторов, выполняющих следующие основные функции: пересылку чисел; преобразование чисел; управления процессом вычислений.
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 477; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.78.182 (0.008 с.) |



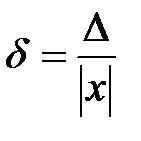 В машинах с фиксированной точкой величина абсолютной погрешности
В машинах с фиксированной точкой величина абсолютной погрешности  зависит от количества разрядов в мантиссе и способа округления. При оптимальном округлении абсолютная погрешность
зависит от количества разрядов в мантиссе и способа округления. При оптимальном округлении абсолютная погрешность








