
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Стационарные оптимальные линейные фильтрыСодержание книги
Поиск на нашем сайте
Предполагается, что на вход фильтра действует сумма сигнала
Сигнал и помеха представляют собой стационарные нормальные случайные процессы с нулевыми средними значениями, известными корреляционными ф-циями Линейный стационарный фильтр полностью характеризуется импульсной, переходной ф-цией
В общем случае колебание на выходе фильтра
Фильтр должен минимизировать величину
При статистической независимости
Комплексная передаточная ф-ция оптимального фильтра (без учета требований физической реализуемости, когда условие
а средний квадрат значения ошибки воспроизведения равен:
Из ф-л (7-305) и (7-306) видно, что при указанных условиях, когда сигнал и шум представляют собой независимые стационарные нормальные случайные процессы с нулевыми средними значениями, различие сигнала и шума заключено только в спектральных плотностях. При этом задача фильтрации состоит в том, чтобы по возможности полнее воспроизвести спектр сигнала и в максимальной степени подавить спектр помехи. Чем меньше перекрываются спектры сигнала и помехи, тем меньше ошибка воспроизведения. Если спектры не перекрываются совсем, то из (7-306) видно, что ошибка воспроизведения становится равной нулю. Фильтр, характеризуемый ф-лой (7-305), физически не реализуем. При вычислении комплексной передаточной ф-ции этого фильтра
интегрирование ведется в пределах от
Оптимальная нелинейная фильтрация Предполагается, что на входе приемника имеется сумма помехи и сигнала. Помеха представляет собой нормальный белый шум с нулевым средним значением. Сигнал
Рис. 7-79. Схема оптимального нелинейного фильтра. Устройства подобного типа находят широкое практическое применение. На вход фильтра подается напряжение
Имеющийся в схеме линейный фильтр предназначается для наилучшего отфильтровывания белого шума и минимизации среднего квадрата разности:
Так как постоянная составляющая полезного сообщения, являющаяся априорно известной, на выход фильтра не проходит, то ее восстанавливают с помощью схемы суммирования. Фильтры. В радиоэлектронных устройствах широкое применение находит такой вид линейных цепей (чаще их называют четырехполюсниками), как электрические фильтры, предназначенные для выделения (пропускания) или подавления (ослабления) сигналов с заданным спектром частот. Область частот, в которой фильтры обладают малым ослаблением (затуханием), называется полосой пропускания. Область частот, в которой фильтрысущественно ослабляют сигнал, определяется как полоса задерживания (заграждения, подавления).
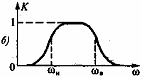
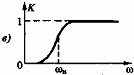
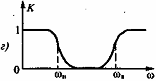
По характеру расположения полосы пропускания и полосы задерживания фильтры разделяются на четыре основных вида: 1. Фильтры нижних частот (ФНЧ), полоса пропускания которых расположена в области частот от 2. Фильтры верхних частот (ФВЧ), полоса пропускания которых простирается от некоторой граничной нижней частоты 3. Полосовые фильтры (ПФ), имеющие полосу пропускания в области между граничной нижней частотой 4. Режекторные, или заграждающие фильтры (РФ), полоса задерживания которых расположена в области частот от
Рис. 3.48. Амплитудно-частотные характеристики фильтров: а — нижних частот, б —верхних частот; в — полосового; г —режекторного 54. Вероятность и информация. Информационное содержание сигнала. Понятия «информация» (от лат. informatio — разъяснение, изложение) и «сообщение» в настоящее время неразрывно связаны между собой. Эти понятия сложны, близки по смыслу, и дать их точные определения через более простые достаточно трудно. Под информацией подразумевается совокупность сведений о каких-либо событиях, явлениях или предметах, предназначенных для передачи, приема, обработки, преобразования, хранения или непосредственного использования. Особенность информации состоит в том, что обычно возникает она в одном месте, а используется в другом. Передача информации — это процесс переноса сведений из одной точки пространства в другую. Отметим, что информацию, представленную в алфавитно-цифровой форме, в теории электросвязи принято называть данными. При вероятностном подходе информации рассматривается как сообщение о исходе случайных событий реализует случайную величину и функцию, а количество информации ставиться в зависимость от априорных вероятностей этих событий, величин, функций, если получаемое сообщение часто встреча(ное) событиях, Вероятность появления которых стремиться к 1, т.е. к достоверным сообщениям, то такое сообщение мало информативно. Большинство видов информации можно свести к двоичным явлениям (да, нет). Это пара явлений будет простейшим элементам информации. События – это элементарное явление, которое может быть с вероятностью от 0 до 1, т.е. вероятность = 0 до – вероятность = 1, или не быть вероятностью стремящейся к Q=1-P (P-вероятность) Когда P = 0.5 будет наибольшая неопределённость в ситуации События – это наибольше возможные некоторого опыта, где все исходы составляют «ансамбль» событий. (т.е. полная группа событий). Для ансамбля сумма вероятности событий равна.
В общем случае вероятности не остаются существующими, они могут изменяться во времени. Это характерно для астацинарного процесса, при стационарном процессе остальные характеристики не изменяются. Информационное содержание сигнала. Информация, подлежащая передаче и выраженная в определенной форме, называется сообщением. Сообщение может быть представлено в форме текста телеграммы, некоторых сведений, передаваемых по телефону, радио или телеграфу, телевизионного изображения, данных на выходе компьютера и т.д.
Ценность любых сведений, содержащихся в переданном получателю сообщении, характеризует количество заключенной в нем информации. Данная величина может определяться степенью изменения поведения получателя под воздействием принятого сообщения. В теории связи количественная оценка информации основывается на концепции выбора наиболее важного сообщения из всей совокупности возможных сообщений. При этом чем менее вероятен выбор данного сообщения, т.е., чем более оно неожиданно для получателя, тем большее количество информации в нем содержится. Совершенно очевидно обратное: достоверное (заранее известное) сообщение нет смысла передавать, поскольку оно не является неожиданным и, следовательно, не содержит никакой информации. Поэтому любые реальные сообщения следует рассматривать как случайные события (случайные процессы). В общем случае передаваемое по каналам связи сообщение можно представить в виде набора некоторых смысловых элементов или символов (например, букв какого-либо алфавита). Если общее количество (объем) смысловых символов равно т, а одно сообщение составлено из п элементов, то число возможных сообщений N = Сигнал (от лат. signum — знак) — физический процесс (или явление), несущий информацию о состоянии какого-либо объекта наблюдения. По своей физической природе сигналы могут быть электрическими, световыми, звуковыми и др. В радиотехнике в основном используются электрические сигналы.
|
|||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 521; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.201.92 (0.009 с.) |

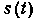 и шума
и шума 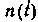 :
: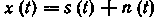
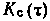 и
и 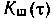 и соответствующими энергетическими спектрами
и соответствующими энергетическими спектрами 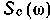 и
и 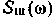
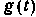 , связанной с частотно-передаточной ф-цией
, связанной с частотно-передаточной ф-цией 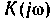 преобразованием Фурье:
преобразованием Фурье: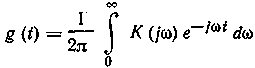
 определяется через входное колебание
определяется через входное колебание 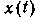 соотношением
соотношением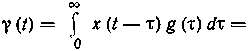
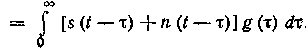
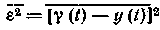
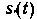 и
и 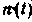 импульсная переходная характеристика оптимального фильтра
импульсная переходная характеристика оптимального фильтра 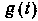 является решением интегрального уравнения Винера—Хопфа [7, 19]
является решением интегрального уравнения Винера—Хопфа [7, 19]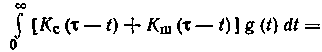
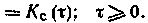 (7-304)
(7-304)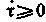 не принимается во внимание) определяется соотношением
не принимается во внимание) определяется соотношением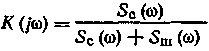 , (7-305)
, (7-305)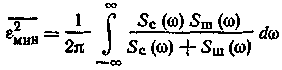 (7-306)
(7-306)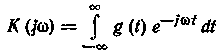 (7-307)
(7-307)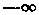 до
до 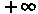 , и, следовательно, предполагается существование отличного от нуля отклика до момента появления сигнала
, и, следовательно, предполагается существование отличного от нуля отклика до момента появления сигнала 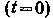 Тем не менее полученный результат представляет несомненный интерес, т. к. определяет потенциальную точность воспроизведения процесса: ни один реальный фильтр не может дать меньшей ошибки. Одним из направлений развития теории оптимальной линейной фильтрации является т. н. «калмановская фильтрация», в рамках которой характеристики сигналов непосредственно не задаются, а рассматривается дифференциальное уравнение системы, порождающей эти сигналы.
Тем не менее полученный результат представляет несомненный интерес, т. к. определяет потенциальную точность воспроизведения процесса: ни один реальный фильтр не может дать меньшей ошибки. Одним из направлений развития теории оптимальной линейной фильтрации является т. н. «калмановская фильтрация», в рамках которой характеристики сигналов непосредственно не задаются, а рассматривается дифференциальное уравнение системы, порождающей эти сигналы.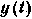 является высокочастотным колебанием, изменения одного из его параметров представляют собой полезное сообщение;
является высокочастотным колебанием, изменения одного из его параметров представляют собой полезное сообщение; 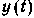 является медленным нормальным случайным процессом, т. е. время корреляции сообщения много больше времени корреляции шума:
является медленным нормальным случайным процессом, т. е. время корреляции сообщения много больше времени корреляции шума: 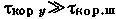 . Оптимальный нелинейный фильтр должен с наибольшей возможной точностью воспроизвести на выходе изменяющийся параметр
. Оптимальный нелинейный фильтр должен с наибольшей возможной точностью воспроизвести на выходе изменяющийся параметр 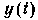 На рис. 7-79 приведен вариант структурной схемы оптимального нелинейного фильтра.
На рис. 7-79 приведен вариант структурной схемы оптимального нелинейного фильтра.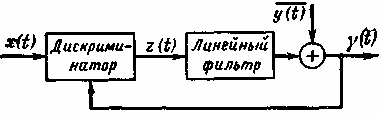
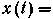
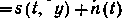 , а на выходе образуется измеренное значение сообщения (его оценка)
, а на выходе образуется измеренное значение сообщения (его оценка) 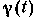 . В дискриминаторе, являющемся в общем случае элементом нелинейным, радиосигнал демодулируется, из него выделяется сопровождаемое шумом полезное сообщение
. В дискриминаторе, являющемся в общем случае элементом нелинейным, радиосигнал демодулируется, из него выделяется сопровождаемое шумом полезное сообщение 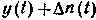 . Напряжение, соответствующее величине
. Напряжение, соответствующее величине 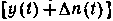 , сравнивается с напряжением, подводимым к дискриминатору с выхода фильтра по линии обратной связи. Физический смысл появления в схеме оптимального приемника обратной связи по воспроизводимому сообщению состоит в следующем. При малых значениях выходного напряжения характеристику дискриминатора можно считать линейной (для воспроизводимого сообщения). Поэтому для обеспечения неискаженного воспроизведения сообщения разность
, сравнивается с напряжением, подводимым к дискриминатору с выхода фильтра по линии обратной связи. Физический смысл появления в схеме оптимального приемника обратной связи по воспроизводимому сообщению состоит в следующем. При малых значениях выходного напряжения характеристику дискриминатора можно считать линейной (для воспроизводимого сообщения). Поэтому для обеспечения неискаженного воспроизведения сообщения разность 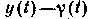 нужно поддерживать достаточно малой. Эту задачу и помогает решить линия обратной связи. В результате на выходе дискриминатора образуется напряжение
нужно поддерживать достаточно малой. Эту задачу и помогает решить линия обратной связи. В результате на выходе дискриминатора образуется напряжение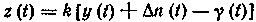 . (7-308)
. (7-308)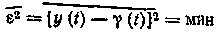
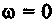 до некоторой граничной верхней частоты
до некоторой граничной верхней частоты 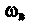 (рис. 3.48, а).
(рис. 3.48, а).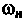 до бесконечности (рис. 3.48, б).
до бесконечности (рис. 3.48, б).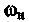 и граничной верхней часто той
и граничной верхней часто той 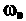 (рис. 3.48, в).
(рис. 3.48, в).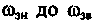 (рис. 3.48, г).
(рис. 3.48, г).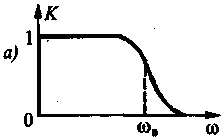
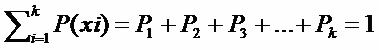
 . Однако использование числа N в качестве меры информации неудобно, так как в данном случае не выполняется условие пропорциональности между длиной слова (длительностью сигнала) и количеством содержащейся в нем информации. Между тем удвоение времени передачи сообщений должно приводить к удвоению количества передаваемой информации.
. Однако использование числа N в качестве меры информации неудобно, так как в данном случае не выполняется условие пропорциональности между длиной слова (длительностью сигнала) и количеством содержащейся в нем информации. Между тем удвоение времени передачи сообщений должно приводить к удвоению количества передаваемой информации.


