
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Навешивание кванторов на предикат.Содержание книги Поиск на нашем сайте Пусть Р(х) какой-нибудь предикат. Навешивание квантора всеобщности – это операция, которая сопоставляет предикату Р(х) высказывание «Для всякого х имеет место Р(х)». Для обозначения этой операции употребляется знак ". В словесных формулировках этот знак заменяет слова «все», «всякий», «любой», «каждый». Символическая запись операции имеет вид: Заметим, что высказывание Навешивание к вантора существования – это операция, которая предикату Р(х)сопоставляет высказывание «существует такое х, что имеет место Р(х)». Его символическая запись имеет вид Высказывание Знак существования $ употребляется вместо слов «хотя бы один», «найдется», «существует». Несмотря на то, что в записях формул ("х)Р(х) и ($х)Р(х) встречается буква х, обозначающая переменную, обе эти формулы обозначают высказывания: от переменной х они больше не зависят. Принято говорить, что в формулах ("х)Р(х) и ($х)Р(х) кванторы " и $ связывают переменную х. Навешивание квантора всеобщности есть обобщение операции конъюнкции на произвольное конечное или бесконечное множество членов конъюнкции (сомножителей). Навешивание квантора существования на предикат есть обобщение операции дизъюнкции на произвольное, конечное или бесконечное, множество членов дизъюнкции (слагаемых). Если предикат зависит от нескольких переменных, то навешивание одного квантора понижает число переменных на единицу. Чтобы получить из предиката высказывание, надо связать кванторами все его переменные. Например, из предиката Q (x, y): x > y, определенного на множестве пар действительных чисел, навешиванием кванторов можно получить 8 высказываний с соответствующими значениями истинности:
Этот пример показывает, что разноименные кванторы, вообще говоря, менять местами нельзя: при перестановке кванторов значение истинности получаемого высказывания меняется. Попытайтесь выяснить, в каком случае разноименные кванторы можно переставлять. Заметим, наконец, что между кванторами имеют место соотношения, позволяющие сводить один из этих кванторов к другому:
Задача. Записать высказывание, используя символы кванторов и предикатов, и построить его отрицание: В каждом городе, на каждой улице есть дом с балконом. Решение. Пусть P (x): x – город; Q (x, y): y – улица города x; R (z): z – дом с балконом, M (x, y, z): z - дом на улице y в городе x. Тогда формула высказывания имеет вид
Построим отрицание этой формулы:
Задачи 76. Какие из следующих выражений являются предикатами? а) Человек x – преступник. б) в) Человек x – адвокат человека y. г) a и b проходят подозреваемыми по делу № z. д) е) Иван и Марья – супруги. ж) 77. Определить множество истинности предиката, если
78. Даны предикаты a) d) 79. Записать множество истинности предиката
а) множестве натуральных чисел; b) множестве целых чисел; c) множестве рациональных чисел; d) множестве вещественных чисел. 80. Пусть имеются предикаты 1) 4) 7) 81. В аристотелевской логике рассматривалось четыре вида так называемых категорических суждений: 1. «Все S суть Р» – общеутвердительное суждение. 2. «Ни одно S не есть Р» – общеотрицательное суждение. 3. «Некоторые S суть Р» – частноутвердительное суждение. 4. «Некоторые S не суть Р» – частноотрицательное суждение. Пусть S – переменное, а P – фиксированное утверждение. Запишите данные схемы высказываний на языке логики предикатов. Постройте отрицания к ним. Решите эту же задачу для случая, когда и S, и P – переменные. 82. Используя предикаты Р (х) = { х – простое число}, S (x) = { х – четное число}, Q (x) = { х – отрицательное число}, R (x, y) = { х > y }, операции над ними и кванторы, запишите следующие высказывания: а) существует простое четное число, б) всякое простое число, большее двух, нечетно. в) не существует отрицательного числа, большего нуля; г) не существует простого четного числа, большего двух; 83. Сформулируйте следующие высказывания и укажите их значения истинности: а) (" х)($ у)(х + у = 4); б) ($ у)(" х) (х + у = 4); в) ($ х)($ у)(х + у = 4); г) (" х)(" у)(х + у = 4). 84. Пусть на множестве натуральных чисел определены следующие предикаты: Р (х) = { х – простое число}, R (x) = { х – четное число}, Q (х) = { х – нечетное число}, S (х, у) = { х делится на у }. Сформулируйте следующие утверждения: а) в) (" х)(S (x, 2)Þ R (x)); г) ($ х)(R (x) Ù S (x, 6)); д) ($ х)(Q (x) Ù P (x)); е) ж) з) (" х)((Р (х)Þ($ у)(R (y) Ù S (y, x))); и) 85. Даны следующие предикаты, определенные на множестве людей: А (х) = { х – преступник}, В (х) = { х – судья}, С (х) = { х – мужчина}; D (x) = { х – свидетель}; Е (х) = { х – соучастник}. Дайте словесную формулировку следующих утверждений: а) ($ х)(А (х) Ù С (х)); б) 86. Сформулируйтевысказывания, которые являются отрицаниями следующих: а) существует наибольшее простое число; б) любое вымогательство наказывается лишением свободы; в) в некотором поезде, идущем из Москвы в Ярославль, в каждом вагоне есть свободное место. г) каждый, совершивший преступление, должен быть подвергнут справедливому наказанию. д) ни один невиновный не должен быть привлечен к уголовной ответственности 87. Выразите следующие высказывания на языке логики предикатов. Постройте их отрицания и переведите их на русский язык. а) Все работники подлежат обязательному медицинскому страхованию. б) Все люди рождаются свободными и равными в своих достоинствах и правах. в) Некоторые люди освобождаются от уплаты судебных расходов в доход государства. г) Некоторые приговоры суда являются обвинительными. д) Ни один приговор суда не должен быть необоснованным. е) Существует книга, которую все прочитали. ж) Не все осужденные за совершение преступлений освобождаются по амнистии. з) Ни один образец производственного оборудования не может быть передан в серийное производство, если он не отвечает требованиям охраны труда. 88. Запишите с помощью логической символики высказывания: а) существует точно одно х, такое, что Ф (х); б) существует по крайней мере два х, таких, что Ф (х); в) существует не более двух х, таких, что Ф (х). г) два и только два х обладают свойством Ф. 89. Постройте отрицания следующих высказываний и дайте их словесную формулировку. а) (" х)(" у)((x > y)Ú (x < y) Ú (x = y)); б) в) 90. Предикаты Р (х) и Q (x) определены на некотором множестве Т. В каком отношении должны находиться области истинности 1) Р (х)Ù Q (x) принимал значение 1: а) для некоторых х Î в) для всех х Î 2) Р (х)Þ Q (x) принимал значение 1: а) для всех х Î Т, б) ни для одного значения х Î Т. 91. Почему высказывания в следующих парах не являются отрицаниями одно другого? Ответ обоснуйте на основе определения операции отрицания. а) Все преступления носят экономический характер. Все преступления не носят экономический характер. б) Некоторые юристы работают адвокатами. Некоторые юристы не работают адвокатами. 92. Придумайте два высказывания, имеющие соответственно форму а) оба они были истинными; б) оба были ложными; в) первое – ложным, а второе – истинным. 93. Даны предложения: «Каждую задачу решил, по крайней мере, один студент» и «По крайней мере, один студент решил каждую задачу». Имеют ли эти предложения один и тот же смысл? Следует ли хотя бы одно из них из другого? Почему? 94. Запишите символически следующие предложения и определите их значения истинности. а) Всякое число, умноженное на нуль, есть нуль. б) Произведение любого числа и единицы равно этому числу. в) Существует число, которое больше своего квадрата. г) Квадрат любого числа неотрицателен. д) Модуль любого числа положителен. 95. Запишите символически следующие предложения и определите их значения истинности. Укажите области определения предикатов: а) Существует рациональное число, квадрат которого равен 2; б) Всякое натуральное число либо четно, либо нечетно; в) Всякое рациональное число представимо в виде дроби г) Некоторые натуральные числа делятся на 7. Определите множества истинности предикатов, на которые навешиваются кванторы. Приведите, где это возможно, примеры чисел из множеств истинности. 96. Запишите символически: а) положительные оценки на всех экзаменах являются необходимым условием для перевода любого студента на следующий курс; б) в) функция 97. Сформулируйте следующие высказывания, используя квантор всеобщности: а) не существует такого числа x, что б) нет человека, не имеющего матери; в) не найдется студента, не сдавшего экзамена по уголовному праву и в то же время переведенного на следующий курс; г) ни один человек не бессмертен. 98. Сформулируйте отрицания следующих высказываний в утвердительной форме (то есть так, чтобы отрицание высказывания не начиналось со слов: «неверно, что» или «не»). а) Из всякого положения есть выход; б) В каждой стране найдется город, у всех жителей которого один и тот же цвет глаз; в) В каждом городе есть вуз, в котором есть факультет, где есть курс, в каждой группе которого ни один студент не занимается спортом. г) Существует книга, в которой есть страница, в каждой строке которой найдется хотя бы одна буква «а». 99. Запишите следующие высказывания в виде формул с кванторами, предварительно введя обозначения для используемых предикатов: 1) есть реки, которые впадают в Волгу; 2) Не все то золото, что блестит; 3) Всякий кулик свое болото хвалит; 4) Не всякий человек может добиться осуществления своей мечты; 5) Каждый студент-физик выполнил хотя бы одну лабораторную работу. 100. Пусть даны предикаты: М(x) – «x – мужчина»; V(x) – «x – женщина»; I(x, y) –«человек x моложе, чем y); K(x, y) – «x есть ребенок y); G(x, y) – «x состоит в браке с y); U(x) – «x живет в Ярославле»; A(x) – «x живет в Архангельске». Запишите в символической форме следующие предложения. 1) каждый человек имеет отца и мать; 2) каждый, кто имеет отца, имеет и мать; 3) всякий человек моложе своих родителей; 4) не всякий человек состоит в браке; 5) каждый человек моложе своего деда; 6) существует мужчина, у которого сын женат на женщине младше себя; 7) если в Ярославле есть женщина, имеющая брата в Архангельске, то в Архангельске есть мужчина, имеющий сестру в Ярославле. 8) не всякий женатый мужчина проживает в Архангельске. 101. Среди следующих предложений найдите пары высказываний, являющихся отрицаниями друг друга. 1) Все ученики нашей группы подготовились к семинару по уголовному праву. 2) Некоторые ученики нашей группы подготовились к семинару по уголовному праву. 3) Ни один ученик нашей группы не подготовился к семинару по уголовному праву. 4) Некоторые ученики нашей группы не подготовились к семинару по уголовному праву.
|
||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 4827; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.007 с.) |

 .
. .
. истинно. Отсюда следует, что
истинно. Отсюда следует, что  .
.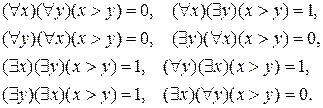

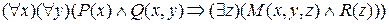 .
.
 .
. .
. .
. | х есть четное число},
| х есть четное число},  .
. и
и  . Найти множество истинности следующих предикатов
. Найти множество истинности следующих предикатов b)
b) 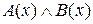 ; c)
; c)  ;
; ; e)
; e)  ; f)
; f)  .
. определенного на:
определенного на: и
и  . Изобразите в виде кругов Эйлера их множества истинности, затем изобразите множества истинности следующих предикатов:
. Изобразите в виде кругов Эйлера их множества истинности, затем изобразите множества истинности следующих предикатов: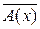 ; 2)
; 2) 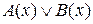 ; 3)
; 3)  ; 5)
; 5)  ; 6)
; 6)  ; 8)
; 8) 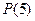 ; б) R (2)Ù P (2);
; б) R (2)Ù P (2);


 );
);
 .
. ; в)
; в) 

 ;
; .
. данных предикатов, чтобы предикат
данных предикатов, чтобы предикат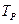 , б) для всех х Î
, б) для всех х Î  , г) ни для одного значения х Î Т.
, г) ни для одного значения х Î Т. и
и  , так чтобы:
, так чтобы: , где p – целое число, а q - натуральное число;
, где p – целое число, а q - натуральное число; имеет смысл при любых значениях x и y;
имеет смысл при любых значениях x и y; принимает любое неотрицательное значение.
принимает любое неотрицательное значение. ;
;


