
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи синтеза и анализа контактных схемСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Контактная схема является устройством из контактов и проводов, связывающих несколько полюсов (входов, выходов). Высказывания и электрические контакты – объекты совершенно разной природы, но между ними все-таки есть сходство. Высказывания могут принимать только два значения (0, 1), а электрические контакты могут находиться только в двух состояниях («замкнуто», «разомкнуто»). Это сходство служит основой для применения алгебры высказываний к задачам синтеза и анализа схем, и, наоборот, для моделирования формул алгебры высказываний схемами. Идея о возможности такого применения была высказана еще в 1910 году физиком П. Эренфестом. Однако строгое доказательство возможности и методика применения алгебры высказываний к синтезу и анализу электрических цепей впервые были разработаны в 30-ых годах советским ученым В.И. Шестаковым и американским ученым К.Э. Шенноном. Под синтезом схемы понимают конструирование схемы по заданным условиям ее работы (замыкания и размыкания), то есть на основе указания состояния контактов, при котором схема работает. Под анализом схемы понимают обратную задачу: определение условий работы заданной схемы по ее виду. Попутно с этими задачами возникает третья задача – упрощение схемы, то есть конструирование эквивалентной схемы, то есть схемы, работающей при тех же условиях, при которых работает исходная схема, но с меньшим числом контактов. Для установления соответствия между формулами алгебры высказываний и контактными схемами составим следующий словарь.
Посмотрим теперь, какие схемы соответствуют основным операциям алгебры высказываний: дизъюнкции, конъюнкции и отрицанию. Дизъюнкции Конъюнкции
Схема, соответствующая  , состоит из контакта , состоит из контакта  , называемого инверсией контакта а и управляемого тем же элементом (реле, выключателем), что и а. Это, по существу, означает, что а и , называемого инверсией контакта а и управляемого тем же элементом (реле, выключателем), что и а. Это, по существу, означает, что а и  – это два контакта, находящиеся всегда в противоположных состояниях: когда один замкнут, второй – разомкнут. – это два контакта, находящиеся всегда в противоположных состояниях: когда один замкнут, второй – разомкнут.
Так как каждая формула алгебры высказываний может быть выражена с помощью операций конъюнкции, дизъюнкции и отрицания, то каждой формуле алгебры высказываний можно поставить в соответствие контактную схему, составленную из контактов и их инверсий с помощью последовательных и параллельных соединений. Соответствие между формулами алгебры высказываний и контактными схемами является взаимно однозначным и обладает тем свойством, что переводит равносильные формулы алгебры высказываний в эквивалентные схемы, то есть схемы, которые при любых наборах положений входящих в них контактов принимают одинаковые состояния. Задачи 65. Найти формулы, которые представляют следующие контактные схемы:
а– «элемент
Замкнута ли цепь, если а) высказывание a Ú (b1 б) высказывание Решение. а) Нет. Если а истинно, то элемент k вышел из строя и тока нет. Если b1 б) Ток проходит по цепи, так как элемент k и, по крайней мере, один из элементов l1, l2, l3 находятся в рабочем состоянии. Проверьте, что высказывание (б) есть отрицание высказывания (а) самостоятельно. 67. Составьте контактные схемы для следующих логических функций 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 68. Составьте контактную схему из контактов a, b, c и их инверсий так, чтобы она была замкнутой тогда и только тогда, когда: а) замкнуты только два из трех контактов a, b, c; б) замкнуты не более двух из трех контактов a, b, c; в) замкнуты не менее двух из трех контактов a, b, c. 69. Упростите схемы:
70.
71. Функция f(x,y,z) задана таблицей. Построить контактную схему, представляющую данную функцию
а) б)
72. Машина-экзаменатор дает сигнал «зачет» в том и только в том случае, если экзаменующийся правильно ответил хотя бы на два из трех вопросов билета. При вводе в машину правильного ответа замыкается контакт в цепи сигнальной лампочки. Постройте схему этой цепи. 73. Постройте схему, позволяющую включать и выключать в комнате верхний свет любым из трех выключателей, один из которых находится при входе в комнату, другой – над письменным столом, третий – над диваном. 74. Комитет, состоящий из трех человек, включая председателя, выносит решение большинством голосов. Однако решение не может быть принято, если за него не проголосовал председатель. Голосование “за” производится нажатием кнопки, замыкающей контакт, и в случае принятия решения зажигается лампочка. Постройте простейшую схему такой цепи. 75. Прибор состоит из двух блоков. Первый блок состоит из четырех одинаковых деталей и работает при исправности хотя бы двух из них. Второй блок состоит из пяти одинаковых деталей и работает при исправности хотя бы трех из них. Весь прибор работает, если работают оба блока. Составить контактную схему, реализующую работу прибора.
Предикаты
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 721; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.008 с.) |

 соответствует схема, составленная из контактов а и b так, что она замкнута тогда и только тогда, когда замкнут хотя бы один из контактов, то есть схема, состоящая из параллельного соединения контактов.
соответствует схема, составленная из контактов а и b так, что она замкнута тогда и только тогда, когда замкнут хотя бы один из контактов, то есть схема, состоящая из параллельного соединения контактов. соответствует схема, составленная из контактов а и b так, что она замкнута тогда и только тогда, когда замкнуты оба контакта, то есть схема, состоящая из последовательного соединения контактов.
соответствует схема, составленная из контактов а и b так, что она замкнута тогда и только тогда, когда замкнуты оба контакта, то есть схема, состоящая из последовательного соединения контактов.



 а) б) в)
а) б) в)

 г) д) е)
г) д) е) 66. Электрическая цепь между точками М и
66. Электрическая цепь между точками М и  составлена по схеме, изображенной на рисунке. Рассмотрим высказывания:
составлена по схеме, изображенной на рисунке. Рассмотрим высказывания: цепи вышел из строя»,
цепи вышел из строя», – «элемент
– «элемент  цепи вышел из строя».
цепи вышел из строя». b2
b2 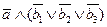
 истинно? Является ли одно из этих высказываний отрицанием другого?
истинно? Является ли одно из этих высказываний отрицанием другого?
 ;
; ;
;
 ;
; ;
; );
); ;
;


 ;
;



 ;
;
 ;
; ;
;
 ;
; ).
).
 а) б)
а) б)
 в) г)
в) г) Упростите схемы:
Упростите схемы: а) б)
а) б)


