Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формулы алгебры высказываний.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Определение 6. Формулами алгебры высказываний являются: 1) элементарные формулы, обозначающие элементарные высказывания: a, b, c, …, x, y, 0, 1; 2) если Формула алгебры высказываний принимает одно из двух значений (0 или 1) в соответствии со значениями образующих ее элементарных высказываний. Если рассматривать последние как независимые переменные, то формуле сопоставляется некоторая функция. Такая функция называется двузначной: ее области определения и значений составляют пару {0, 1}. Определение 7. Две формулы алгебры высказываний A и B называются равносильными, если на любом наборе входящих в них переменных они принимают одинаковое значение истинности. Для обозначения равносильности формул используется символ При записи формул скобки опускаются, если внутри них стоит знак конъюнкции (вместо Основные законы равносильности. 1) 2) 3) 4) дистрибутивные законы; 5) 6) третьего и закон противоречия; 7) 8) 9) 10) Нормальные формы. Элементарной дизъюнкцией называется дизъюнкция, состоящая только из переменных или их отрицаний. Примерами элементарных дизъюнкций служат формулы: Конъюнктивной нормальной формой (КНФ ) формулы алгебры высказываний называется ее запись в виде конъюнкции элементарных дизъюнкций. Элементарной конъюнкцией называется конъюнкция, состоящая только из переменных или их отрицаний, например: Дизъюнктивной нормальной формой (ДНФ) формулы алгебры высказываний называется ее запись виде дизъюнкции элементарных конъюнкций. Совершенной конъюнктивной нормальной формой формулы алгебры высказываний (СКНФ) называется КНФ, которая удовлетворяет следующим условиям: – все элементарные дизъюнкции, входящие в КНФ, различны, – нет нулевых дизъюнкций, – ни одна из элементарных дизъюнкций не содержит одинаковых членов, – каждая элементарная дизъюнкция содержит все переменные, входящие в формулу. Совершенной дизъюнктивной нормальной формой формулы алгебры высказываний (СДНФ) называется ДНФ, которая удовлетворяет следующим условиям: – все элементарные конъюнкции, составляющие ее, различны; – она не содержит нулевых конъюнкций; – ни одна из элементарных конъюнкций не содержит одинаковых членов; – каждая элементарная конъюнкция содержит все переменные, входящие в формулу. Чтобы получить СДНФ (СКНФ), надо сначала найти ДНФ (КНФ). Тогда будут выполнены условия 1, 2, 3. После этого надо преобразовать эту ДНФ (КНФ) таким образом, чтобы было выполнено условие 4, и вновь проверить выполнение условия 1. Задачи 1. Какие из перечисленных ниже предложений являются в математической логике высказываниями и каково значение их истинности? 1. Суд принимает только те из предоставляемых доказательств, которые имеют значение для дела. 2. Число 3. Хищение не является преступлением. 4. Некоторые приговоры суда являются обвинительными. 5. Картины Пикассо слишком абстрактны. 2. Обозначим высказывание: «Федоров юрист» символом а, а высказывание «Федоров – следователь прокуратуры» – символом b. Дайте словесную формулировку следующим формулам: 1) 4) а Þ b, 5) b Þ a, 6) ` а Þ` b, 7)` b Þ` a, 8)` a Ú b, 9) 3. Пусть символы с, r, s, p обозначают соответственно высказывания: «сегодня ясно», «сегодня дождь», «сегодня идет снег», «вчера было пасмурно». Прочитайте словесно следующие формулы: 1) 4. Переведите на язык алгебры высказываний следующие предложения (в каждом предложении элементарные высказывания должны быть обозначены одним символом): 1. Если светит солнце, то для того, чтобы не было дождя, достаточно, чтобы дул ветер. 2. Неверно, что если дует ветер, то солнце светит только тогда, когда нет дождя. 3. Чтобы погода была солнечной, достаточно, чтобы не было ни дождя, ни ветра. 4. Если ветра нет, то для дождя необходима пасмурная погода. 5. Если погода пасмурная и дует ветер, то дождя нет, но дождь идет. Значит, ветра нет. 6. Неверно, что если погода пасмурная, то дождь идет тогда и только тогда, когда нет ветра. 7. Если для солнечной погоды необходимо отсутствие дождя, то для того, чтобы пошел дождь, достаточно, чтобы погода была пасмурной и безветренной. 8. Будет ветреная погода, и пойдет дождь. 9. Дождь идет только тогда, когда погода пасмурная и безветренная. Но дождя нет. Значит, погода либо солнечная, либо пасмурная и ветреная. 10. Погода не только солнечная, но и безветренная. Значит, если не поднимется ветер, то дождя не будет. 11.Погода будет не только пасмурной, но и дождливой, несмотря на ветер. Значит, солнечной погоды не будет, но дождь прекратиться. 5. Запишите формулами следующие сложные высказывания: а) Студент только тогда переводится на следующий курс, когда успевает по всем дисциплинам. б) Судебное следствие признается неполным, если по делу не установлены с достаточной полнотой данные о личности обвиняемого. в) Для того, чтобы сумма чисел делилась на 3, достаточно, чтобы каждое слагаемое делилось на 3. г) Для того, чтобы суд пришел к выводу о подложности документа, необходимо, чтобы он устранил его из числа доказательств. д) Достаточным условием заявления судьи о самоотводе является его заинтересованность в деле. е) Утрата стороной дееспособности не является достаточным условием приостановления производства по делу. 6. Составьте формулы следующих высказываний: 1. Если Ильин достигнет четырнадцати лет и совершит убийство, то он будет нести уголовную ответственность; если же он не совершит убийство, то он не будет нести уголовную ответственность. 2. Николаев будет нести уголовную ответственность по ст.158 тогда и только тогда, когда совершит кражу; если Николаев не будет нести уголовную ответственность по ст.158, то его жена не подаст на развод и поможет ему устроиться на работу. 3. Если меняется характер собственности в стране, то неизбежно меняются взаимоотношения профсоюзов с администрацией предприятий, а меняются эти взаимоотношения, то неизбежно должны меняться содержание деятельности профсоюзов, их организационное строение, формы и методы работы. 7. Для каждой из следующих формул придумайте два формализуемых ею предложения: 1) 8. На допросе свидетель А сказал, что В говорит неправду. Следователь рассуждает так: «Свидетель А может говорить правду и тогда В говорит неправду, или свидетель А говорит неправду и тогда В говорит правду». Как записать рассуждение следователя в виде формулы? 9. На допросе А сказал, что В говорит неправду, а В сказал, что С говорит неправду. Следователь рассуждает так: «Свидетель А может говорить правду и тогда В говорит неправду, или свидетель А говорит неправду и тогда В говорит правду, а С говорит неправду, или свидетель В говорит неправду, и тогда С говорит правду». Как записать рассуждение в виде логической формулы? 10. Запишите следующее предложение в виде формулы: «Если будет хорошая погода, то мы пойдем на речку и будем купаться или поедем в лес и будем собирать грибы». Запишите отрицание полученной формулы и отнесите знак отрицания к элементарным высказываниям. Решение. Обозначим высказывания «будет хорошая погода», «мы пойдем на речку», «мы будем купаться», «поедем в лес», «будем собирать грибы» соответственно символами а, b, с, d, е. Тогда данное высказывание запишется следующим образом:
11. Сформулируйте следующие предложения, используя слова «необходимо», «достаточно», «тогда, когда» и «только тогда, когда»: а) Если со дня совершения тяжкого преступления прошло десять лет, то лицо освобождается от уголовной ответственности. б) Если студент учится на юридическом факультете, то он изучает математику. Указание: Высказывание «Если а, то b» равносильно следующим высказываниям: «Для b достаточно а», «Для а необходимо b», «b тогда, когда а», «а только тогда, когда b». 12. Известно, что конъюнкция 13. Известно, что дизъюнкция 14. Что можно сказать про истинность импликации a Þ b, если: 1) а º 1? 2) b º 1? 3) a º 0? 4) b º 0? 5) а – «5<8», b – «Потерпевший вправе заявить ходатайство»? 6) а – «кража – преступление», b – «Путин – президент США». 15. «Это, конечно, Сова. Или я не Вини-Пух. А я – он …» (А. А. Милн «Вини-Пух»). Рассмотрите высказывание: «Если это не Сова, то я не Вини-Пух». Покажите, что рассуждение Вини-Пуха логически грамотно. 16. Запишите высказывание формулой и составьте для нее таблицу истинности: «Если завтра не будет дождя, мы отправимся на реку или пойдем в лес». Что мы будем делать завтра, если данное высказывание ложно? Решение. Обозначим через а высказывание «завтра будет дождь», через b –высказывание «мы пойдем на реку», через с – высказывание «мы пойдем в лес». Тогда данное высказывание запишется в виде формулы:` a Þ (b Ú c). Таблица истинности этой формулы имеет вид:
Высказывание ложно в единственном случае (см. последнюю строку таблицы). Из этой строки заключаем, что «завтра дождя не будет, но ни на реку, ни в лес мы не пойдем». 17. Постройте таблицы истинности для следующих формул: 1) 5) 9) 11) 18. Составьте таблицы истинности для следующих формул: а) 19. Докажите с помощью таблиц истинности законы де Моргана: 1) 20. С помощью таблиц истинности докажите равносильность следующих формул: 1) 21. Проверьте, будут ли равносильны следующие формулы: 1) 3) 22. Упростите следующие формулы алгебры высказываний: а) в) Решение. а) 23. Проверьте равносильность формул с помощью преобразований: а) б) в) г) д) е) 24. Докажите равносильность формул алгебры высказываний двумя способами.
Следующая группа задач иллюстрирует теорему: Каждую двузначную функцию Напомним, что двузначной функцией называется функция,у которой и переменные, и сама она принимают только два значения:1 и 0. Двузначные функции называют также булевыми функциями. 25. Проверьте, будут ли булевыми следующие арифметические функции 1) Решение. 1) Составим таблицу значений функции
Среди значений функции есть значение –1, следовательно, эта функция не является булевой. 26. Запишите в виде формулы алгебры высказываний следующие арифметические функции от двоичных аргументов: а) в) д) ж) и) Решение. ж) Сначала составим таблицу значений функции
Функция является булевой, и ее можно реализовать в виде формулы алгебры высказываний. Теперь, используя таблицу, составим СДНФ соответствующей формулы алгебры высказываний и упростим ее:
27. По формуле алгебры высказываний найти соответствующую ей двузначную арифметическую функцию: 1)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 1128; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.011 с.) |

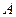 и
и 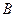 – формулы, то
– формулы, то 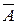 ,
,  ,
,  ,
,  ,
,  также являются формулами алгебры высказываний.
также являются формулами алгебры высказываний. :
:  .
. пишут
пишут  ), порядок действий при вычислениях по формуле принят следующий:1) отрицание, 2) конъюнкция, 3) дизъюнкция, 4) импликация, 5) эквиваленция.
), порядок действий при вычислениях по формуле принят следующий:1) отрицание, 2) конъюнкция, 3) дизъюнкция, 4) импликация, 5) эквиваленция. ,
, 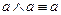 – законы идемпотентности;
– законы идемпотентности; ,
, 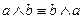 – законы коммутативности;
– законы коммутативности; ,
,  – законы ассоциативности;
– законы ассоциативности; ,
,  –
– ,
, 
 – законы де Моргана;
– законы де Моргана; ,
,  – закон исключенного
– закон исключенного ,
,  – законы поглощения 0 и 1;
– законы поглощения 0 и 1;
 – закон двойного отрицания;
– закон двойного отрицания; ;
;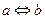 º (
º ( ).
). ,
,  .
.


 .
. не превосходит число7.
не превосходит число7. , 2)
, 2)  , 3) a
, 3) a  .
.
 , 2)
, 2)  , 3)
, 3)  , 4)
, 4) 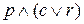 , 5)
, 5) 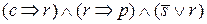 .
. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
. . Построим его отрицание:
. Построим его отрицание: .
. истинна. Что можно сказать о значении истинности высказываний a, b и c?
истинна. Что можно сказать о значении истинности высказываний a, b и c? ложна. Что можно сказать о значении истинности самих высказываний a, b и c?
ложна. Что можно сказать о значении истинности самих высказываний a, b и c?



 ; 2)
; 2)  ; 3)
; 3) 


 ;
; ; 6) (
; 6) (
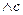 ; 7)
; 7) 
 ;
; 10)
10) 
 ; 12)
; 12) 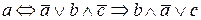 .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. ; 2)
; 2)  .
. ); 2)
); 2)  .
. и
и  ; 2)
; 2)  и
и  ;
; и
и  .
. ; б)
; б)  ;
; .
. .
. ;
;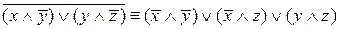 ;
;
 ;
;



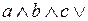
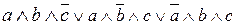 и
и  .
. ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
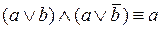 ;
;
 ;
;
 ;
;
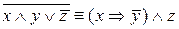 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
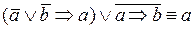 ;
;
 ;
;

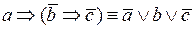 ;
;

 ;
;
 от n переменных можно представить в виде формулы алгебры высказываний.
от n переменных можно представить в виде формулы алгебры высказываний. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  , где n, m, k,r – любыt натуральные числа.
, где n, m, k,r – любыt натуральные числа.
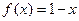 ; б)
; б)  ;
; ; г)
; г)  ;
; ; е)
; е)  ;
; ;з)
;з) 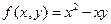 ;
; .
.
 .
. ; 2)
; 2) 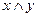 ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  ; 6)
; 6)