
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы математической логики.Содержание книги Поиск на нашем сайте
Элементы математической логики. Формулы алгебры высказываний Высказывания и операции над ними. Под высказыванием понимают повествовательное предложение, о котором имеет смысл говорить, что оно истинно или ложно. Высказываниями не являются определения, вопросительные и восклицательные предложения, а также субъективные суждения. Высказывания обозначают малыми буквами латинского алфавита. В математической логике отвлекаются от содержательной стороны высказываний, ограничиваясь рассмотрением их значений истинности (истинностных значений). Если высказывание а истинно, то ему приписывают истинностное значение И (или 1) и пишут [ а ] = И или [a] = 1, а если ложно – истинностное значение Л (или 0) и пишут [ а ]=Л или [a] = 0. Никакое высказывание не может быть одновременно и истинным, и ложным. Под элементарным (или простым) понимают высказывание, рассматриваемое как целое, неразложимое на составные части предложение, внутренняя структура которого нас не интересует. Также как составное повествовательное предложение можно образовать с помощью ряда связок из простых предложений, так и составное (или сложное) высказывание можно получить из элементарных, применяя к ним логические операции. Пусть а и b - произвольные высказывания, относительно которых мы не предполагаем, что известны их истинностные значения. Определение 1. Отрицанием высказывания а называется такое высказывание Для пояснения логических операций удобно использовать так называемые таблицы истинности (истинностные таблицы). Таблица, иллюстрирующая определение 1, имеет вид:
Определение 2. Конъюнкцией высказываний Истинностная таблица для конъюнкции имеет вид:
Вместо знака Определение 3. Дизьюнкцией высказываний а и b называется высказывание
Союз «или» в данном случае носит неразделительный смысл, поскольку высказывание Дизъюнкции соответствует следующая таблица истинности:
Определение 4. Импликацией высказываний а и b называется высказывание Истинностная таблица для импликации такова:
В импликации Грамматическими выражениями импликации, помимо предложений «если а, то b», «из а следует b», «а влечет b», «а имплицирует b», могут служить и другие словосочетания: «b выполняетсяпри условии, что выполняется а», «b выполняется тогда, когда выполняется а», «а выполняется только тогда, когда выполняется b», «b есть необходимое условие для а», «а есть достаточное условие для b», «в случае а имеет место b». Определение 5. Эквиваленцией высказываний а и b называется высказывание Таблица истинности для эквиваленции имеет вид:
Основные законы равносильности. 1) 2) 3) 4) дистрибутивные законы; 5) 6) третьего и закон противоречия; 7) 8) 9) 10) Нормальные формы. Элементарной дизъюнкцией называется дизъюнкция, состоящая только из переменных или их отрицаний. Примерами элементарных дизъюнкций служат формулы: Конъюнктивной нормальной формой (КНФ ) формулы алгебры высказываний называется ее запись в виде конъюнкции элементарных дизъюнкций. Элементарной конъюнкцией называется конъюнкция, состоящая только из переменных или их отрицаний, например:
Дизъюнктивной нормальной формой (ДНФ) формулы алгебры высказываний называется ее запись виде дизъюнкции элементарных конъюнкций. Совершенной конъюнктивной нормальной формой формулы алгебры высказываний (СКНФ) называется КНФ, которая удовлетворяет следующим условиям: – все элементарные дизъюнкции, входящие в КНФ, различны, – нет нулевых дизъюнкций, – ни одна из элементарных дизъюнкций не содержит одинаковых членов, – каждая элементарная дизъюнкция содержит все переменные, входящие в формулу. Совершенной дизъюнктивной нормальной формой формулы алгебры высказываний (СДНФ) называется ДНФ, которая удовлетворяет следующим условиям: – все элементарные конъюнкции, составляющие ее, различны; – она не содержит нулевых конъюнкций; – ни одна из элементарных конъюнкций не содержит одинаковых членов; – каждая элементарная конъюнкция содержит все переменные, входящие в формулу. Чтобы получить СДНФ (СКНФ), надо сначала найти ДНФ (КНФ). Тогда будут выполнены условия 1, 2, 3. После этого надо преобразовать эту ДНФ (КНФ) таким образом, чтобы было выполнено условие 4, и вновь проверить выполнение условия 1. Задачи 1. Какие из перечисленных ниже предложений являются в математической логике высказываниями и каково значение их истинности? 1. Суд принимает только те из предоставляемых доказательств, которые имеют значение для дела. 2. Число 3. Хищение не является преступлением. 4. Некоторые приговоры суда являются обвинительными. 5. Картины Пикассо слишком абстрактны. 2. Обозначим высказывание: «Федоров юрист» символом а, а высказывание «Федоров – следователь прокуратуры» – символом b. Дайте словесную формулировку следующим формулам: 1) 4) а Þ b, 5) b Þ a, 6) ` а Þ` b, 7)` b Þ` a, 8)` a Ú b, 9) 3. Пусть символы с, r, s, p обозначают соответственно высказывания: «сегодня ясно», «сегодня дождь», «сегодня идет снег», «вчера было пасмурно». Прочитайте словесно следующие формулы: 1) 4. Переведите на язык алгебры высказываний следующие предложения (в каждом предложении элементарные высказывания должны быть обозначены одним символом): 1. Если светит солнце, то для того, чтобы не было дождя, достаточно, чтобы дул ветер. 2. Неверно, что если дует ветер, то солнце светит только тогда, когда нет дождя. 3. Чтобы погода была солнечной, достаточно, чтобы не было ни дождя, ни ветра. 4. Если ветра нет, то для дождя необходима пасмурная погода. 5. Если погода пасмурная и дует ветер, то дождя нет, но дождь идет. Значит, ветра нет. 6. Неверно, что если погода пасмурная, то дождь идет тогда и только тогда, когда нет ветра. 7. Если для солнечной погоды необходимо отсутствие дождя, то для того, чтобы пошел дождь, достаточно, чтобы погода была пасмурной и безветренной. 8. Будет ветреная погода, и пойдет дождь. 9. Дождь идет только тогда, когда погода пасмурная и безветренная. Но дождя нет. Значит, погода либо солнечная, либо пасмурная и ветреная. 10. Погода не только солнечная, но и безветренная. Значит, если не поднимется ветер, то дождя не будет. 11.Погода будет не только пасмурной, но и дождливой, несмотря на ветер. Значит, солнечной погоды не будет, но дождь прекратиться. 5. Запишите формулами следующие сложные высказывания: а) Студент только тогда переводится на следующий курс, когда успевает по всем дисциплинам.
б) Судебное следствие признается неполным, если по делу не установлены с достаточной полнотой данные о личности обвиняемого. в) Для того, чтобы сумма чисел делилась на 3, достаточно, чтобы каждое слагаемое делилось на 3. г) Для того, чтобы суд пришел к выводу о подложности документа, необходимо, чтобы он устранил его из числа доказательств. д) Достаточным условием заявления судьи о самоотводе является его заинтересованность в деле. е) Утрата стороной дееспособности не является достаточным условием приостановления производства по делу. 6. Составьте формулы следующих высказываний: 1. Если Ильин достигнет четырнадцати лет и совершит убийство, то он будет нести уголовную ответственность; если же он не совершит убийство, то он не будет нести уголовную ответственность. 2. Николаев будет нести уголовную ответственность по ст.158 тогда и только тогда, когда совершит кражу; если Николаев не будет нести уголовную ответственность по ст.158, то его жена не подаст на развод и поможет ему устроиться на работу. 3. Если меняется характер собственности в стране, то неизбежно меняются взаимоотношения профсоюзов с администрацией предприятий, а меняются эти взаимоотношения, то неизбежно должны меняться содержание деятельности профсоюзов, их организационное строение, формы и методы работы. 7. Для каждой из следующих формул придумайте два формализуемых ею предложения: 1) 8. На допросе свидетель А сказал, что В говорит неправду. Следователь рассуждает так: «Свидетель А может говорить правду и тогда В говорит неправду, или свидетель А говорит неправду и тогда В говорит правду». Как записать рассуждение следователя в виде формулы? 9. На допросе А сказал, что В говорит неправду, а В сказал, что С говорит неправду. Следователь рассуждает так: «Свидетель А может говорить правду и тогда В говорит неправду, или свидетель А говорит неправду и тогда В говорит правду, а С говорит неправду, или свидетель В говорит неправду, и тогда С говорит правду». Как записать рассуждение в виде логической формулы? 10. Запишите следующее предложение в виде формулы: «Если будет хорошая погода, то мы пойдем на речку и будем купаться или поедем в лес и будем собирать грибы». Запишите отрицание полученной формулы и отнесите знак отрицания к элементарным высказываниям. Решение. Обозначим высказывания «будет хорошая погода», «мы пойдем на речку», «мы будем купаться», «поедем в лес», «будем собирать грибы» соответственно символами а, b, с, d, е. Тогда данное высказывание запишется следующим образом:
11. Сформулируйте следующие предложения, используя слова «необходимо», «достаточно», «тогда, когда» и «только тогда, когда»: а) Если со дня совершения тяжкого преступления прошло десять лет, то лицо освобождается от уголовной ответственности. б) Если студент учится на юридическом факультете, то он изучает математику. Указание: Высказывание «Если а, то b» равносильно следующим высказываниям: «Для b достаточно а», «Для а необходимо b», «b тогда, когда а», «а только тогда, когда b». 12. Известно, что конъюнкция 13. Известно, что дизъюнкция 14. Что можно сказать про истинность импликации a Þ b, если: 1) а º 1? 2) b º 1? 3) a º 0? 4) b º 0? 5) а – «5<8», b – «Потерпевший вправе заявить ходатайство»? 6) а – «кража – преступление», b – «Путин – президент США». 15. «Это, конечно, Сова. Или я не Вини-Пух. А я – он …» (А. А. Милн «Вини-Пух»). Рассмотрите высказывание: «Если это не Сова, то я не Вини-Пух». Покажите, что рассуждение Вини-Пуха логически грамотно. 16. Запишите высказывание формулой и составьте для нее таблицу истинности: «Если завтра не будет дождя, мы отправимся на реку или пойдем в лес». Что мы будем делать завтра, если данное высказывание ложно? Решение. Обозначим через а высказывание «завтра будет дождь», через b –высказывание «мы пойдем на реку», через с – высказывание «мы пойдем в лес». Тогда данное высказывание запишется в виде формулы:` a Þ (b Ú c). Таблица истинности этой формулы имеет вид:
Высказывание ложно в единственном случае (см. последнюю строку таблицы). Из этой строки заключаем, что «завтра дождя не будет, но ни на реку, ни в лес мы не пойдем». 17. Постройте таблицы истинности для следующих формул: 1) 5) 9) 11) 18. Составьте таблицы истинности для следующих формул: а) 19. Докажите с помощью таблиц истинности законы де Моргана: 1) 20. С помощью таблиц истинности докажите равносильность следующих формул: 1) 21. Проверьте, будут ли равносильны следующие формулы: 1) 3) 22. Упростите следующие формулы алгебры высказываний: а) в) Решение. а) 23. Проверьте равносильность формул с помощью преобразований: а) б) в) г) д) е) 24. Докажите равносильность формул алгебры высказываний двумя способами.
Следующая группа задач иллюстрирует теорему: Каждую двузначную функцию Напомним, что двузначной функцией называется функция,у которой и переменные, и сама она принимают только два значения:1 и 0. Двузначные функции называют также булевыми функциями. 25. Проверьте, будут ли булевыми следующие арифметические функции
1) Решение. 1) Составим таблицу значений функции
Среди значений функции есть значение –1, следовательно, эта функция не является булевой. 26. Запишите в виде формулы алгебры высказываний следующие арифметические функции от двоичных аргументов: а) в) д) ж) и) Решение. ж) Сначала составим таблицу значений функции
Функция является булевой, и ее можно реализовать в виде формулы алгебры высказываний. Теперь, используя таблицу, составим СДНФ соответствующей формулы алгебры высказываний и упростим ее:
27. По формуле алгебры высказываний найти соответствующую ей двузначную арифметическую функцию: 1)
Решение логических задач Под логическими задачами обычно понимают такие задачи, которые решаются с помощью одних только логических операций, с использованием аппарата алгебры высказываний. При этом возникают трудности, связанные с переводом задач на язык алгебры высказываний и с использованием аппарата этой алгебры. Логические задачи могут решаться и фактически решаются обычными рассуждениями, иногда довольно длинными. Поэтому удобно использовать «комбинированный» метод, который состоит в том, что обычные рассуждения сочетаются с переводом условий задач на язык алгебры высказываний или со специально составленными таблицами, схемами. Задачи 33. Однажды следователю пришлось одновременно допрашивать трех свидетелей: Клода, Жака и Дика. Их показания противоречили друг другу, и каждый из них обвинял кого-нибудь во лжи. Клод утверждал, что Жак лжет, Жак обвинял во лжи Дика, а Дик уговаривал следователя не верить ни Клоду, ни Жаку. Но следователь быстро вывел их на чистую воду, не задав им ни одного вопроса. Кто из свидетелей говорил правду? Решение. Обозначим показания свидетелей Клода, Жака и Дика соответственно буквами К, Ж, Д. Мы не знаем, какие показания истинны, а какие ложны, но нам известно следующее: 1) либо Клод сказал правду, и тогда Жак солгал, либо Клод солгал, и тогда Жак сказал правду; 2) либо Жак сказал правду, и тогда Дик солгал, либо Жак солгал, и тогда Дик сказал правду; 3) либо Дик сказал правду, и тогда Клод и Жак солгали, либо Дик солгал, и тогда неверно, что оба других свидетеля солгали. Каждое из этих трех высказываний является истинным, для каждого из них составим формулу алгебры высказываний: 1) К Ù 2) Ж Ù 3) Д Ù Так как эти три формулы истинны одновременно, то истинна и их конъюнкция: (К Ù В левой части уравнения выполним конъюнкцию, используя дистрибутивный закон и отбрасывая те слагаемые, в которых какое-либо высказывание умножается на свое отрицание, а также заменяя два одинаковых сомножителя одним таким сомножителем: ( ( Теперь наше уравнение равносильно совсем простому уравнению: ( 34. После родительского собрания к учителю подошел один из родителей: «Вы не назвали моего сына среди хороших учеников. А ведь мой Федя – отличник и к тому же лучший лыжник класса». «Да, Вы правы» – ответил учитель, – «но хорошим учеником мы считаем ученика, который хорошо учится, дисциплинирован, помогает в учебе отстающим и, кроме того, участвует в работе научного кружка или занимается спортом, а Ваш Федя….». Что еще собирался сказать учитель? Решение. Введем обозначения высказываний:1) А – «Федя хорошо учится»; 2) В – «Федя дисциплинирован»; 3) С – «Федя помогает в учебе отстающим»; 4) D – «Федя участвует в работе научного кружка»; 5) E – «Федя занимается спортом». Теперь утверждение «Федя – хороший ученик», согласно «определению» хорошего ученика, данному учителем, на языке алгебры высказываний можно записать так: Учитель утверждает, что «неверно, что Федя – хороший ученик», то есть он утверждает, что Преобразуем выражение, стоящее в левой части этого равенства по правилу де-Моргана: Федин отец утверждает (и учитель согласился с ним), что 35. Было совершено ограбление. Мегре сообщили, что подозреваются трое бродяг: Луи, Франсуа и Этьен. Бродяги дали следующие показания: Луи: Чтобы обвинить меня, достаточно доказать, что Франсуа участвует в ограблении только тогда, когда в нем участвует Этьен, но я не виновен. Франсуа: если Луи невиновен, то, чтобы обвинить меня, достаточно признать Этьена тоже невиновным. Но Этьен виновен тогда и только тогда, когда виновен Луи. А если Этьен виновен, то я не виновен. Этьен: Виновен либо я, либо Франсуа и Луи. Мегре знал, что Этьен всегда лжет, а Луи и Франсуа всегда говорят правду. Это помогло ему распутать дело. Кто был причастен к ограблению? 36. Определить, кто из четырех подозреваемых участвовал в ограблении, если известно, что: 1) если А участвовал, то и В участвовал; 2) если В участвовал,то или участвовал С, или А не участвовал; 3) если D не участвовал, то А участвовал, а С не участвовал; 4) если D участвовал, то А участвовал. 37. Во время допроса каждый из трех подозреваемых сделал следователю три заявления. Валет: Я не виновен; Туза я не знаю; Серый знает, кто это сделал. Хват: Это сделал не я; с Серым я не знаком; это сделал Туз. Туз: Я не виновен; это сделал Серый; Хват лжет, это сделал не я. Серый: Я не виновен; это сделал Валет; Хват может за меня поручиться. При перекрестном допросе каждый из них признал, что из трех сделанных им заявлений два верных и одно неверное. Определите преступника на основании полученной информации. 38. Шестеро подозреваемых в преступлении давали показания. А: «Е виновен». Б: «А лжет и я не виновен». В: «Виновны А или Е, а возможно и оба». Г: «В говорит правду». Д: «В и Е — оба лгут». Е: «Я не виновен». Если правду сказал один и только один из подозреваемых, то кто совершил преступление? 39. Четыре ученицы: Мария, Нина, Ольга и Полина участвовали в соревнованиях и заняли первые четыре места. На вопрос, кто из них какое место занял, три девушки ответили: 1) Ольга была вторая, Полина – третья; 2) Ольга была первая, Нина – вторая; 3) Мария была вторая, Полина – четвертая. В каждом из этих трех ответов одна часть верна, а другая неверна (какая именно часть верна – неизвестно). Какое место заняла каждая из девушек? 40. При составлении расписания на определенный день в определенном классе преподавателями были высказаны просьбы: 1) математик желает иметь первый или второй урок; 2) историк желает иметь первый или третий урок; 3) литератор желает иметь второй или третий урок. Как удовлетворить всем пожеланиям и можно ли это сделать одним способом? 41. Составленная перед концертом программа выступления была потеряна. О порядке следования номеров сохранилась лишь следующая информация: танцоры должны выступать или вторыми, или третьими; музыканты – первыми или вторыми, певцы – первыми или третьими. Какой порядок следования номеров был в потерянной программе? 42. Четыре марсианки, оказавшиеся на Земле в 2... году, на вопрос о их возрасте дали ответы: 1) Ми –22 года, Ме –21 год; 2) Мо –19 лет, Ми –21 год; 3) Ма – 21 год, Мо –18 лет. Известно, что все марсианки – разных возрастов, причем только данных: 18, 19, 21 и 22 и что в каждом ответе одна часть верна, а другая неверна. Сколько лет каждой девушке? 43. Аня, Варя и Клава пошли на дискотеку. Одна из них была в красном платье, другая – в белом, третья – в синем. На вопрос, какое платье было на каждой из девушек, они дали такой ответ: Аня была в красном, Варя – не в красном, Клава – в не синем. В этом условном ответе из трех частей одна верна, две неверны. В каком платье была каждая из девушек? 44. Три брата имеют звание капитана, старшины и сержанта. Из трех утверждений “Алексей старшина”, “Владимир не старшина”, “Семен не сержант” лишь одно верно. Какие воинские звания у братьев? 45. Написав контрольную работу по математике, сестры сообщили своим родителям: Света: На этот раз я написала на 5. Люда: Я написала не на 3. Ира: Я написала не на 5. После проверки работ оказалось, что сестры получили
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 784; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.104.171 (0.016 с.) |

 (читается «не а», «неверно, что а»), которое истинно тогда и только тогда, когда а ложно.
(читается «не а», «неверно, что а»), которое истинно тогда и только тогда, когда а ложно.

 и
и 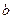 называется такое высказывание
называется такое высказывание  (читается «а и b», «а конъюнкция b»), которое истинно тогда и только тогда, когда истинны оба высказывания а и b.
(читается «а и b», «а конъюнкция b»), которое истинно тогда и только тогда, когда истинны оба высказывания а и b. для обозначения операции конъюнкции может использоваться знак &.
для обозначения операции конъюнкции может использоваться знак &. (читается «а или b», «а дизъюнкция b»), которое истинно тогда и только тогда, когда истинно хотя бы одно из высказываний а или b.
(читается «а или b», «а дизъюнкция b»), которое истинно тогда и только тогда, когда истинно хотя бы одно из высказываний а или b.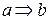 (читается «если а, то b», «из а следует b», «а влечет b», «а имплицирует b»), которое ложно тогда и только тогда, когда высказывание а истинно, а b ложно.
(читается «если а, то b», «из а следует b», «а влечет b», «а имплицирует b»), которое ложно тогда и только тогда, когда высказывание а истинно, а b ложно.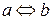 (читается «а тогда и только тогда, когда b», «а необходимо и достаточно для b», «а эквиваленция b»), которое истинно тогда и только тогда, когда истинностные значения a и b совпадают.
(читается «а тогда и только тогда, когда b», «а необходимо и достаточно для b», «а эквиваленция b»), которое истинно тогда и только тогда, когда истинностные значения a и b совпадают. ,
, 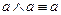 – законы идемпотентности;
– законы идемпотентности; ,
, 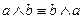 – законы коммутативности;
– законы коммутативности; ,
,  – законы ассоциативности;
– законы ассоциативности; ,
,  –
– ,
, 
 – законы де Моргана;
– законы де Моргана; ,
,  – закон исключенного
– закон исключенного ,
,  – законы поглощения 0 и 1;
– законы поглощения 0 и 1;
 – закон двойного отрицания;
– закон двойного отрицания; ;
;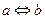 º (
º ( ).
). ,
,  .
.
 .
. не превосходит число7.
не превосходит число7. , 2)
, 2)  , 3) a
, 3) a  .
.
 , 2)
, 2)  , 3)
, 3)  , 4)
, 4) 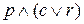 , 5)
, 5) 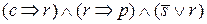 .
. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
. . Построим его отрицание:
. Построим его отрицание: .
. истинна. Что можно сказать о значении истинности высказываний a, b и c?
истинна. Что можно сказать о значении истинности высказываний a, b и c? ложна. Что можно сказать о значении истинности самих высказываний a, b и c?
ложна. Что можно сказать о значении истинности самих высказываний a, b и c?



 ; 2)
; 2)  ; 3)
; 3) 


 ;
; ; 6) (
; 6) (
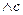 ; 7)
; 7) 
 ;
; 10)
10) 
 ; 12)
; 12) 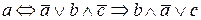 .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. ; 2)
; 2)  .
. ); 2)
); 2)  .
. и
и  ; 2)
; 2)  и
и  ;
; и
и  .
. ; б)
; б)  ;
; .
. .
. ;
;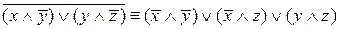 ;
;
 ;
;



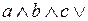
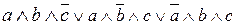 и
и  .
. ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
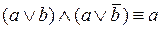 ;
;
 ;
;
 ;
;
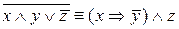 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
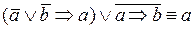 ;
;
 ;
;

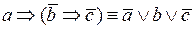 ;
;

 ;
;
 от n переменных можно представить в виде формулы алгебры высказываний.
от n переменных можно представить в виде формулы алгебры высказываний. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  , где n, m, k,r – любыt натуральные числа.
, где n, m, k,r – любыt натуральные числа.
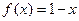 ; б)
; б)  ;
; ; г)
; г)  ;
; ; е)
; е)  ;
; ;з)
;з) 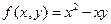 ;
; .
.
 .
. ; 2)
; 2) 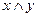 ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  ; 6)
; 6) 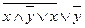
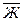 Ú
Ú 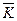 Ù Ж,
Ù Ж, Ú
Ú 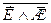 ).
).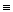 1..
1..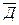
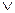 К Ù
К Ù 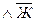 Ú
Ú 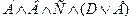
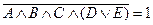 .
. 
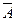


 = 1.
= 1. , а также
, а также 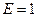 (Федя – лучший лыжник класса). Тогда в полученном равенстве первое и последнее слагаемые ложны, поэтому оно равносильно условию
(Федя – лучший лыжник класса). Тогда в полученном равенстве первое и последнее слагаемые ложны, поэтому оно равносильно условию 


