
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кванторы общности и существованияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте При изучении высказывательных форм (предикатов) был указан один из способов получения высказываний: подстановка какого-нибудь значения переменной в Р(х) из некоторого множества А. Например, Р(х):” х - простое число”. Подставив х = 7, получим высказывание “ 7 - простое число”. Мы познакомимся ещё с двумя логическими операциями: навешивание квантора общности и квантора существования, которые позволяют получить из высказывательных форм высказывания. Подставим перед высказывательной формой Р(х) слово “любое”: “ любое х - простое число”. Получили ложное высказывание. Подставим перед Р(х) слово “некоторые”: “ некоторые числа х - простые”. Получили истинное высказывание. В математике слова “любые”, “некоторые” и их синонимы называются кванторами, которые соответственно называются квантор общности (") и квантор существования ($). Квантор общности заменяется в словесных формулировках словами: любой, все, каждый, всякий и т.д. Квантор существования в словесной формулировке заменяется словами: существует, хотя бы один, какой-нибудь найдётся и т.д. Пусть Р(х) - высказывательная форма на М. Запись ("хÎМ) Р(х) означает: для любого элемента х (из множества М) имеет место Р(х), что уже представляет собой высказывание. Чтобы доказать, что высказывание ("х)Р(х) - истинно, надо перебрать все элементы а, b, с и т.д. из М и убедиться, что Р(а), Р(b), Р(с),... истинны, и, если невозможно перебрать элементы М, должны доказать с помощью рассуждений, что для любого а из М высказывание Р(а) истинно. Чтобы убедиться, что ("х)Р(х) ложно, достаточно найти лишь один элемент аÎМ, для которого Р(а) ложно. ПРИМЕР. Дана высказывательная форма В(х):” В(1): 22 + 1 = 5 - простое число; В(2): В(3): В(4): Можно ли сказать, что ("х)В(х)? Это необходимо доказывать. Леонард Эйлер доказал, что В(5) - ложно, т.е. ПРИМЕР. Рассмотрим высказывание ("х)С(х), где на N задано С(х): “х3 + 5х делится на 6”. Очевидно, С(1), С(2), С(3), С(4) истинны. Но если мы проверим даже миллион значений х всегда есть опасность, что для миллион первого значения х утверждение С(х) окажется ложным. Доказать можно, например, так: х3 + 5х = х3 - х + 6х = х(х2 - 1) + 6х = (х - 1)х(х + 1) + 6х Выражение (х - 1)х(х + 1) делится на 3, так как из трех последовательных натуральных чисел по крайней мере одно делится на 3; это выражение делится и на 2, так как из трех последовательных чисел одно или два числа чётны. Второе слагаемое 6х делится на 6, следовательно и вся сумма делится на 6, т.е. ("х)С(х) - истинно. Пусть С(х) некоторая высказывательная форма. Запись ($х)С(х) означает: существует элемент х из множества М, для которого имеет место С(х). ($х)С(х) уже высказывание. Если во множестве М можно найти элемент а, для которого С(а) истинно, то высказывание($х)С(х) - истинно. Если же в М нет ни одного элемента а, для которого С(а) истинно, высказывание ($х)С(х) - ложно. ПРИМЕР. На множестве N задано С(х):”
ПРИМЕР. На множестве N задано К(х):” х2 + 2х + 3 делится на 7”. К(1) = 6, 6 не делится на 7; К(2) = 11, 11 не делится на 7 и т.д. Гипотеза: ($х)К(х) - ложно. Докажем это. Любое натуральное число по теореме о делении с остатком можно представить в виде n = 7q + r, где r < 7. n2 + 2n + 3 = (7q + r)2 + 2(7q + r) + 3 = 7(7q2 + 2qr + 2q) + r2 + 2r + 3. Итак, число n2 + 2n + 3 делится на 7 тогда и только тогда, когда r2 + 2r + 3 делится на 7. Остаток r Î { 0, 1, 2, 3, 4, 5, 6 }. Методом перебора убедимся, что r2 + 2r + 3 не делится на 7. Итак, ($х)К(х) - ложно.
Как построить отрицание высказывания с квантором? Для того чтобы построить отрицание высказывания с квантором, нужно заменить квантор общности (") на квантор существования ($) и, наоборот, квантор существования на квантор общности, а предложение, стоящее после квантора, на его отрицание, т.е.
Например, пусть даны два высказывания: А: “каждое простое число нечётно”; В: “ каждое простое число чётно”. Будет ли В отрицанием высказывания А? Нет, так как ни одно из высказываний не является истинным. В данном случае
В дальнейшем считаем, что построено отрицание предложения, если не просто записано его отрицание, но и полученное предложение преобразовано к виду, где знаки отрицания стоят перед более простыми выражениями. Например, отрицанием предложения вида А Ù Пусть А(х,у) - высказывательная форма с двумя переменными. Тогда ("х)А(х,у), ($х)А(х,у), ("х)А(х,у), ($х)А(х,у) тоже высказывательные формы но уже с одной переменной. В этом случае говорят, что квантор связывает одну переменную. Чтобы получить из высказывательной формы А(х,у) высказывание необходимо связать обе переменные. Например, ("х)($у)А(х,у) - высказывание. Для высказывательной формы Р(х,у): “ x < y”, заданной на Z, рассмотрим все случаи получения высказывания путем добавления (навешивания) кванторов: 1) ("х)("у)Р(х,у) Û л - “ Для всякого х и для всякого у х < y”; 2) ("у)("х)(х < y) Û л - “Для всякого у и для всякого х х < y”; 3) ($x)($y) (x < y) Û и - “Существует х и существует у такие, что x < y”; 4) ($у)($х) (х < y) Û и - “Существует х и существует у такие, что x < y”; 5) ("х)($у) (x < y) Û и - “Для всякого х существует у такое, что x < y”; 6) ($у)("х) (x < y) Û л - “Существует у такое, что для всякого х х < y”; 7) ("у)($х) (х < y) Û и - “Для всякого у существует х такое, что x < y”; 8) ($х)("у) (x < y) Û л - “Существует x такое, что для всякого y х < y”. ` Обратите внимание на высказывания (1) и (2), (3) и (4). Структуры этих высказываний отличаются лишь порядком следования одноименных кванторов, но при этом не меняются смысл и значения истинности высказываний. Высказывания (5) и (6), (7) и (8) отличаются порядком следования разноимённых кванторов, что приводит к изменению смысла и, возможно, значения истинности высказывания. Высказывание (7) утверждает о наличии в Z наименьшего числа, что ложно. (8) утверждает об отсутствии такого, что истинно. Теоретические вопросы: 1. Понятие предиката от одного, нескольких переменных. 2. Примеры одноместных и двуместных предикатов. 3. Область истинности предиката. 4. Кванторы общности и существования. Свободные и связанные переменные. Операции над предикатами. Какова область истинности 5. Преобразование формул логики предикатов. Определение тождественно истинного и тождественно ложного предиката, связь с областью истинности. Основные равносильности. Упражнения 5.1. Укажите несколько значений переменных, при которых следующие предикаты истинны, ложны: 1. х 2. х < 1, x Î N; 10. 3. x > 6® x ³ 3, xÎZ; 11. sin x = - 4. x 5. 6. | x - 5 | < 2, 14. x + y < 3, x,yÎ N; 7. | 2x + 3 | ³ 2x + 3, x Î R; 15. x (y - 1) = 0, x,yÎR; 8.
5.2. Найдите область истинности предикатов упражнения 5.1. Случаи 13 - 16 изобразите на координатной плоскости.
5.3. Найдите область истинности предикатов: 1. 2. 3. 4. 5. 6.
5.4. Найдите область истинности предикатов: 1. ( 2. ( 3.( 4.( 5.((x+3) 6.((x 7.(1 + 8.( 9.( 10.(0,2 (2x - 3) < x - 2) Ú (5x - 7 > x - 6).
5.5. Найдите область истинности предикатов: 1. sin x = 3. tg x = 1; 4. ctg x = - 1; 5. 4 - cos 5.6. Определите тождественную истинность и тождественную ложность предикатов: 1. x 3. 1+cos x=2 cos 5. (x 7. (x
5.7. Найдите значение следующих высказываний: 1. (" x Î N) (x £ 1); 2. ($ x Î N) x £ 1 3. (" x Î Z) (x 5. (" x Î Z) ((x > 10) ®(x ³ 3)); 6. (" x Î Z) ((x ³ 3) ® (x > 10); 7. (" x,y Î Z) (x + y = 3); 8. ($ x,y Î Z) (x + y = 3); 9. (" x,y Î R) (x < y ® x 10. (" x,y Î R
З А Н Я Т И Е № 6.
Применение предикатов.
|
||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 3008; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 - простое число”.
- простое число”.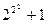 = 17 - простое число;
= 17 - простое число; = 257 - простое число;
= 257 - простое число; = 65537 - простое число.
= 65537 - простое число.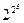 + 1 = 232 + 1 делится на 641 и, следовательно, ("х)В(х) - ложно.
+ 1 = 232 + 1 делится на 641 и, следовательно, ("х)В(х) - ложно. ”. С(1) - ложно, С(2) - ложно, С(5) - истинно. Следовательно, ($х)С(х) - истинное высказывание.
”. С(1) - ложно, С(2) - ложно, С(5) - истинно. Следовательно, ($х)С(х) - истинное высказывание. [("x)P(x) Û ($x)
[("x)P(x) Û ($x)  ;
;  ;
;  ;
;  ? Дать геометрические интерпретации.
? Дать геометрические интерпретации. 2, х Î N; 9.
2, х Î N; 9.  = - x, x Î R;
= - x, x Î R; > 0,
> 0, , xÎ R;
, xÎ R; + 3x +6 = 0, x Î R; 12. cos x =
+ 3x +6 = 0, x Î R; 12. cos x =  , x ÎR;
, x ÎR;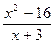 = 0, xÎR; 13. x ³ y, x,y Î R;
= 0, xÎR; 13. x ³ y, x,y Î R; = 0; 7. | 3x - 2 | > 8;
= 0; 7. | 3x - 2 | > 8; =
=  ; 8. | 5x - 3 | < 7;
; 8. | 5x - 3 | < 7; -
- 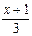 >
>  ; 9. 2 - | x | = 1,7;
; 9. 2 - | x | = 1,7; ; 10. | 3x - 1 | = 3x - 1;
; 10. | 3x - 1 | = 3x - 1; < 0; 11. | 3x - 1 | = 1 - 3x;
< 0; 11. | 3x - 1 | = 1 - 3x; > 0; 12. | 2x + 4 | ³ 2x + 4.
> 0; 12. | 2x + 4 | ³ 2x + 4. < x + 1,5) Ù (2x - 8 > 3 - 0,5 x);
< x + 1,5) Ù (2x - 8 > 3 - 0,5 x); - 4 <
- 4 <  - 1) Ù (
- 1) Ù ( x + 2 (2x- 1) < 3(x +1);
x + 2 (2x- 1) < 3(x +1); -
-  +2x<3x-3) Ù (
+2x<3x-3) Ù ( - 3(1-x)+2x<
- 3(1-x)+2x<  );
); -
- 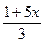 + x < 2x - 4)Ù(
+ x < 2x - 4)Ù( + 3 (x - 1)<
+ 3 (x - 1)<  );
); £
£  ) Ú (- 1 < 5x - 5)
) Ú (- 1 < 5x - 5) -
-  > 2) Ú (- 3x - 1 > 2);
> 2) Ú (- 3x - 1 > 2); + 6x >
+ 6x >  + 4) Ú (
+ 4) Ú ( -
-  >
> 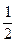 -
-  );
); ; 2. cos x = -
; 2. cos x = -  ;
; sin
sin 
 ; xÎR; 4. 1- cos x=2 sin
; xÎR; 4. 1- cos x=2 sin  2, xÎZ; 6.(x
2, xÎZ; 6.(x  9. (x
9. (x 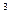 < y
< y  ) (x < y ® x
) (x < y ® x 


